A neural network approach for solving the Monge-Ampère equation with transport boundary condition

This paper introduces a novel neural network-based approach to solving the Monge-Amp\`ere equation with the transport boundary condition, specifically targeted towards optical design applications. We leverage multilayer perceptron networks to learn approximate solutions by minimizing a loss function that encompasses the equation's residual, boundary conditions, and convexity constraints. Our main results demonstrate the efficacy of this method, optimized using L-BFGS, through a series of test cases encompassing symmetric and asymmetric circle-to-circle, square-to-circle, and circle-to-flower reflector mapping problems. Comparative analysis with a conventional least-squares finite-difference solver reveals the competitive, and often superior, performance of our neural network approach on the test cases examined here. A comprehensive hyperparameter study further illuminates the impact of factors such as sampling density, network architecture, and optimization algorithm. While promising, further investigation is needed to verify the method's robustness for more complicated problems and to ensure consistent convergence. Nonetheless, the simplicity and adaptability of this neural network-based approach position it as a compelling alternative to specialized partial differential equation solvers.

A Simple and Efficient Stochastic Rounding Method for Training Neural Networks in Low Precision

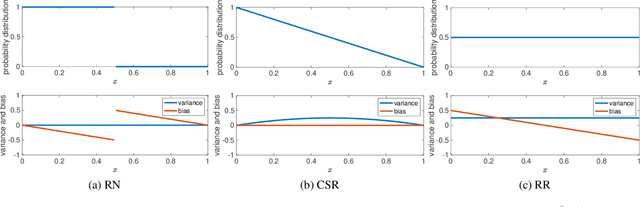
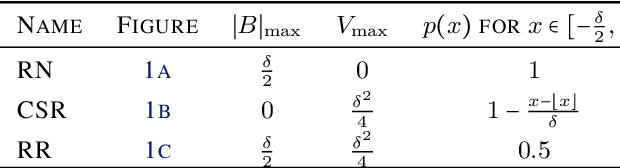
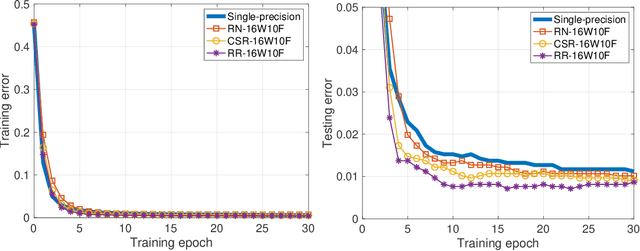
Conventional stochastic rounding (CSR) is widely employed in the training of neural networks (NNs), showing promising training results even in low-precision computations. We introduce an improved stochastic rounding method, that is simple and efficient. The proposed method succeeds in training NNs with 16-bit fixed-point numbers and provides faster convergence and higher classification accuracy than both CSR and deterministic rounding-to-the-nearest method.

Improved stochastic rounding

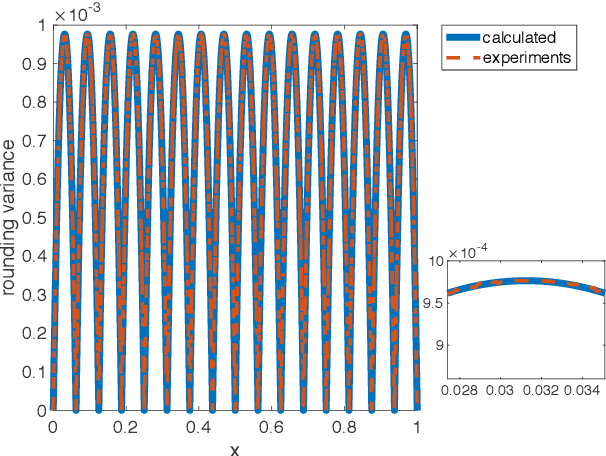
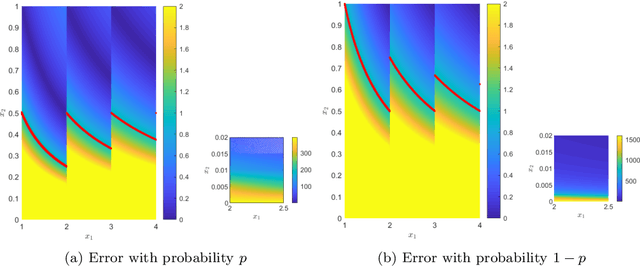
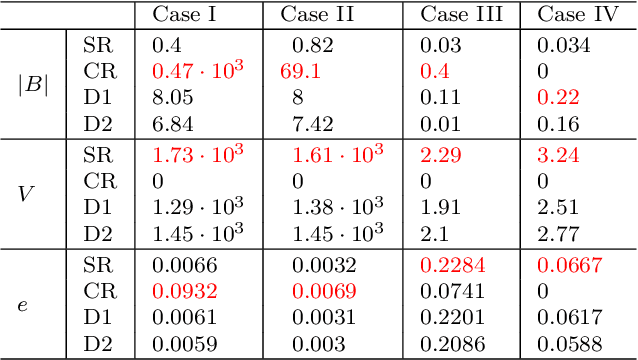
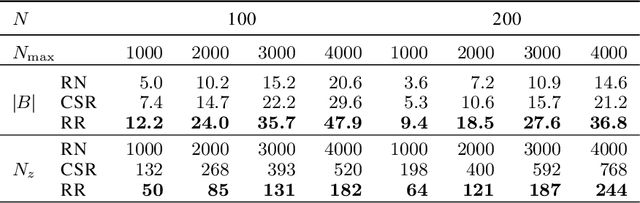
Due to the limited number of bits in floating-point or fixed-point arithmetic, rounding is a necessary step in many computations. Although rounding methods can be tailored for different applications, round-off errors are generally unavoidable. When a sequence of computations is implemented, round-off errors may be magnified or accumulated. The magnification of round-off errors may cause serious failures. Stochastic rounding (SR) was introduced as an unbiased rounding method, which is widely employed in, for instance, the training of neural networks (NNs), showing a promising training result even in low-precision computations. Although the employment of SR in training NNs is consistently increasing, the error analysis of SR is still to be improved. Additionally, the unbiased rounding results of SR are always accompanied by large variances. In this study, some general properties of SR are stated and proven. Furthermore, an upper bound of rounding variance is introduced and validated. Two new probability distributions of SR are proposed to study the trade-off between variance and bias, by solving a multiple objective optimization problem. In the simulation study, the rounding variance, bias, and relative errors of SR are studied for different operations, such as summation, square root calculation through Newton iteration and inner product computation, with specific rounding precision.