On the influence of roundoff errors on the convergence of the gradient descent method with low-precision floating-point computation

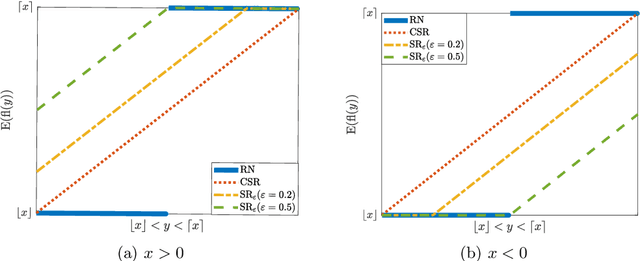
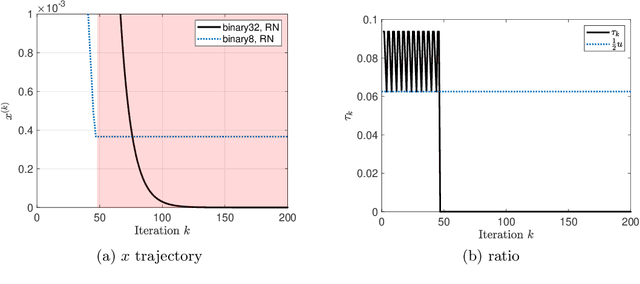
The employment of stochastic rounding schemes helps prevent stagnation of convergence, due to vanishing gradient effect when implementing the gradient descent method in low precision. Conventional stochastic rounding achieves zero bias by preserving small updates with probabilities proportional to their relative magnitudes. In this study, we propose a new stochastic rounding scheme that trades the zero bias property with a larger probability to preserve small gradients. Our method yields a constant rounding bias that, at each iteration, lies in a descent direction. For convex problems, we prove that the proposed rounding method has a beneficial effect on the convergence rate of gradient descent. We validate our theoretical analysis by comparing the performances of various rounding schemes when optimizing a multinomial logistic regression model and when training a simple neural network with 8-bit floating-point format.

A Simple and Efficient Stochastic Rounding Method for Training Neural Networks in Low Precision

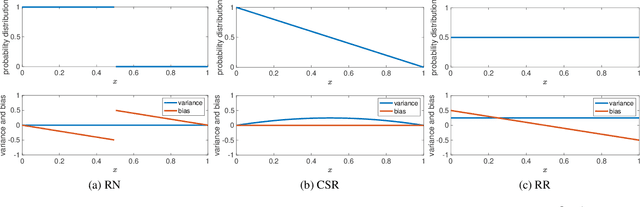
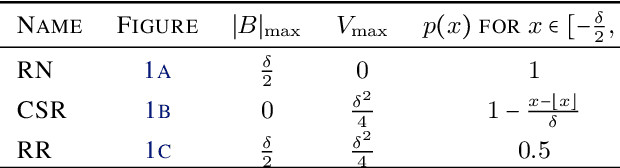
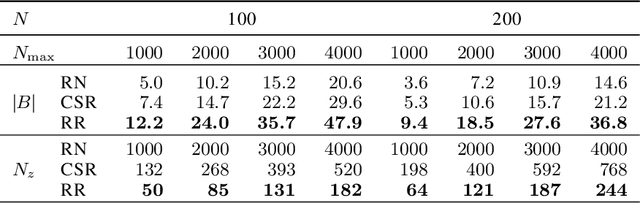
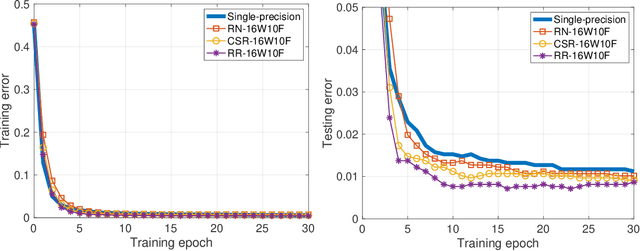
Conventional stochastic rounding (CSR) is widely employed in the training of neural networks (NNs), showing promising training results even in low-precision computations. We introduce an improved stochastic rounding method, that is simple and efficient. The proposed method succeeds in training NNs with 16-bit fixed-point numbers and provides faster convergence and higher classification accuracy than both CSR and deterministic rounding-to-the-nearest method.

Improved stochastic rounding

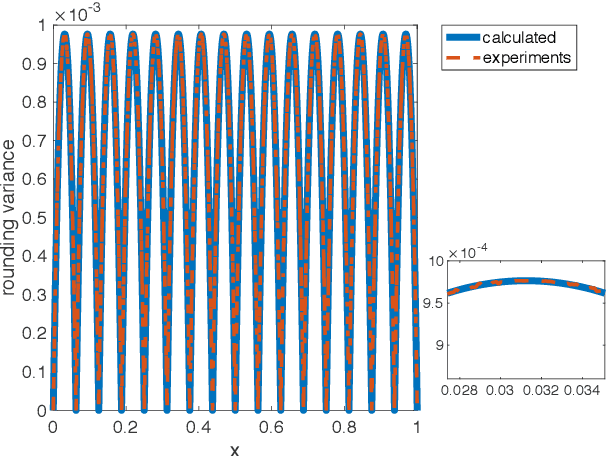
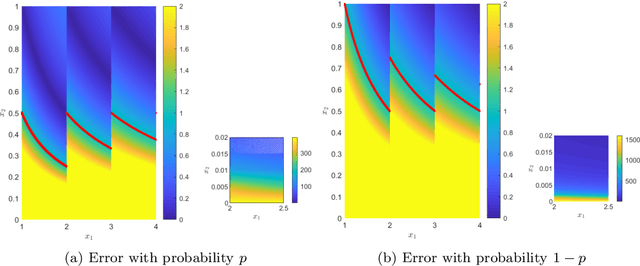
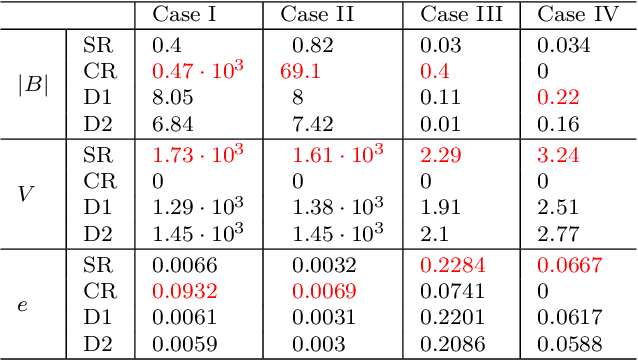
Due to the limited number of bits in floating-point or fixed-point arithmetic, rounding is a necessary step in many computations. Although rounding methods can be tailored for different applications, round-off errors are generally unavoidable. When a sequence of computations is implemented, round-off errors may be magnified or accumulated. The magnification of round-off errors may cause serious failures. Stochastic rounding (SR) was introduced as an unbiased rounding method, which is widely employed in, for instance, the training of neural networks (NNs), showing a promising training result even in low-precision computations. Although the employment of SR in training NNs is consistently increasing, the error analysis of SR is still to be improved. Additionally, the unbiased rounding results of SR are always accompanied by large variances. In this study, some general properties of SR are stated and proven. Furthermore, an upper bound of rounding variance is introduced and validated. Two new probability distributions of SR are proposed to study the trade-off between variance and bias, by solving a multiple objective optimization problem. In the simulation study, the rounding variance, bias, and relative errors of SR are studied for different operations, such as summation, square root calculation through Newton iteration and inner product computation, with specific rounding precision.