AdamL: A fast adaptive gradient method incorporating loss function

Adaptive first-order optimizers are fundamental tools in deep learning, although they may suffer from poor generalization due to the nonuniform gradient scaling. In this work, we propose AdamL, a novel variant of the Adam optimizer, that takes into account the loss function information to attain better generalization results. We provide sufficient conditions that together with the Polyak-Lojasiewicz inequality, ensure the linear convergence of AdamL. As a byproduct of our analysis, we prove similar convergence properties for the EAdam, and AdaBelief optimizers. Experimental results on benchmark functions show that AdamL typically achieves either the fastest convergence or the lowest objective function values when compared to Adam, EAdam, and AdaBelief. These superior performances are confirmed when considering deep learning tasks such as training convolutional neural networks, training generative adversarial networks using vanilla convolutional neural networks, and long short-term memory networks. Finally, in the case of vanilla convolutional neural networks, AdamL stands out from the other Adam's variants and does not require the manual adjustment of the learning rate during the later stage of the training.

On the Convergence of the Gradient Descent Method with Stochastic Fixed-point Rounding Errors under the Polyak-Lojasiewicz Inequality

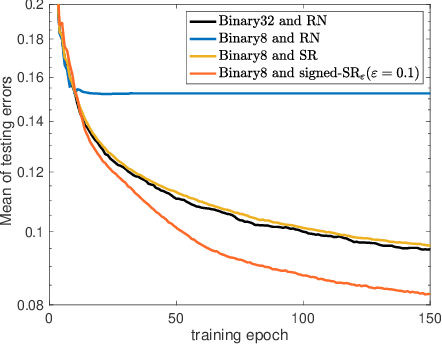
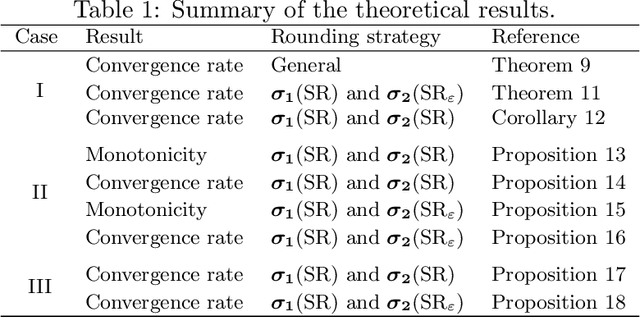
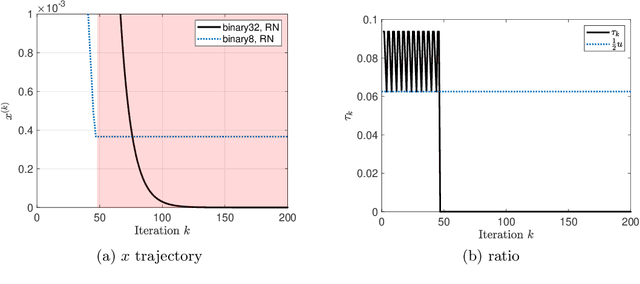
When training neural networks with low-precision computation, rounding errors often cause stagnation or are detrimental to the convergence of the optimizers; in this paper we study the influence of rounding errors on the convergence of the gradient descent method for problems satisfying the Polyak-Lojasiewicz inequality. Within this context, we show that, in contrast, biased stochastic rounding errors may be beneficial since choosing a proper rounding strategy eliminates the vanishing gradient problem and forces the rounding bias in a descent direction. Furthermore, we obtain a bound on the convergence rate that is stricter than the one achieved by unbiased stochastic rounding. The theoretical analysis is validated by comparing the performances of various rounding strategies when optimizing several examples using low-precision fixed-point number formats.

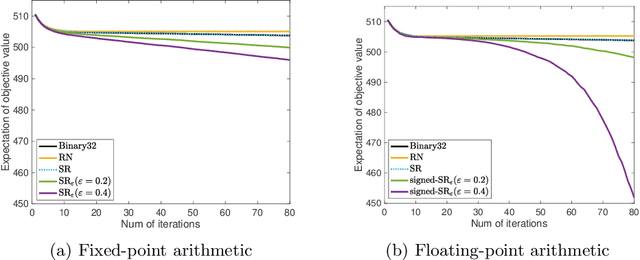
On the influence of roundoff errors on the convergence of the gradient descent method with low-precision floating-point computation

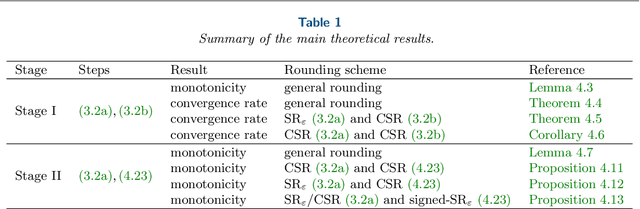
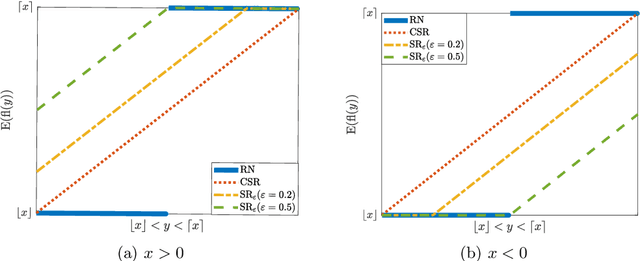
The employment of stochastic rounding schemes helps prevent stagnation of convergence, due to vanishing gradient effect when implementing the gradient descent method in low precision. Conventional stochastic rounding achieves zero bias by preserving small updates with probabilities proportional to their relative magnitudes. In this study, we propose a new stochastic rounding scheme that trades the zero bias property with a larger probability to preserve small gradients. Our method yields a constant rounding bias that, at each iteration, lies in a descent direction. For convex problems, we prove that the proposed rounding method has a beneficial effect on the convergence rate of gradient descent. We validate our theoretical analysis by comparing the performances of various rounding schemes when optimizing a multinomial logistic regression model and when training a simple neural network with 8-bit floating-point format.

Certified and fast computations with shallow covariance kernels

Many techniques for data science and uncertainty quantification demand efficient tools to handle Gaussian random fields, which are defined in terms of their mean functions and covariance operators. Recently, parameterized Gaussian random fields have gained increased attention, due to their higher degree of flexibility. However, especially if the random field is parameterized through its covariance operator, classical random field discretization techniques fail or become inefficient. In this work we introduce and analyze a new and certified algorithm for the low-rank approximation of a parameterized family of covariance operators which represents an extension of the adaptive cross approximation method for symmetric positive definite matrices. The algorithm relies on an affine linear expansion of the covariance operator with respect to the parameters, which needs to be computed in a preprocessing step using, e.g., the empirical interpolation method. We discuss and test our new approach for isotropic covariance kernels, such as Mat\'ern kernels. The numerical results demonstrate the advantages of our approach in terms of computational time and confirm that the proposed algorithm provides the basis of a fast sampling procedure for parameter dependent Gaussian random fields.