How to beat a Bayesian adversary

Deep neural networks and other modern machine learning models are often susceptible to adversarial attacks. Indeed, an adversary may often be able to change a model's prediction through a small, directed perturbation of the model's input - an issue in safety-critical applications. Adversarially robust machine learning is usually based on a minmax optimisation problem that minimises the machine learning loss under maximisation-based adversarial attacks. In this work, we study adversaries that determine their attack using a Bayesian statistical approach rather than maximisation. The resulting Bayesian adversarial robustness problem is a relaxation of the usual minmax problem. To solve this problem, we propose Abram - a continuous-time particle system that shall approximate the gradient flow corresponding to the underlying learning problem. We show that Abram approximates a McKean-Vlasov process and justify the use of Abram by giving assumptions under which the McKean-Vlasov process finds the minimiser of the Bayesian adversarial robustness problem. We discuss two ways to discretise Abram and show its suitability in benchmark adversarial deep learning experiments.

A Learnable Prior Improves Inverse Tumor Growth Modeling

Biophysical modeling, particularly involving partial differential equations (PDEs), offers significant potential for tailoring disease treatment protocols to individual patients. However, the inverse problem-solving aspect of these models presents a substantial challenge, either due to the high computational requirements of model-based approaches or the limited robustness of deep learning (DL) methods. We propose a novel framework that leverages the unique strengths of both approaches in a synergistic manner. Our method incorporates a DL ensemble for initial parameter estimation, facilitating efficient downstream evolutionary sampling initialized with this DL-based prior. We showcase the effectiveness of integrating a rapid deep-learning algorithm with a high-precision evolution strategy in estimating brain tumor cell concentrations from magnetic resonance images. The DL-Prior plays a pivotal role, significantly constraining the effective sampling-parameter space. This reduction results in a fivefold convergence acceleration and a Dice-score of 95%

Subsampling Error in Stochastic Gradient Langevin Diffusions

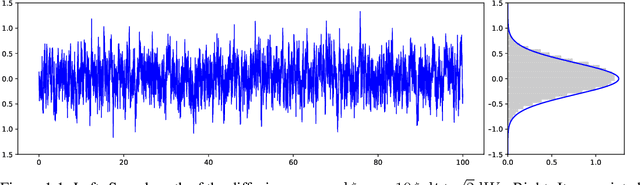
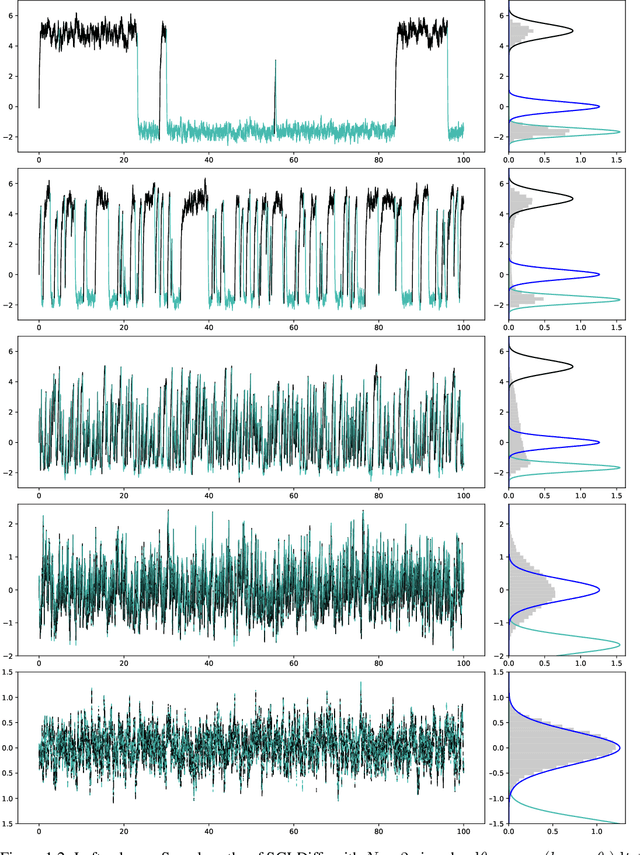
The Stochastic Gradient Langevin Dynamics (SGLD) are popularly used to approximate Bayesian posterior distributions in statistical learning procedures with large-scale data. As opposed to many usual Markov chain Monte Carlo (MCMC) algorithms, SGLD is not stationary with respect to the posterior distribution; two sources of error appear: The first error is introduced by an Euler--Maruyama discretisation of a Langevin diffusion process, the second error comes from the data subsampling that enables its use in large-scale data settings. In this work, we consider an idealised version of SGLD to analyse the method's pure subsampling error that we then see as a best-case error for diffusion-based subsampling MCMC methods. Indeed, we introduce and study the Stochastic Gradient Langevin Diffusion (SGLDiff), a continuous-time Markov process that follows the Langevin diffusion corresponding to a data subset and switches this data subset after exponential waiting times. There, we show that the Wasserstein distance between the posterior and the limiting distribution of SGLDiff is bounded above by a fractional power of the mean waiting time. Importantly, this fractional power does not depend on the dimension of the state space. We bring our results into context with other analyses of SGLD.

Can Physics-Informed Neural Networks beat the Finite Element Method?

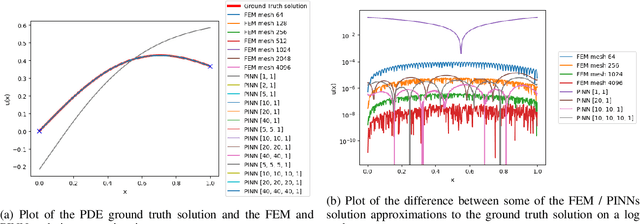
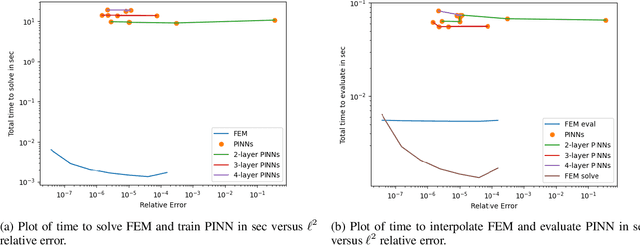
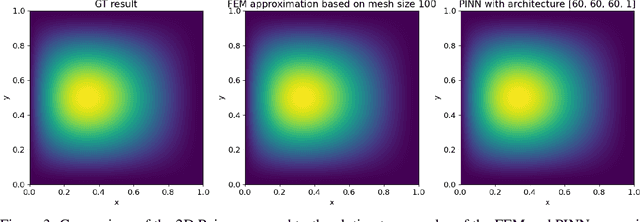
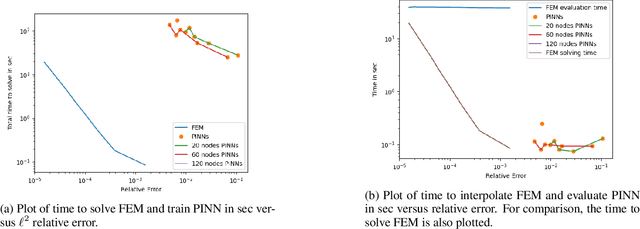
Partial differential equations play a fundamental role in the mathematical modelling of many processes and systems in physical, biological and other sciences. To simulate such processes and systems, the solutions of PDEs often need to be approximated numerically. The finite element method, for instance, is a usual standard methodology to do so. The recent success of deep neural networks at various approximation tasks has motivated their use in the numerical solution of PDEs. These so-called physics-informed neural networks and their variants have shown to be able to successfully approximate a large range of partial differential equations. So far, physics-informed neural networks and the finite element method have mainly been studied in isolation of each other. In this work, we compare the methodologies in a systematic computational study. Indeed, we employ both methods to numerically solve various linear and nonlinear partial differential equations: Poisson in 1D, 2D, and 3D, Allen-Cahn in 1D, semilinear Schr\"odinger in 1D and 2D. We then compare computational costs and approximation accuracies. In terms of solution time and accuracy, physics-informed neural networks have not been able to outperform the finite element method in our study. In some experiments, they were faster at evaluating the solved PDE.

Losing momentum in continuous-time stochastic optimisation

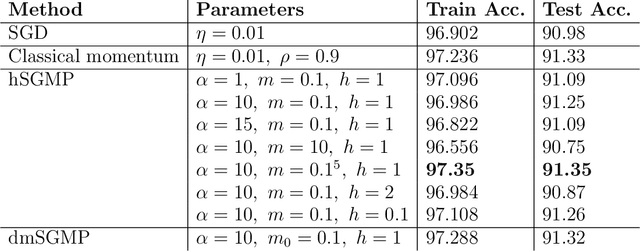
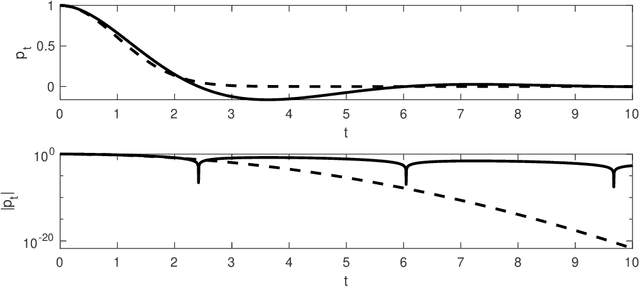
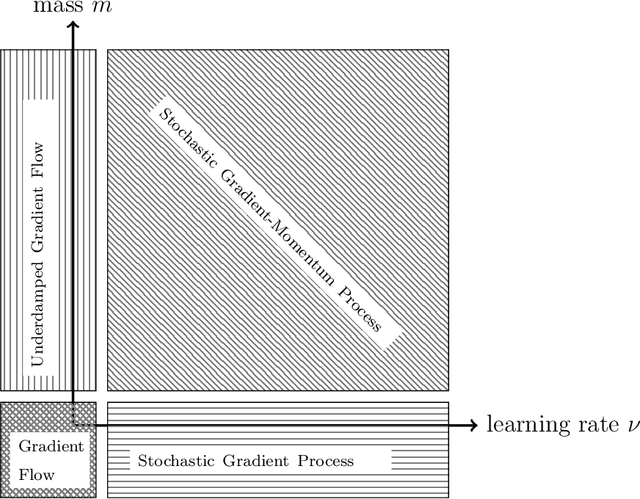
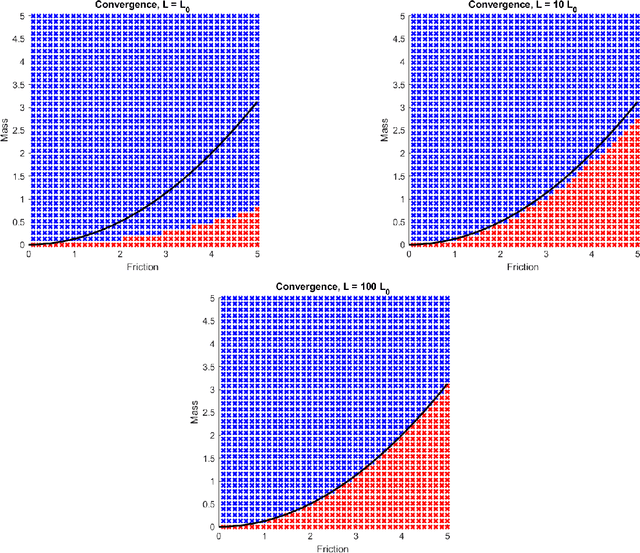
The training of deep neural networks and other modern machine learning models usually consists in solving non-convex optimisation problems that are high-dimensional and subject to large-scale data. Here, momentum-based stochastic optimisation algorithms have become especially popular in recent years. The stochasticity arises from data subsampling which reduces computational cost. Moreover, both, momentum and stochasticity are supposed to help the algorithm to overcome local minimisers and, hopefully, converge globally. Theoretically, this combination of stochasticity and momentum is badly understood. In this work, we propose and analyse a continuous-time model for stochastic gradient descent with momentum. This model is a piecewise-deterministic Markov process that represents the particle movement by an underdamped dynamical system and the data subsampling through a stochastic switching of the dynamical system. In our analysis, we investigate longtime limits, the subsampling-to-no-subsampling limit, and the momentum-to-no-momentum limit. We are particularly interested in the case of reducing the momentum over time: intuitively, the momentum helps to overcome local minimisers in the initial phase of the algorithm, but prohibits fast convergence to a global minimiser later. Under convexity assumptions, we show convergence of our dynamical system to the global minimiser when reducing momentum over time and let the subsampling rate go to infinity. We then propose a stable, symplectic discretisation scheme to construct an algorithm from our continuous-time dynamical system. In numerical experiments, we study our discretisation scheme in convex and non-convex test problems. Additionally, we train a convolutional neural network to solve the CIFAR-10 image classification problem. Here, our algorithm reaches competitive results compared to stochastic gradient descent with momentum.

Joint reconstruction-segmentation on graphs

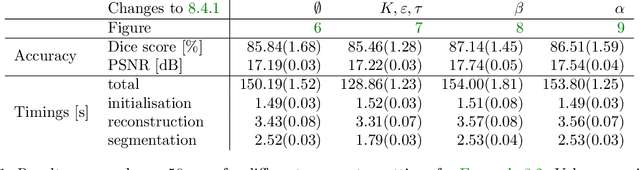
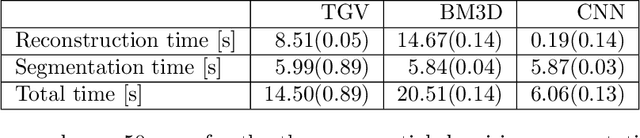
Practical image segmentation tasks concern images which must be reconstructed from noisy, distorted, and/or incomplete observations. A recent approach for solving such tasks is to perform this reconstruction jointly with the segmentation, using each to guide the other. However, this work has so far employed relatively simple segmentation methods, such as the Chan--Vese algorithm. In this paper, we present a method for joint reconstruction-segmentation using graph-based segmentation methods, which have been seeing increasing recent interest. Complications arise due to the large size of the matrices involved, and we show how these complications can be managed. We then analyse the convergence properties of our scheme. Finally, we apply this scheme to distorted versions of ``two cows'' images familiar from previous graph-based segmentation literature, first to a highly noised version and second to a blurred version, achieving highly accurate segmentations in both cases. We compare these results to those obtained by sequential reconstruction-segmentation approaches, finding that our method competes with, or even outperforms, those approaches in terms of reconstruction and segmentation accuracy.

Gradient flows and randomised thresholding: sparse inversion and classification

Sparse inversion and classification problems are ubiquitous in modern data science and imaging. They are often formulated as non-smooth minimisation problems. In sparse inversion, we minimise, e.g., the sum of a data fidelity term and an L1/LASSO regulariser. In classification, we consider, e.g., the sum of a data fidelity term and a non-smooth Ginzburg--Landau energy. Standard (sub)gradient descent methods have shown to be inefficient when approaching such problems. Splitting techniques are much more useful: here, the target function is partitioned into a sum of two subtarget functions -- each of which can be efficiently optimised. Splitting proceeds by performing optimisation steps alternately with respect to each of the two subtarget functions. In this work, we study splitting from a stochastic continuous-time perspective. Indeed, we define a differential inclusion that follows one of the two subtarget function's negative subgradient at each point in time. The choice of the subtarget function is controlled by a binary continuous-time Markov process. The resulting dynamical system is a stochastic approximation of the underlying subgradient flow. We investigate this stochastic approximation for an L1-regularised sparse inversion flow and for a discrete Allen-Cahn equation minimising a Ginzburg--Landau energy. In both cases, we study the longtime behaviour of the stochastic dynamical system and its ability to approximate the underlying subgradient flow at any accuracy. We illustrate our theoretical findings in a simple sparse estimation problem and also in a low-dimensional classification problem.

A Continuous-time Stochastic Gradient Descent Method for Continuous Data

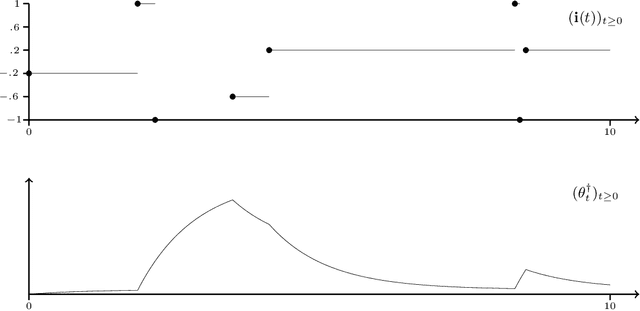
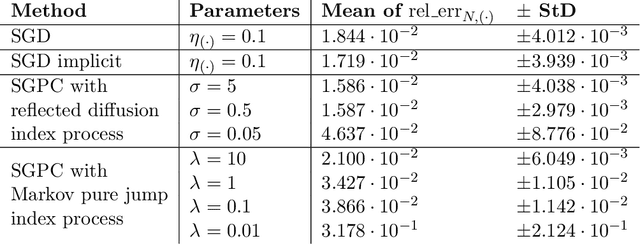
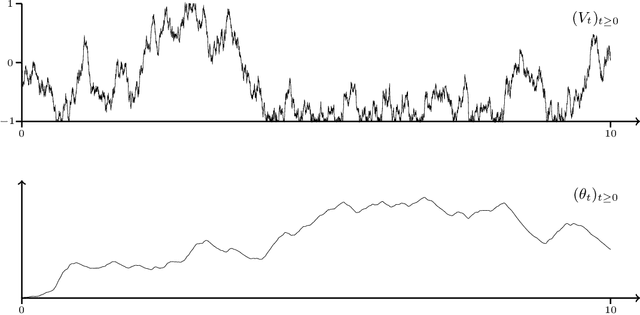
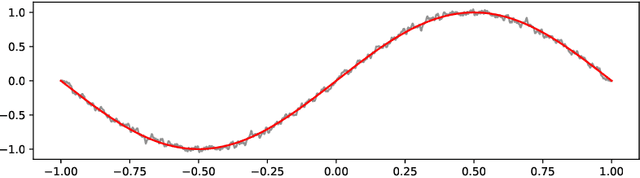
Optimization problems with continuous data appear in, e.g., robust machine learning, functional data analysis, and variational inference. Here, the target function is given as an integral over a family of (continuously) indexed target functions - integrated with respect to a probability measure. Such problems can often be solved by stochastic optimization methods: performing optimization steps with respect to the indexed target function with randomly switched indices. In this work, we study a continuous-time variant of the stochastic gradient descent algorithm for optimization problems with continuous data. This so-called stochastic gradient process consists in a gradient flow minimizing an indexed target function that is coupled with a continuous-time index process determining the index. Index processes are, e.g., reflected diffusions, pure jump processes, or other L\'evy processes on compact spaces. Thus, we study multiple sampling patterns for the continuous data space and allow for data simulated or streamed at runtime of the algorithm. We analyze the approximation properties of the stochastic gradient process and study its longtime behavior and ergodicity under constant and decreasing learning rates. We end with illustrating the applicability of the stochastic gradient process in a polynomial regression problem with noisy functional data, as well as in a physics-informed neural network.

Analysis of Stochastic Gradient Descent in Continuous Time

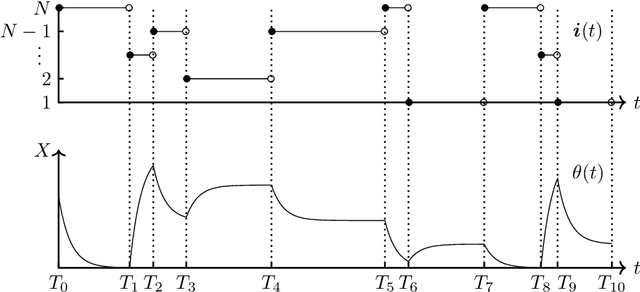
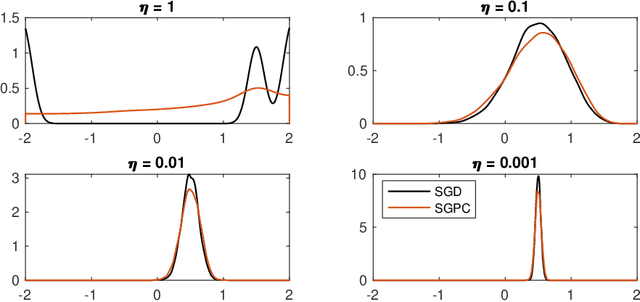
We introduce the stochastic gradient process as a continuous-time representation of the celebrated stochastic gradient descent algorithm. The stochastic gradient process is a dynamical system that is coupled with a continuous-time Markov process living on a finite state space. The dynamical system - a gradient flow - represents the gradient descent part, the process on the finite state space represents the stochastic switching among the data sets. Processes of this type are, for instance, used to model clonal populations in fluctuating environments. After introducing it, we study theoretical properties of the stochastic gradient process. We show that it converges weakly to the gradient flow with respect to the full target function, as the learning rate approaches zero. Moreover, we give assumptions under which the stochastic gradient process is exponentially ergodic. We then additionally assume that the single target functions are strongly convex and the learning rate goes to zero sufficiently slowly. In this case, the process converges weakly at exponential rate to any neighbourhood of the global minimum of the full target function. We conclude with a discussion of discretisation strategies for the stochastic gradient process and illustrate our concepts in numerical experiments.

Certified and fast computations with shallow covariance kernels

Many techniques for data science and uncertainty quantification demand efficient tools to handle Gaussian random fields, which are defined in terms of their mean functions and covariance operators. Recently, parameterized Gaussian random fields have gained increased attention, due to their higher degree of flexibility. However, especially if the random field is parameterized through its covariance operator, classical random field discretization techniques fail or become inefficient. In this work we introduce and analyze a new and certified algorithm for the low-rank approximation of a parameterized family of covariance operators which represents an extension of the adaptive cross approximation method for symmetric positive definite matrices. The algorithm relies on an affine linear expansion of the covariance operator with respect to the parameters, which needs to be computed in a preprocessing step using, e.g., the empirical interpolation method. We discuss and test our new approach for isotropic covariance kernels, such as Mat\'ern kernels. The numerical results demonstrate the advantages of our approach in terms of computational time and confirm that the proposed algorithm provides the basis of a fast sampling procedure for parameter dependent Gaussian random fields.