Normalizing flows as approximations of optimal transport maps via linear-control neural ODEs

The term "Normalizing Flows" is related to the task of constructing invertible transport maps between probability measures by means of deep neural networks. In this paper, we consider the problem of recovering the $W_2$-optimal transport map $T$ between absolutely continuous measures $\mu,\nu\in\mathcal{P}(\mathbb{R}^n)$ as the flow of a linear-control neural ODE. We first show that, under suitable assumptions on $\mu,\nu$ and on the controlled vector fields, the optimal transport map is contained in the $C^0_c$-closure of the flows generated by the system. Assuming that discrete approximations $\mu_N,\nu_N$ of the original measures $\mu,\nu$ are available, we use a discrete optimal coupling $\gamma_N$ to define an optimal control problem. With a $\Gamma$-convergence argument, we prove that its solutions correspond to flows that approximate the optimal transport map $T$. Finally, taking advantage of the Pontryagin Maximum Principle, we propose an iterative numerical scheme for the resolution of the optimal control problem, resulting in an algorithm for the practical computation of the approximated optimal transport map.

A minimax optimal control approach for robust neural ODEs

In this paper, we address the adversarial training of neural ODEs from a robust control perspective. This is an alternative to the classical training via empirical risk minimization, and it is widely used to enforce reliable outcomes for input perturbations. Neural ODEs allow the interpretation of deep neural networks as discretizations of control systems, unlocking powerful tools from control theory for the development and the understanding of machine learning. In this specific case, we formulate the adversarial training with perturbed data as a minimax optimal control problem, for which we derive first order optimality conditions in the form of Pontryagin's Maximum Principle. We provide a novel interpretation of robust training leading to an alternative weighted technique, which we test on a low-dimensional classification task.

From NeurODEs to AutoencODEs: a mean-field control framework for width-varying Neural Networks

In our work, we build upon the established connection between Residual Neural Networks (ResNets) and continuous-time control systems known as NeurODEs. By construction, NeurODEs have been limited to constant-width layers, making them unsuitable for modeling deep learning architectures with width-varying layers. In this paper, we propose a continuous-time Autoencoder, which we call AutoencODE, and we extend to this case the mean-field control framework already developed for usual NeurODEs. In this setting, we tackle the case of low Tikhonov regularization, resulting in potentially non-convex cost landscapes. While the global results obtained for high Tikhonov regularization may not hold globally, we show that many of them can be recovered in regions where the loss function is locally convex. Inspired by our theoretical findings, we develop a training method tailored to this specific type of Autoencoders with residual connections, and we validate our approach through numerical experiments conducted on various examples.

Losing momentum in continuous-time stochastic optimisation

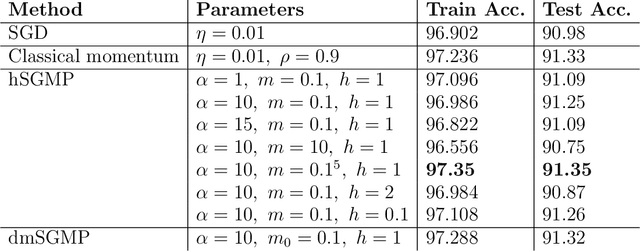
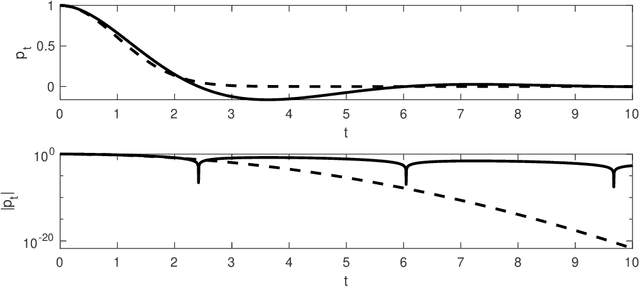
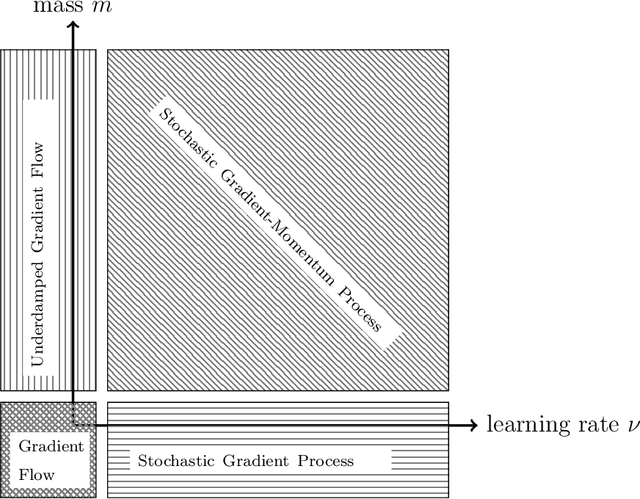
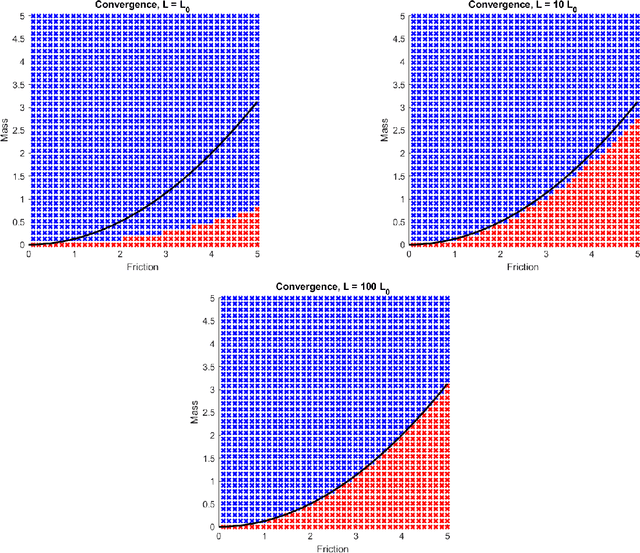
The training of deep neural networks and other modern machine learning models usually consists in solving non-convex optimisation problems that are high-dimensional and subject to large-scale data. Here, momentum-based stochastic optimisation algorithms have become especially popular in recent years. The stochasticity arises from data subsampling which reduces computational cost. Moreover, both, momentum and stochasticity are supposed to help the algorithm to overcome local minimisers and, hopefully, converge globally. Theoretically, this combination of stochasticity and momentum is badly understood. In this work, we propose and analyse a continuous-time model for stochastic gradient descent with momentum. This model is a piecewise-deterministic Markov process that represents the particle movement by an underdamped dynamical system and the data subsampling through a stochastic switching of the dynamical system. In our analysis, we investigate longtime limits, the subsampling-to-no-subsampling limit, and the momentum-to-no-momentum limit. We are particularly interested in the case of reducing the momentum over time: intuitively, the momentum helps to overcome local minimisers in the initial phase of the algorithm, but prohibits fast convergence to a global minimiser later. Under convexity assumptions, we show convergence of our dynamical system to the global minimiser when reducing momentum over time and let the subsampling rate go to infinity. We then propose a stable, symplectic discretisation scheme to construct an algorithm from our continuous-time dynamical system. In numerical experiments, we study our discretisation scheme in convex and non-convex test problems. Additionally, we train a convolutional neural network to solve the CIFAR-10 image classification problem. Here, our algorithm reaches competitive results compared to stochastic gradient descent with momentum.

Deep Learning Approximation of Diffeomorphisms via Linear-Control Systems

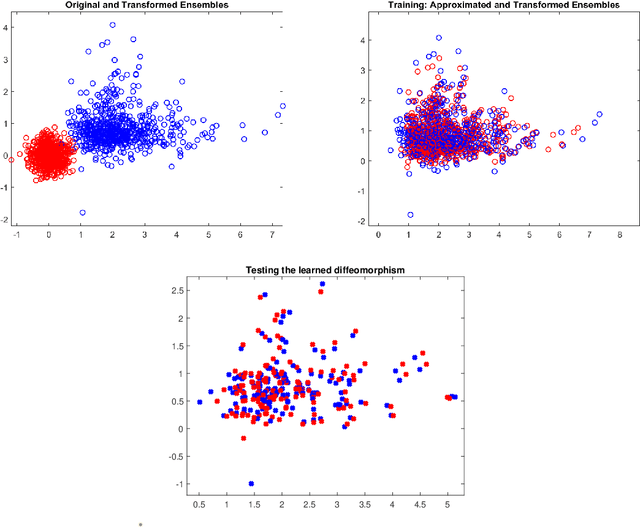
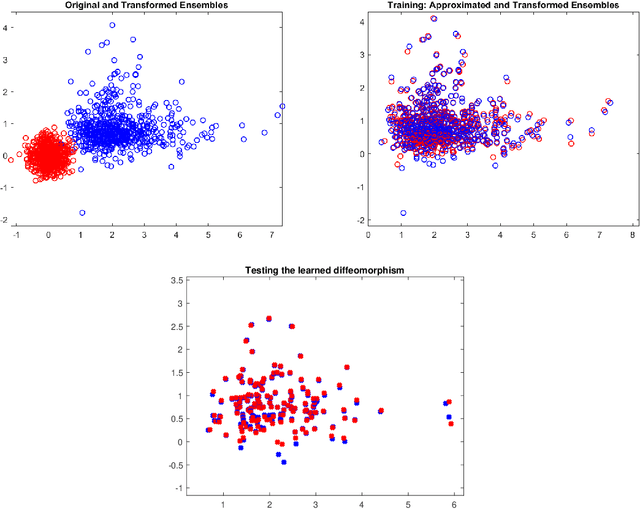
In this paper we propose a Deep Learning architecture to approximate diffeomorphisms isotopic to the identity. We consider a control system of the form $\dot x = \sum_{i=1}^lF_i(x)u_i$, with linear dependence in the controls, and we use the corresponding flow to approximate the action of a diffeomorphism on a compact ensemble of points. Despite the simplicity of the control system, it has been recently shown that a Universal Approximation Property holds. The problem of minimizing the sum of the training error and of a regularizing term induces a gradient flow in the space of admissible controls. A possible training procedure for the discrete-time neural network consists in projecting the gradient flow onto a finite-dimensional subspace of the admissible controls. An alternative approach relies on an iterative method based on Pontryagin Maximum Principle for the numerical resolution of Optimal Control problems. Here the maximization of the Hamiltonian can be carried out with an extremely low computational effort, owing to the linear dependence of the system in the control variables.