Approximation Theory, Computing, and Deep Learning on the Wasserstein Space

The challenge of approximating functions in infinite-dimensional spaces from finite samples is widely regarded as formidable. In this study, we delve into the challenging problem of the numerical approximation of Sobolev-smooth functions defined on probability spaces. Our particular focus centers on the Wasserstein distance function, which serves as a relevant example. In contrast to the existing body of literature focused on approximating efficiently pointwise evaluations, we chart a new course to define functional approximants by adopting three machine learning-based approaches: 1. Solving a finite number of optimal transport problems and computing the corresponding Wasserstein potentials. 2. Employing empirical risk minimization with Tikhonov regularization in Wasserstein Sobolev spaces. 3. Addressing the problem through the saddle point formulation that characterizes the weak form of the Tikhonov functional's Euler-Lagrange equation. As a theoretical contribution, we furnish explicit and quantitative bounds on generalization errors for each of these solutions. In the proofs, we leverage the theory of metric Sobolev spaces and we combine it with techniques of optimal transport, variational calculus, and large deviation bounds. In our numerical implementation, we harness appropriately designed neural networks to serve as basis functions. These networks undergo training using diverse methodologies. This approach allows us to obtain approximating functions that can be rapidly evaluated after training. Consequently, our constructive solutions significantly enhance at equal accuracy the evaluation speed, surpassing that of state-of-the-art methods by several orders of magnitude.

From NeurODEs to AutoencODEs: a mean-field control framework for width-varying Neural Networks

In our work, we build upon the established connection between Residual Neural Networks (ResNets) and continuous-time control systems known as NeurODEs. By construction, NeurODEs have been limited to constant-width layers, making them unsuitable for modeling deep learning architectures with width-varying layers. In this paper, we propose a continuous-time Autoencoder, which we call AutoencODE, and we extend to this case the mean-field control framework already developed for usual NeurODEs. In this setting, we tackle the case of low Tikhonov regularization, resulting in potentially non-convex cost landscapes. While the global results obtained for high Tikhonov regularization may not hold globally, we show that many of them can be recovered in regions where the loss function is locally convex. Inspired by our theoretical findings, we develop a training method tailored to this specific type of Autoencoders with residual connections, and we validate our approach through numerical experiments conducted on various examples.

Gradient is All You Need?

In this paper we provide a novel analytical perspective on the theoretical understanding of gradient-based learning algorithms by interpreting consensus-based optimization (CBO), a recently proposed multi-particle derivative-free optimization method, as a stochastic relaxation of gradient descent. Remarkably, we observe that through communication of the particles, CBO exhibits a stochastic gradient descent (SGD)-like behavior despite solely relying on evaluations of the objective function. The fundamental value of such link between CBO and SGD lies in the fact that CBO is provably globally convergent to global minimizers for ample classes of nonsmooth and nonconvex objective functions, hence, on the one side, offering a novel explanation for the success of stochastic relaxations of gradient descent. On the other side, contrary to the conventional wisdom for which zero-order methods ought to be inefficient or not to possess generalization abilities, our results unveil an intrinsic gradient descent nature of such heuristics. This viewpoint furthermore complements previous insights into the working principles of CBO, which describe the dynamics in the mean-field limit through a nonlinear nonlocal partial differential equation that allows to alleviate complexities of the nonconvex function landscape. Our proofs leverage a completely nonsmooth analysis, which combines a novel quantitative version of the Laplace principle (log-sum-exp trick) and the minimizing movement scheme (proximal iteration). In doing so, we furnish useful and precise insights that explain how stochastic perturbations of gradient descent overcome energy barriers and reach deep levels of nonconvex functions. Instructive numerical illustrations support the provided theoretical insights.

Finite Sample Identification of Wide Shallow Neural Networks with Biases

Artificial neural networks are functions depending on a finite number of parameters typically encoded as weights and biases. The identification of the parameters of the network from finite samples of input-output pairs is often referred to as the \emph{teacher-student model}, and this model has represented a popular framework for understanding training and generalization. Even if the problem is NP-complete in the worst case, a rapidly growing literature -- after adding suitable distributional assumptions -- has established finite sample identification of two-layer networks with a number of neurons $m=\mathcal O(D)$, $D$ being the input dimension. For the range $D<m<D^2$ the problem becomes harder, and truly little is known for networks parametrized by biases as well. This paper fills the gap by providing constructive methods and theoretical guarantees of finite sample identification for such wider shallow networks with biases. Our approach is based on a two-step pipeline: first, we recover the direction of the weights, by exploiting second order information; next, we identify the signs by suitable algebraic evaluations, and we recover the biases by empirical risk minimization via gradient descent. Numerical results demonstrate the effectiveness of our approach.

Stable Recovery of Entangled Weights: Towards Robust Identification of Deep Neural Networks from Minimal Samples

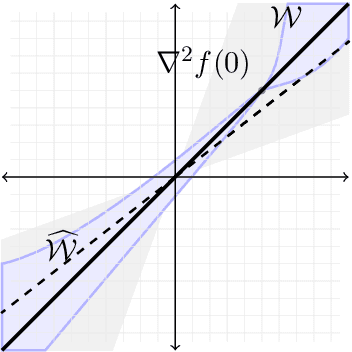
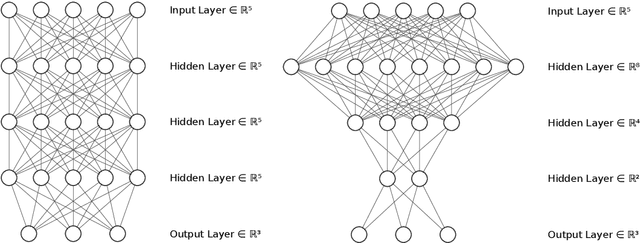
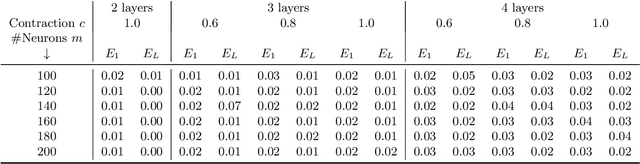
In this paper we approach the problem of unique and stable identifiability of generic deep artificial neural networks with pyramidal shape and smooth activation functions from a finite number of input-output samples. More specifically we introduce the so-called entangled weights, which compose weights of successive layers intertwined with suitable diagonal and invertible matrices depending on the activation functions and their shifts. We prove that entangled weights are completely and stably approximated by an efficient and robust algorithm as soon as $\mathcal O(D^2 \times m)$ nonadaptive input-output samples of the network are collected, where $D$ is the input dimension and $m$ is the number of neurons of the network. Moreover, we empirically observe that the approach applies to networks with up to $\mathcal O(D \times m_L)$ neurons, where $m_L$ is the number of output neurons at layer $L$. Provided knowledge of layer assignments of entangled weights and of remaining scaling and shift parameters, which may be further heuristically obtained by least squares, the entangled weights identify the network completely and uniquely. To highlight the relevance of the theoretical result of stable recovery of entangled weights, we present numerical experiments, which demonstrate that multilayered networks with generic weights can be robustly identified and therefore uniformly approximated by the presented algorithmic pipeline. In contrast backpropagation cannot generalize stably very well in this setting, being always limited by relatively large uniform error. In terms of practical impact, our study shows that we can relate input-output information uniquely and stably to network parameters, providing a form of explainability. Moreover, our method paves the way for compression of overparametrized networks and for the training of minimal complexity networks.

Consensus-based Optimization on the Sphere II: Convergence to Global Minimizers and Machine Learning

We present the implementation of a new stochastic Kuramoto-Vicsek-type model for global optimization of nonconvex functions on the sphere. This model belongs to the class of Consensus-Based Optimization. In fact, particles move on the sphere driven by a drift towards an instantaneous consensus point, which is computed as a convex combination of particle locations, weighted by the cost function according to Laplace's principle, and it represents an approximation to a global minimizer. The dynamics is further perturbed by a random vector field to favor exploration, whose variance is a function of the distance of the particles to the consensus point. In particular, as soon as the consensus is reached the stochastic component vanishes. The main results of this paper are about the proof of convergence of the numerical scheme to global minimizers provided conditions of well-preparation of the initial datum. The proof combines previous results of mean-field limit with a novel asymptotic analysis, and classical convergence results of numerical methods for SDE. We present several numerical experiments, which show that the algorithm proposed in the present paper scales well with the dimension and is extremely versatile. To quantify the performances of the new approach, we show that the algorithm is able to perform essentially as good as ad hoc state of the art methods in challenging problems in signal processing and machine learning, namely the phase retrieval problem and the robust subspace detection.

Consensus-Based Optimization on the Sphere I: Well-Posedness and Mean-Field Limit

We introduce a new stochastic Kuramoto-Vicsek-type model for global optimization of nonconvex functions on the sphere. This model belongs to the class of Consensus-Based Optimization methods. In fact, particles move on the sphere driven by a drift towards an instantaneous consensus point, computed as a convex combination of the particle locations weighted by the cost function according to Laplace's principle. The consensus point represents an approximation to a global minimizer. The dynamics is further perturbed by a random vector field to favor exploration, whose variance is a function of the distance of the particles to the consensus point. In particular, as soon as the consensus is reached, then the stochastic component vanishes. In this paper, we study the well-posedness of the model and we derive rigorously its mean-field approximation for large particle limit.

Data-driven Evolutions of Critical Points

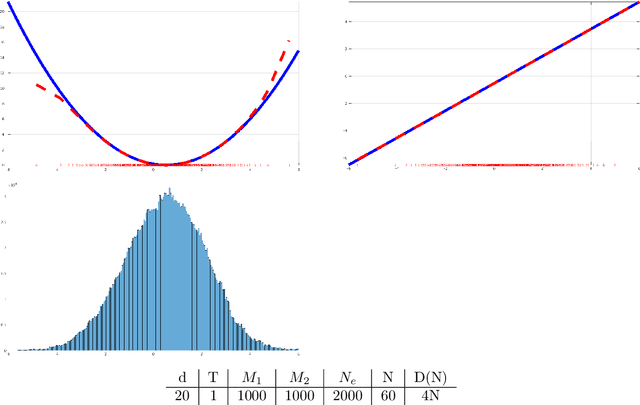
In this paper we are concerned with the learnability of energies from data obtained by observing time evolutions of their critical points starting at random initial equilibria. As a byproduct of our theoretical framework we introduce the novel concept of mean-field limit of critical point evolutions and of their energy balance as a new form of transport. We formulate the energy learning as a variational problem, minimizing the discrepancy of energy competitors from fulfilling the equilibrium condition along any trajectory of critical points originated at random initial equilibria. By Gamma-convergence arguments we prove the convergence of minimal solutions obtained from finite number of observations to the exact energy in a suitable sense. The abstract framework is actually fully constructive and numerically implementable. Hence, the approximation of the energy from a finite number of observations of past evolutions allows to simulate further evolutions, which are fully data-driven. As we aim at a precise quantitative analysis, and to provide concrete examples of tractable solutions, we present analytic and numerical results on the reconstruction of an elastic energy for a one-dimensional model of thin nonlinear-elastic rod.

Robust and Resource Efficient Identification of Two Hidden Layer Neural Networks

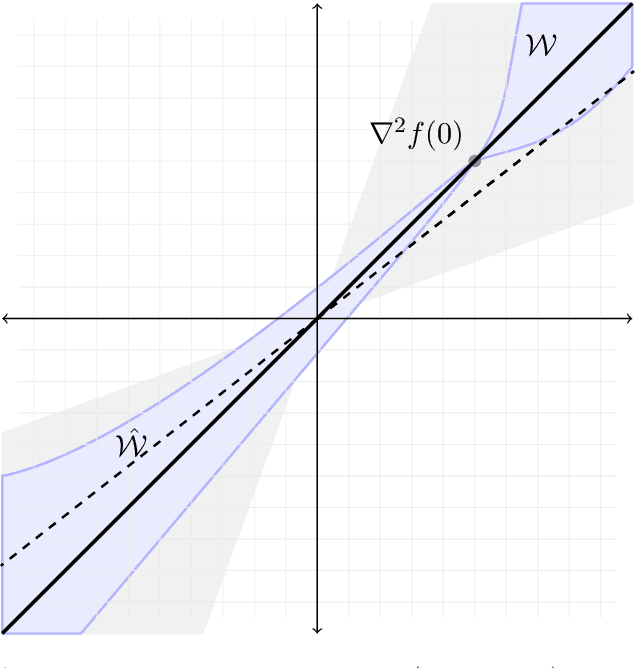
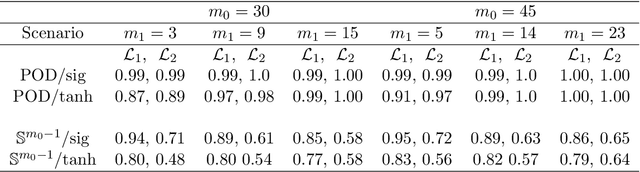
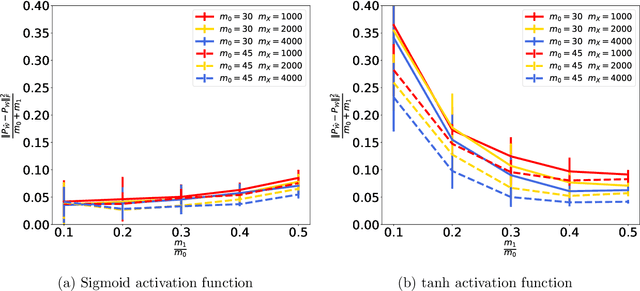
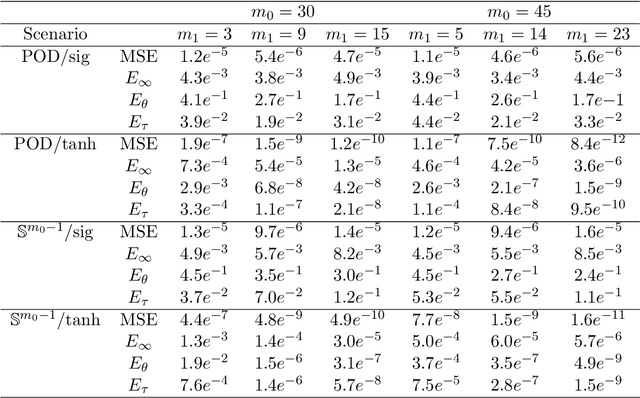
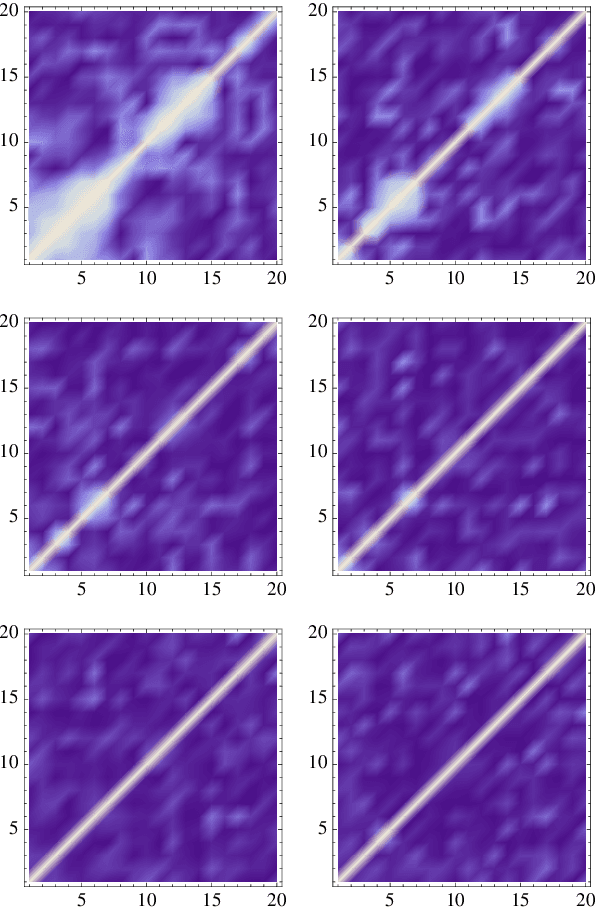
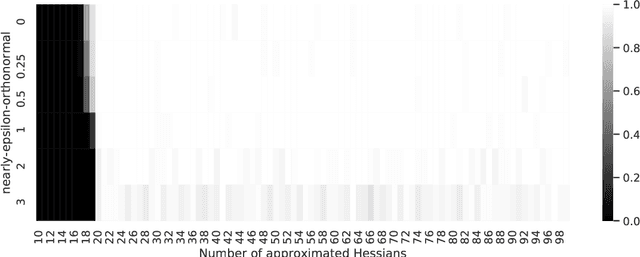
We address the structure identification and the uniform approximation of two fully nonlinear layer neural networks of the type $f(x)=1^T h(B^T g(A^T x))$ on $\mathbb R^d$ from a small number of query samples. We approach the problem by sampling actively finite difference approximations to Hessians of the network. Gathering several approximate Hessians allows reliably to approximate the matrix subspace $\mathcal W$ spanned by symmetric tensors $a_1 \otimes a_1 ,\dots,a_{m_0}\otimes a_{m_0}$ formed by weights of the first layer together with the entangled symmetric tensors $v_1 \otimes v_1 ,\dots,v_{m_1}\otimes v_{m_1}$, formed by suitable combinations of the weights of the first and second layer as $v_\ell=A G_0 b_\ell/\|A G_0 b_\ell\|_2$, $\ell \in [m_1]$, for a diagonal matrix $G_0$ depending on the activation functions of the first layer. The identification of the 1-rank symmetric tensors within $\mathcal W$ is then performed by the solution of a robust nonlinear program. We provide guarantees of stable recovery under a posteriori verifiable conditions. We further address the correct attribution of approximate weights to the first or second layer. By using a suitably adapted gradient descent iteration, it is possible then to estimate, up to intrinsic symmetries, the shifts of the activations functions of the first layer and compute exactly the matrix $G_0$. Our method of identification of the weights of the network is fully constructive, with quantifiable sample complexity, and therefore contributes to dwindle the black-box nature of the network training phase. We corroborate our theoretical results by extensive numerical experiments.

Identification of Shallow Neural Networks by Fewest Samples

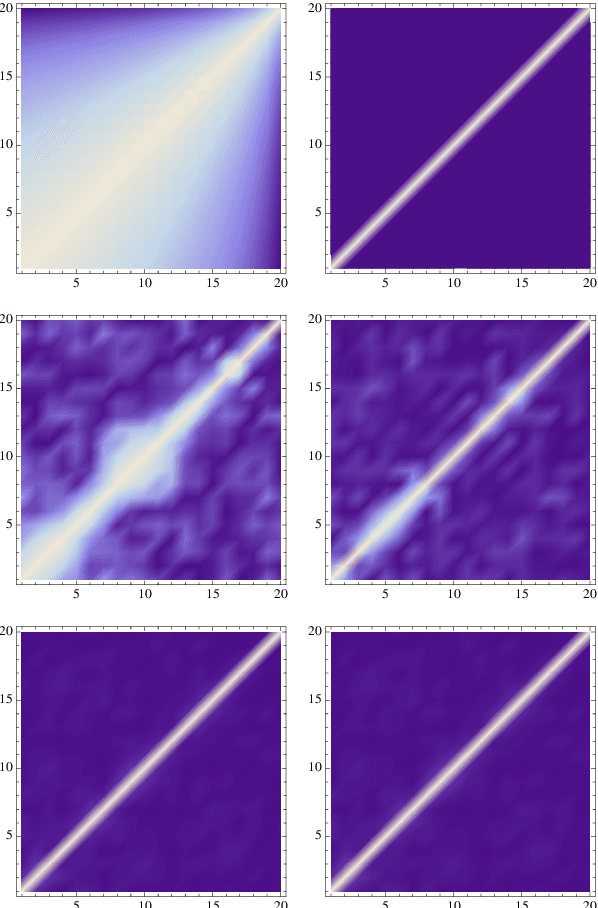
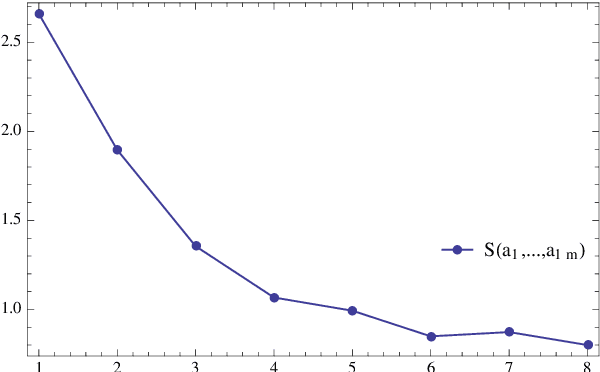
We address the uniform approximation of sums of ridge functions $\sum_{i=1}^m g_i(a_i\cdot x)$ on ${\mathbb R}^d$, representing the shallowest form of feed-forward neural network, from a small number of query samples, under mild smoothness assumptions on the functions $g_i$'s and near-orthogonality of the ridge directions $a_i$'s. The sample points are randomly generated and are universal, in the sense that the sampled queries on those points will allow the proposed recovery algorithms to perform a uniform approximation of any sum of ridge functions with high-probability. Our general approximation strategy is developed as a sequence of algorithms to perform individual sub-tasks. We first approximate the span of the ridge directions. Then we use a straightforward substitution, which reduces the dimensionality of the problem from $d$ to $m$. The core of the construction is then the approximation of ridge directions expressed in terms of rank-$1$ matrices $a_i \otimes a_i$, realized by formulating their individual identification as a suitable nonlinear program, maximizing the spectral norm of certain competitors constrained over the unit Frobenius sphere. The final step is then to approximate the functions $g_1,\dots,g_m$ by $\hat g_1,\dots,\hat g_m$. Higher order differentiation, as used in our construction, of sums of ridge functions or of their compositions, as in deeper neural network, yields a natural connection between neural network weight identification and tensor product decomposition identification. In the case of the shallowest feed-forward neural network, we show that second order differentiation and tensors of order two (i.e., matrices) suffice.