Statistical Learning Theory for Distributional Classification

In supervised learning with distributional inputs in the two-stage sampling setup, relevant to applications like learning-based medical screening or causal learning, the inputs (which are probability distributions) are not accessible in the learning phase, but only samples thereof. This problem is particularly amenable to kernel-based learning methods, where the distributions or samples are first embedded into a Hilbert space, often using kernel mean embeddings (KMEs), and then a standard kernel method like Support Vector Machines (SVMs) is applied, using a kernel defined on the embedding Hilbert space. In this work, we contribute to the theoretical analysis of this latter approach, with a particular focus on classification with distributional inputs using SVMs. We establish a new oracle inequality and derive consistency and learning rate results. Furthermore, for SVMs using the hinge loss and Gaussian kernels, we formulate a novel variant of an established noise assumption from the binary classification literature, under which we can establish learning rates. Finally, some of our technical tools like a new feature space for Gaussian kernels on Hilbert spaces are of independent interest.

A kernel conditional two-sample test

We propose a framework for hypothesis testing on conditional probability distributions, which we then use to construct conditional two-sample statistical tests. These tests identify the inputs -- called covariates in this context -- where two conditional expectations differ with high probability. Our key idea is to transform confidence bounds of a learning method into a conditional two-sample test, and we instantiate this principle for kernel ridge regression (KRR) and conditional kernel mean embeddings. We generalize existing pointwise-in-time or time-uniform confidence bounds for KRR to previously-inaccessible yet essential cases such as infinite-dimensional outputs with non-trace-class kernels. These bounds enable circumventing the need for independent data in our statistical tests, since they allow online sampling. We also introduce bootstrapping schemes leveraging the parametric form of testing thresholds identified in theory to avoid tuning inaccessible parameters, making our method readily applicable in practice. Such conditional two-sample tests are especially relevant in applications where data arrive sequentially or non-independently, or when output distributions vary with operational parameters. We demonstrate their utility through examples in process monitoring and comparison of dynamical systems. Overall, our results establish a comprehensive foundation for conditional two-sample testing, from theoretical guarantees to practical implementation, and advance the state-of-the-art on the concentration of vector-valued least squares estimation.

Safety in safe Bayesian optimization and its ramifications for control

A recurring and important task in control engineering is parameter tuning under constraints, which conceptually amounts to optimization of a blackbox function accessible only through noisy evaluations. For example, in control practice parameters of a pre-designed controller are often tuned online in feedback with a plant, and only safe parameter values should be tried, avoiding for example instability. Recently, machine learning methods have been deployed for this important problem, in particular, Bayesian optimization (BO). To handle safety constraints, algorithms from safe BO have been utilized, especially SafeOpt-type algorithms, which enjoy considerable popularity in learning-based control, robotics, and adjacent fields. However, we identify two significant obstacles to practical safety. First, SafeOpt-type algorithms rely on quantitative uncertainty bounds, and most implementations replace these by theoretically unsupported heuristics. Second, the theoretically valid uncertainty bounds crucially depend on a quantity - the reproducing kernel Hilbert space norm of the target function - that at present is impossible to reliably bound using established prior engineering knowledge. By careful numerical experiments we show that these issues can indeed cause safety violations. To overcome these problems, we propose Lipschitz-only Safe Bayesian Optimization (LoSBO), a safe BO algorithm that relies only on a known Lipschitz bound for its safety. Furthermore, we propose a variant (LoS-GP-UCB) that avoids gridding of the search space and is therefore applicable even for moderately high-dimensional problems.

On Safety in Safe Bayesian Optimization

Optimizing an unknown function under safety constraints is a central task in robotics, biomedical engineering, and many other disciplines, and increasingly safe Bayesian Optimization (BO) is used for this. Due to the safety critical nature of these applications, it is of utmost importance that theoretical safety guarantees for these algorithms translate into the real world. In this work, we investigate three safety-related issues of the popular class of SafeOpt-type algorithms. First, these algorithms critically rely on frequentist uncertainty bounds for Gaussian Process (GP) regression, but concrete implementations typically utilize heuristics that invalidate all safety guarantees. We provide a detailed analysis of this problem and introduce Real-\b{eta}-SafeOpt, a variant of the SafeOpt algorithm that leverages recent GP bounds and thus retains all theoretical guarantees. Second, we identify assuming an upper bound on the reproducing kernel Hilbert space (RKHS) norm of the target function, a key technical assumption in SafeOpt-like algorithms, as a central obstacle to real-world usage. To overcome this challenge, we introduce the Lipschitz-only Safe Bayesian Optimization (LoSBO) algorithm, which guarantees safety without an assumption on the RKHS bound, and empirically show that this algorithm is not only safe, but also exhibits superior performance compared to the state-of-the-art on several function classes. Third, SafeOpt and derived algorithms rely on a discrete search space, making them difficult to apply to higher-dimensional problems. To widen the applicability of these algorithms, we introduce Lipschitz-only GP-UCB (LoS-GP-UCB), a variant of LoSBO applicable to moderately high-dimensional problems, while retaining safety.

Automatic nonlinear MPC approximation with closed-loop guarantees

In this paper, we address the problem of automatically approximating nonlinear model predictive control (MPC) schemes with closed-loop guarantees. First, we discuss how this problem can be reduced to a function approximation problem, which we then tackle by proposing ALKIA-X, the Adaptive and Localized Kernel Interpolation Algorithm with eXtrapolated reproducing kernel Hilbert space norm. ALKIA-X is a non-iterative algorithm that ensures numerically well-conditioned computations, a fast-to-evaluate approximating function, and the guaranteed satisfaction of any desired bound on the approximation error. Hence, ALKIA-X automatically computes an explicit function that approximates the MPC, yielding a controller suitable for safety-critical systems and high sampling rates. In a numerical experiment, we apply ALKIA-X to a nonlinear MPC scheme, demonstrating reduced offline computation and online evaluation time compared to a state-of-the-art method.

Lipschitz and Hölder Continuity in Reproducing Kernel Hilbert Spaces

Reproducing kernel Hilbert spaces (RKHSs) are very important function spaces, playing an important role in machine learning, statistics, numerical analysis and pure mathematics. Since Lipschitz and H\"older continuity are important regularity properties, with many applications in interpolation, approximation and optimization problems, in this work we investigate these continuity notion in RKHSs. We provide several sufficient conditions as well as an in depth investigation of reproducing kernels inducing prescribed Lipschitz or H\"older continuity. Apart from new results, we also collect related known results from the literature, making the present work also a convenient reference on this topic.

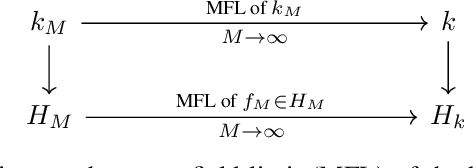
On kernel-based statistical learning in the mean field limit

In many applications of machine learning, a large number of variables are considered. Motivated by machine learning of interacting particle systems, we consider the situation when the number of input variables goes to infinity. First, we continue the recent investigation of the mean field limit of kernels and their reproducing kernel Hilbert spaces, completing the existing theory. Next, we provide results relevant for approximation with such kernels in the mean field limit, including a representer theorem. Finally, we use these kernels in the context of statistical learning in the mean field limit, focusing on Support Vector Machines. In particular, we show mean field convergence of empirical and infinite-sample solutions as well as the convergence of the corresponding risks. On the one hand, our results establish rigorous mean field limits in the context of kernel methods, providing new theoretical tools and insights for large-scale problems. On the other hand, our setting corresponds to a new form of limit of learning problems, which seems to have not been investigated yet in the statistical learning theory literature.

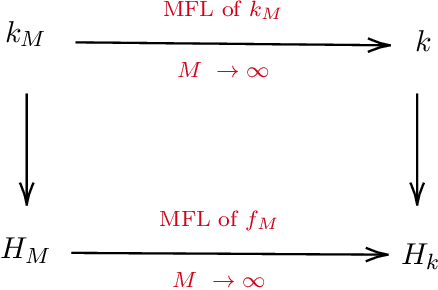
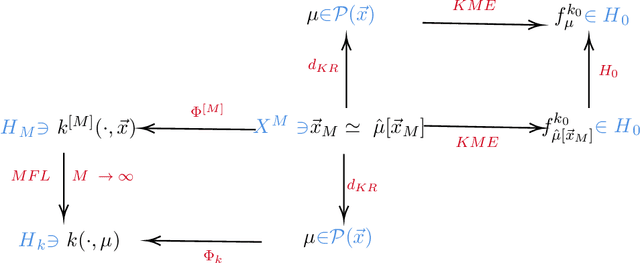
Reproducing kernel Hilbert spaces in the mean field limit

Kernel methods, being supported by a well-developed theory and coming with efficient algorithms, are among the most popular and successful machine learning techniques. From a mathematical point of view, these methods rest on the concept of kernels and function spaces generated by kernels, so called reproducing kernel Hilbert spaces. Motivated by recent developments of learning approaches in the context of interacting particle systems, we investigate kernel methods acting on data with many measurement variables. We show the rigorous mean field limit of kernels and provide a detailed analysis of the limiting reproducing kernel Hilbert space. Furthermore, several examples of kernels, that allow a rigorous mean field limit, are presented.

Learning-enhanced robust controller synthesis with rigorous statistical and control-theoretic guarantees

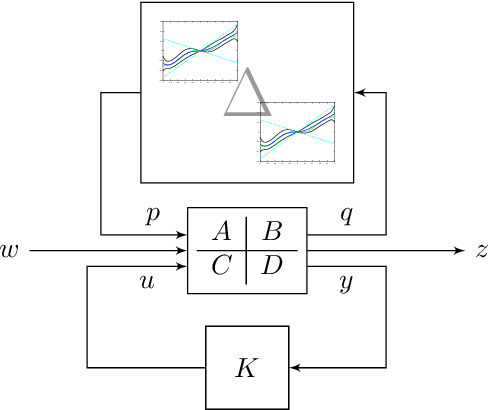
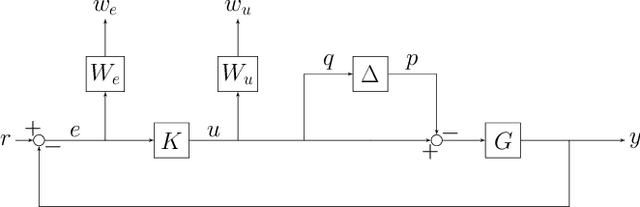
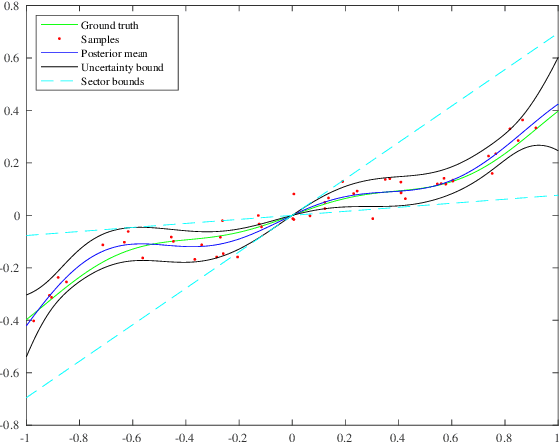
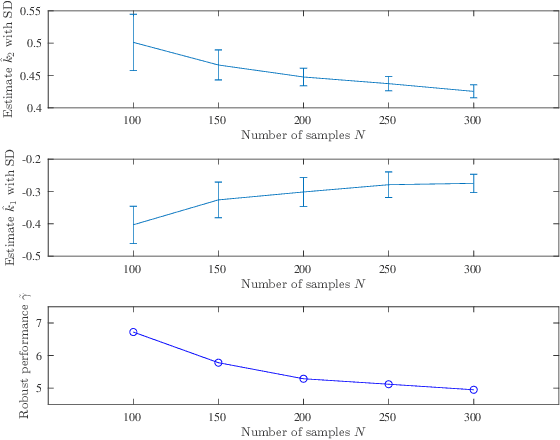
The combination of machine learning with control offers many opportunities, in particular for robust control. However, due to strong safety and reliability requirements in many real-world applications, providing rigorous statistical and control-theoretic guarantees is of utmost importance, yet difficult to achieve for learning-based control schemes. We present a general framework for learning-enhanced robust control that allows for systematic integration of prior engineering knowledge, is fully compatible with modern robust control and still comes with rigorous and practically meaningful guarantees. Building on the established Linear Fractional Representation and Integral Quadratic Constraints framework, we integrate Gaussian Process Regression as a learning component and state-of-the-art robust controller synthesis. In a concrete robust control example, our approach is demonstrated to yield improved performance with more data, while guarantees are maintained throughout.

Practical and Rigorous Uncertainty Bounds for Gaussian Process Regression

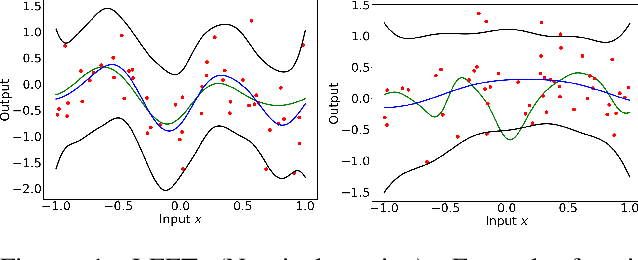
Gaussian Process Regression is a popular nonparametric regression method based on Bayesian principles that provides uncertainty estimates for its predictions. However, these estimates are of a Bayesian nature, whereas for some important applications, like learning-based control with safety guarantees, frequentist uncertainty bounds are required. Although such rigorous bounds are available for Gaussian Processes, they are too conservative to be useful in applications. This often leads practitioners to replacing these bounds by heuristics, thus breaking all theoretical guarantees. To address this problem, we introduce new uncertainty bounds that are rigorous, yet practically useful at the same time. In particular, the bounds can be explicitly evaluated and are much less conservative than state of the art results. Furthermore, we show that certain model misspecifications lead to only graceful degradation. We demonstrate these advantages and the usefulness of our results for learning-based control with numerical examples.