Johannes Köhler
An MPC framework for efficient navigation of mobile robots in cluttered environments
Sep 19, 2025Abstract:We present a model predictive control (MPC) framework for efficient navigation of mobile robots in cluttered environments. The proposed approach integrates a finite-segment shortest path planner into the finite-horizon trajectory optimization of the MPC. This formulation ensures convergence to dynamically selected targets and guarantees collision avoidance, even under general nonlinear dynamics and cluttered environments. The approach is validated through hardware experiments on a small ground robot, where a human operator dynamically assigns target locations. The robot successfully navigated through complex environments and reached new targets within 2-3 seconds.
Model Predictive Control with Reference Learning for Soft Robotic Intracranial Pressure Waveform Modulation
Sep 16, 2025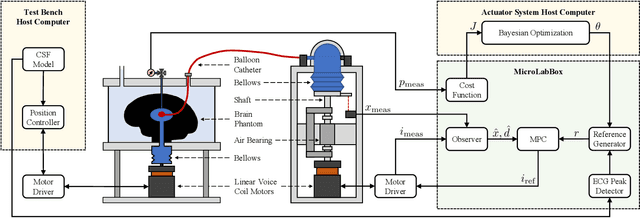
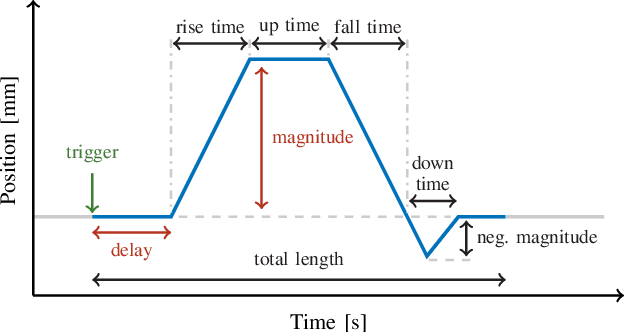
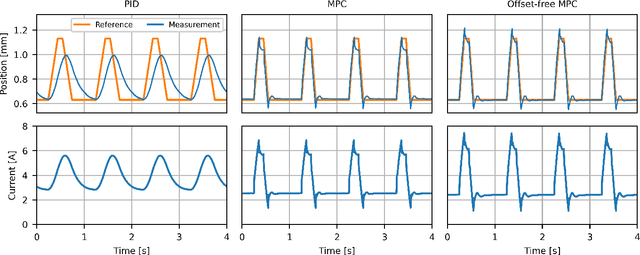
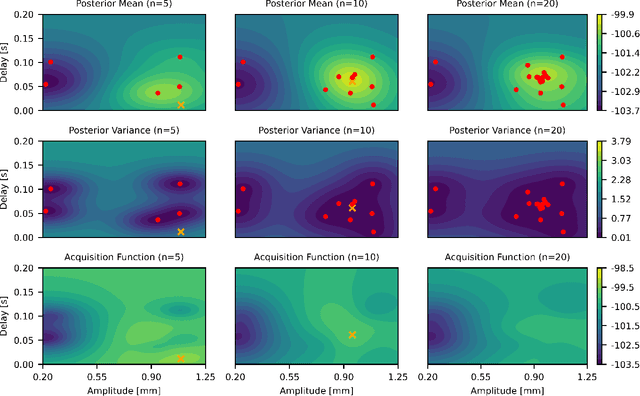
Abstract:This paper introduces a learning-based control framework for a soft robotic actuator system designed to modulate intracranial pressure (ICP) waveforms, which is essential for studying cerebrospinal fluid dynamics and pathological processes underlying neurological disorders. A two-layer framework is proposed to safely achieve a desired ICP waveform modulation. First, a model predictive controller (MPC) with a disturbance observer is used for offset-free tracking of the system's motor position reference trajectory under safety constraints. Second, to address the unknown nonlinear dependence of ICP on the motor position, we employ a Bayesian optimization (BO) algorithm used for online learning of a motor position reference trajectory that yields the desired ICP modulation. The framework is experimentally validated using a test bench with a brain phantom that replicates realistic ICP dynamics in vitro. Compared to a previously employed proportional-integral-derivative controller, the MPC reduces mean and maximum motor position reference tracking errors by 83 % and 73 %, respectively. In less than 20 iterations, the BO algorithm learns a motor position reference trajectory that yields an ICP waveform with the desired mean and amplitude.
Robust Convex Model Predictive Control with collision avoidance guarantees for robot manipulators
Aug 29, 2025Abstract:Industrial manipulators are normally operated in cluttered environments, making safe motion planning important. Furthermore, the presence of model-uncertainties make safe motion planning more difficult. Therefore, in practice the speed is limited in order to reduce the effect of disturbances. There is a need for control methods that can guarantee safe motions that can be executed fast. We address this need by suggesting a novel model predictive control (MPC) solution for manipulators, where our two main components are a robust tube MPC and a corridor planning algorithm to obtain collision-free motion. Our solution results in a convex MPC, which we can solve fast, making our method practically useful. We demonstrate the efficacy of our method in a simulated environment with a 6 DOF industrial robot operating in cluttered environments with uncertainties in model parameters. We outperform benchmark methods, both in terms of being able to work under higher levels of model uncertainties, while also yielding faster motion.
From Data to Safe Mobile Robot Navigation: An Efficient and Modular Robust MPC Design Pipeline
Aug 09, 2025Abstract:Model predictive control (MPC) is a powerful strategy for planning and control in autonomous mobile robot navigation. However, ensuring safety in real-world deployments remains challenging due to the presence of disturbances and measurement noise. Existing approaches often rely on idealized assumptions, neglect the impact of noisy measurements, and simply heuristically guess unrealistic bounds. In this work, we present an efficient and modular robust MPC design pipeline that systematically addresses these limitations. The pipeline consists of an iterative procedure that leverages closed-loop experimental data to estimate disturbance bounds and synthesize a robust output-feedback MPC scheme. We provide the pipeline in the form of deterministic and reproducible code to synthesize the robust output-feedback MPC from data. We empirically demonstrate robust constraint satisfaction and recursive feasibility in quadrotor simulations using Gazebo.
A Step-by-step Guide on Nonlinear Model Predictive Control for Safe Mobile Robot Navigation
Jul 23, 2025Abstract:Designing a Model Predictive Control (MPC) scheme that enables a mobile robot to safely navigate through an obstacle-filled environment is a complicated yet essential task in robotics. In this technical report, safety refers to ensuring that the robot respects state and input constraints while avoiding collisions with obstacles despite the presence of disturbances and measurement noise. This report offers a step-by-step approach to implementing Nonlinear Model Predictive Control (NMPC) schemes addressing these safety requirements. Numerous books and survey papers provide comprehensive overviews of linear MPC (LMPC) \cite{bemporad2007robust,kouvaritakis2016model}, NMPC \cite{rawlings2017model,allgower2004nonlinear,mayne2014model,grune2017nonlinear,saltik2018outlook}, and their applications in various domains, including robotics \cite{nascimento2018nonholonomic,nguyen2021model,shi2021advanced,wei2022mpc}. This report does not aim to replicate those exhaustive reviews. Instead, it focuses specifically on NMPC as a foundation for safe mobile robot navigation. The goal is to provide a practical and accessible path from theoretical concepts to mathematical proofs and implementation, emphasizing safety and performance guarantees. It is intended for researchers, robotics engineers, and practitioners seeking to bridge the gap between theoretical NMPC formulations and real-world robotic applications. This report is not necessarily meant to remain fixed over time. If someone finds an error in the presented theory, please reach out via the given email addresses. We are happy to update the document if necessary.
A robust and adaptive MPC formulation for Gaussian process models
Jul 02, 2025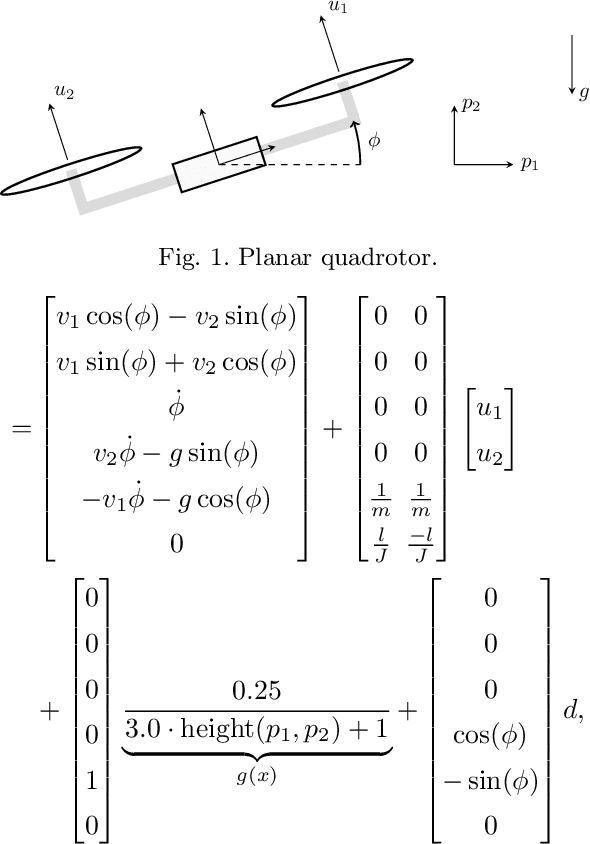

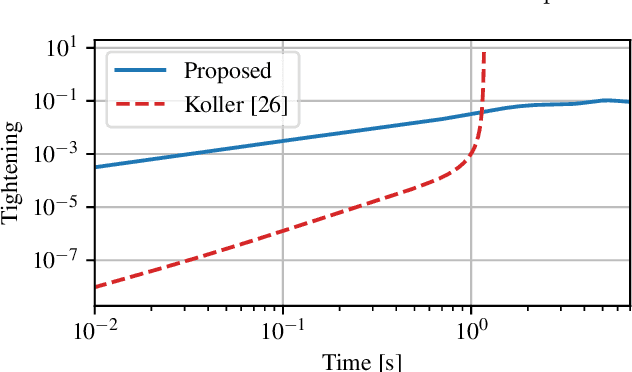
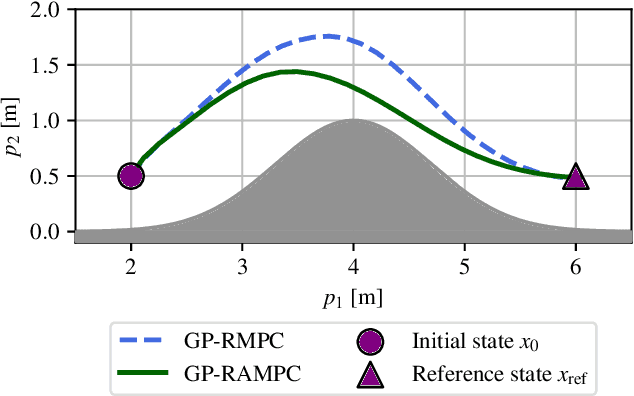
Abstract:In this paper, we present a robust and adaptive model predictive control (MPC) framework for uncertain nonlinear systems affected by bounded disturbances and unmodeled nonlinearities. We use Gaussian Processes (GPs) to learn the uncertain dynamics based on noisy measurements, including those collected during system operation. As a key contribution, we derive robust predictions for GP models using contraction metrics, which are incorporated in the MPC formulation. The proposed design guarantees recursive feasibility, robust constraint satisfaction and convergence to a reference state, with high probability. We provide a numerical example of a planar quadrotor subject to difficult-to-model ground effects, which highlights significant improvements achieved through the proposed robust prediction method and through online learning.
Time-Varying Coverage Control: A Distributed Tracker-Planner MPC Framework
Jul 02, 2025Abstract:Time-varying coverage control addresses the challenge of coordinating multiple agents covering an environment where regions of interest change over time. This problem has broad applications, including the deployment of autonomous taxis and coordination in search and rescue operations. The achievement of effective coverage is complicated by the presence of time-varying density functions, nonlinear agent dynamics, and stringent system and safety constraints. In this paper, we present a distributed multi-agent control framework for time-varying coverage under nonlinear constrained dynamics. Our approach integrates a reference trajectory planner and a tracking model predictive control (MPC) scheme, which operate at different frequencies within a multi-rate framework. For periodic density functions, we demonstrate closed-loop convergence to an optimal configuration of trajectories and provide formal guarantees regarding constraint satisfaction, collision avoidance, and recursive feasibility. Additionally, we propose an efficient algorithm capable of handling nonperiodic density functions, making the approach suitable for practical applications. Finally, we validate our method through hardware experiments using a fleet of four miniature race cars.
Optimal kernel regression bounds under energy-bounded noise
May 28, 2025Abstract:Non-conservative uncertainty bounds are key for both assessing an estimation algorithm's accuracy and in view of downstream tasks, such as its deployment in safety-critical contexts. In this paper, we derive a tight, non-asymptotic uncertainty bound for kernel-based estimation, which can also handle correlated noise sequences. Its computation relies on a mild norm-boundedness assumption on the unknown function and the noise, returning the worst-case function realization within the hypothesis class at an arbitrary query input location. The value of this function is shown to be given in terms of the posterior mean and covariance of a Gaussian process for an optimal choice of the measurement noise covariance. By rigorously analyzing the proposed approach and comparing it with other results in the literature, we show its effectiveness in returning tight and easy-to-compute bounds for kernel-based estimates.
Finite-Sample-Based Reachability for Safe Control with Gaussian Process Dynamics
May 12, 2025Abstract:Gaussian Process (GP) regression is shown to be effective for learning unknown dynamics, enabling efficient and safety-aware control strategies across diverse applications. However, existing GP-based model predictive control (GP-MPC) methods either rely on approximations, thus lacking guarantees, or are overly conservative, which limits their practical utility. To close this gap, we present a sampling-based framework that efficiently propagates the model's epistemic uncertainty while avoiding conservatism. We establish a novel sample complexity result that enables the construction of a reachable set using a finite number of dynamics functions sampled from the GP posterior. Building on this, we design a sampling-based GP-MPC scheme that is recursively feasible and guarantees closed-loop safety and stability with high probability. Finally, we showcase the effectiveness of our method on two numerical examples, highlighting accurate reachable set over-approximation and safe closed-loop performance.
Towards safe and tractable Gaussian process-based MPC: Efficient sampling within a sequential quadratic programming framework
Sep 13, 2024Abstract:Learning uncertain dynamics models using Gaussian process~(GP) regression has been demonstrated to enable high-performance and safety-aware control strategies for challenging real-world applications. Yet, for computational tractability, most approaches for Gaussian process-based model predictive control (GP-MPC) are based on approximations of the reachable set that are either overly conservative or impede the controller's safety guarantees. To address these challenges, we propose a robust GP-MPC formulation that guarantees constraint satisfaction with high probability. For its tractable implementation, we propose a sampling-based GP-MPC approach that iteratively generates consistent dynamics samples from the GP within a sequential quadratic programming framework. We highlight the improved reachable set approximation compared to existing methods, as well as real-time feasible computation times, using two numerical examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge