Finite Sample Identification of Wide Shallow Neural Networks with Biases

Artificial neural networks are functions depending on a finite number of parameters typically encoded as weights and biases. The identification of the parameters of the network from finite samples of input-output pairs is often referred to as the \emph{teacher-student model}, and this model has represented a popular framework for understanding training and generalization. Even if the problem is NP-complete in the worst case, a rapidly growing literature -- after adding suitable distributional assumptions -- has established finite sample identification of two-layer networks with a number of neurons $m=\mathcal O(D)$, $D$ being the input dimension. For the range $D<m<D^2$ the problem becomes harder, and truly little is known for networks parametrized by biases as well. This paper fills the gap by providing constructive methods and theoretical guarantees of finite sample identification for such wider shallow networks with biases. Our approach is based on a two-step pipeline: first, we recover the direction of the weights, by exploiting second order information; next, we identify the signs by suitable algebraic evaluations, and we recover the biases by empirical risk minimization via gradient descent. Numerical results demonstrate the effectiveness of our approach.

Stable Recovery of Entangled Weights: Towards Robust Identification of Deep Neural Networks from Minimal Samples

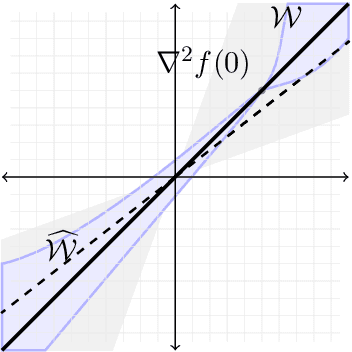
In this paper we approach the problem of unique and stable identifiability of generic deep artificial neural networks with pyramidal shape and smooth activation functions from a finite number of input-output samples. More specifically we introduce the so-called entangled weights, which compose weights of successive layers intertwined with suitable diagonal and invertible matrices depending on the activation functions and their shifts. We prove that entangled weights are completely and stably approximated by an efficient and robust algorithm as soon as $\mathcal O(D^2 \times m)$ nonadaptive input-output samples of the network are collected, where $D$ is the input dimension and $m$ is the number of neurons of the network. Moreover, we empirically observe that the approach applies to networks with up to $\mathcal O(D \times m_L)$ neurons, where $m_L$ is the number of output neurons at layer $L$. Provided knowledge of layer assignments of entangled weights and of remaining scaling and shift parameters, which may be further heuristically obtained by least squares, the entangled weights identify the network completely and uniquely. To highlight the relevance of the theoretical result of stable recovery of entangled weights, we present numerical experiments, which demonstrate that multilayered networks with generic weights can be robustly identified and therefore uniformly approximated by the presented algorithmic pipeline. In contrast backpropagation cannot generalize stably very well in this setting, being always limited by relatively large uniform error. In terms of practical impact, our study shows that we can relate input-output information uniquely and stably to network parameters, providing a form of explainability. Moreover, our method paves the way for compression of overparametrized networks and for the training of minimal complexity networks.

Robust and Resource Efficient Identification of Two Hidden Layer Neural Networks

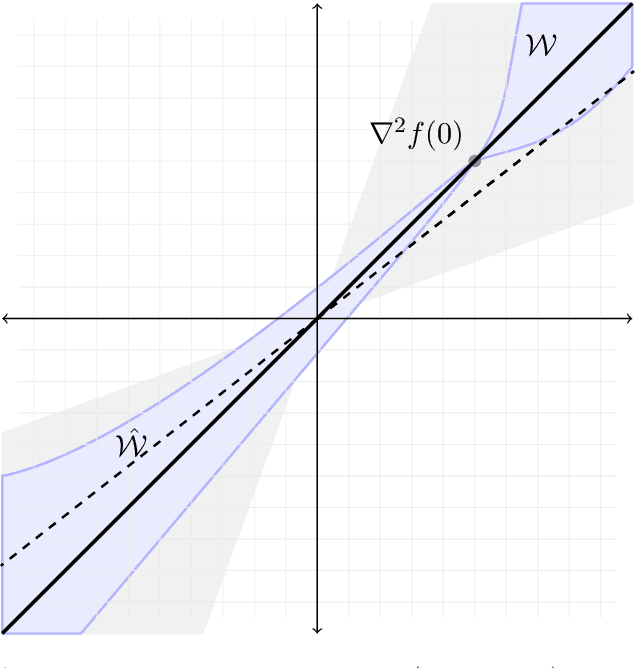
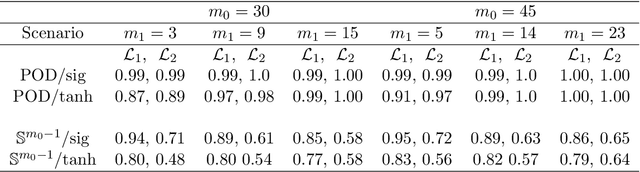
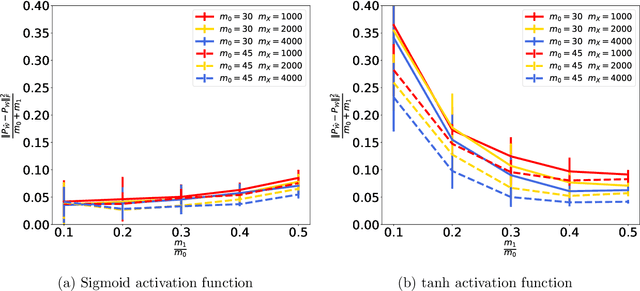
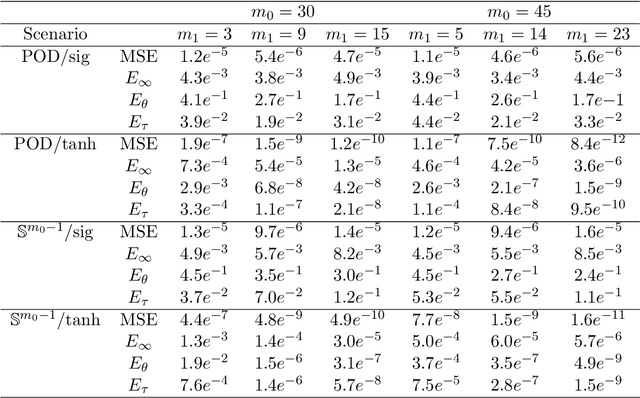
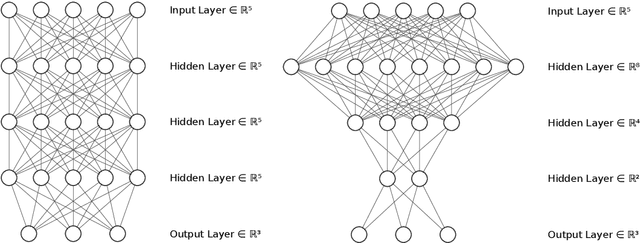
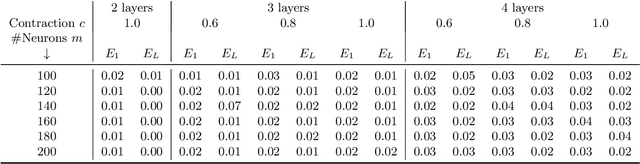
We address the structure identification and the uniform approximation of two fully nonlinear layer neural networks of the type $f(x)=1^T h(B^T g(A^T x))$ on $\mathbb R^d$ from a small number of query samples. We approach the problem by sampling actively finite difference approximations to Hessians of the network. Gathering several approximate Hessians allows reliably to approximate the matrix subspace $\mathcal W$ spanned by symmetric tensors $a_1 \otimes a_1 ,\dots,a_{m_0}\otimes a_{m_0}$ formed by weights of the first layer together with the entangled symmetric tensors $v_1 \otimes v_1 ,\dots,v_{m_1}\otimes v_{m_1}$, formed by suitable combinations of the weights of the first and second layer as $v_\ell=A G_0 b_\ell/\|A G_0 b_\ell\|_2$, $\ell \in [m_1]$, for a diagonal matrix $G_0$ depending on the activation functions of the first layer. The identification of the 1-rank symmetric tensors within $\mathcal W$ is then performed by the solution of a robust nonlinear program. We provide guarantees of stable recovery under a posteriori verifiable conditions. We further address the correct attribution of approximate weights to the first or second layer. By using a suitably adapted gradient descent iteration, it is possible then to estimate, up to intrinsic symmetries, the shifts of the activations functions of the first layer and compute exactly the matrix $G_0$. Our method of identification of the weights of the network is fully constructive, with quantifiable sample complexity, and therefore contributes to dwindle the black-box nature of the network training phase. We corroborate our theoretical results by extensive numerical experiments.