A Theory of How Pretraining Shapes Inductive Bias in Fine-Tuning

Pretraining and fine-tuning are central stages in modern machine learning systems. In practice, feature learning plays an important role across both stages: deep neural networks learn a broad range of useful features during pretraining and further refine those features during fine-tuning. However, an end-to-end theoretical understanding of how choices of initialization impact the ability to reuse and refine features during fine-tuning has remained elusive. Here we develop an analytical theory of the pretraining-fine-tuning pipeline in diagonal linear networks, deriving exact expressions for the generalization error as a function of initialization parameters and task statistics. We find that different initialization choices place the network into four distinct fine-tuning regimes that are distinguished by their ability to support feature learning and reuse, and therefore by the task statistics for which they are beneficial. In particular, a smaller initialization scale in earlier layers enables the network to both reuse and refine its features, leading to superior generalization on fine-tuning tasks that rely on a subset of pretraining features. We demonstrate empirically that the same initialization parameters impact generalization in nonlinear networks trained on CIFAR-100. Overall, our results demonstrate analytically how data and network initialization interact to shape fine-tuning generalization, highlighting an important role for the relative scale of initialization across different layers in enabling continued feature learning during fine-tuning.

Optimal Estimation in Orthogonally Invariant Generalized Linear Models: Spectral Initialization and Approximate Message Passing

We consider the problem of parameter estimation from a generalized linear model with a random design matrix that is orthogonally invariant in law. Such a model allows the design have an arbitrary distribution of singular values and only assumes that its singular vectors are generic. It is a vast generalization of the i.i.d. Gaussian design typically considered in the theoretical literature, and is motivated by the fact that real data often have a complex correlation structure so that methods relying on i.i.d. assumptions can be highly suboptimal. Building on the paradigm of spectrally-initialized iterative optimization, this paper proposes optimal spectral estimators and combines them with an approximate message passing (AMP) algorithm, establishing rigorous performance guarantees for these two algorithmic steps. Both the spectral initialization and the subsequent AMP meet existing conjectures on the fundamental limits to estimation -- the former on the optimal sample complexity for efficient weak recovery, and the latter on the optimal errors. Numerical experiments suggest the effectiveness of our methods and accuracy of our theory beyond orthogonally invariant data.

Full-Batch Gradient Descent Outperforms One-Pass SGD: Sample Complexity Separation in Single-Index Learning

It is folklore that reusing training data more than once can improve the statistical efficiency of gradient-based learning. However, beyond linear regression, the theoretical advantage of full-batch gradient descent (GD, which always reuses all the data) over one-pass stochastic gradient descent (online SGD, which uses each data point only once) remains unclear. In this work, we consider learning a $d$-dimensional single-index model with a quadratic activation, for which it is known that one-pass SGD requires $n\gtrsim d\log d$ samples to achieve weak recovery. We first show that this $\log d$ factor in the sample complexity persists for full-batch spherical GD on the correlation loss; however, by simply truncating the activation, full-batch GD exhibits a favorable optimization landscape at $n \simeq d$ samples, thereby outperforming one-pass SGD (with the same activation) in statistical efficiency. We complement this result with a trajectory analysis of full-batch GD on the squared loss from small initialization, showing that $n \gtrsim d$ samples and $T \gtrsim\log d$ gradient steps suffice to achieve strong (exact) recovery.

A Law of Data Reconstruction for Random Features (and Beyond)

Large-scale deep learning models are known to memorize parts of the training set. In machine learning theory, memorization is often framed as interpolation or label fitting, and classical results show that this can be achieved when the number of parameters $p$ in the model is larger than the number of training samples $n$. In this work, we consider memorization from the perspective of data reconstruction, demonstrating that this can be achieved when $p$ is larger than $dn$, where $d$ is the dimensionality of the data. More specifically, we show that, in the random features model, when $p \gg dn$, the subspace spanned by the training samples in feature space gives sufficient information to identify the individual samples in input space. Our analysis suggests an optimization method to reconstruct the dataset from the model parameters, and we demonstrate that this method performs well on various architectures (random features, two-layer fully-connected and deep residual networks). Our results reveal a law of data reconstruction, according to which the entire training dataset can be recovered as $p$ exceeds the threshold $dn$.

Attention with Trained Embeddings Provably Selects Important Tokens

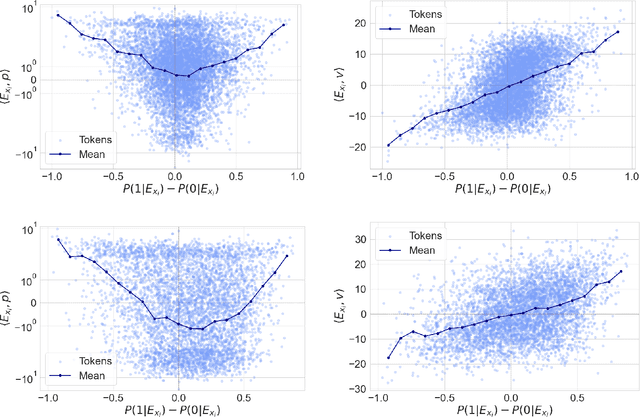
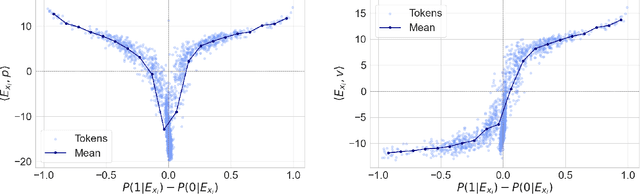
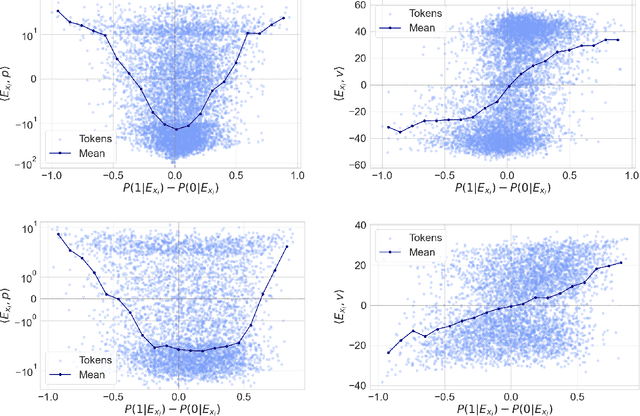
Token embeddings play a crucial role in language modeling but, despite this practical relevance, their theoretical understanding remains limited. Our paper addresses the gap by characterizing the structure of embeddings obtained via gradient descent. Specifically, we consider a one-layer softmax attention model with a linear head for binary classification, i.e., $\texttt{Softmax}( p^\top E_X^\top ) E_X v = \frac{ \sum_{i=1}^T \exp(p^\top E_{x_i}) E_{x_i}^\top v}{\sum_{j=1}^T \exp(p^\top E_{x_{j}}) }$, where $E_X = [ E_{x_1} , \dots, E_{x_T} ]^\top$ contains the embeddings of the input sequence, $p$ is the embedding of the $\mathrm{\langle cls \rangle}$ token and $v$ the output vector. First, we show that, already after a single step of gradient training with the logistic loss, the embeddings $E_X$ capture the importance of tokens in the dataset by aligning with the output vector $v$ proportionally to the frequency with which the corresponding tokens appear in the dataset. Then, after training $p$ via gradient flow until convergence, the softmax selects the important tokens in the sentence (i.e., those that are predictive of the label), and the resulting $\mathrm{\langle cls \rangle}$ embedding maximizes the margin for such a selection. Experiments on real-world datasets (IMDB, Yelp) exhibit a phenomenology close to that unveiled by our theory.

Better Rates for Private Linear Regression in the Proportional Regime via Aggressive Clipping

Differentially private (DP) linear regression has received significant attention in the recent theoretical literature, with several works aimed at obtaining improved error rates. A common approach is to set the clipping constant much larger than the expected norm of the per-sample gradients. While simplifying the analysis, this is however in sharp contrast with what empirical evidence suggests to optimize performance. Our work bridges this gap between theory and practice: we provide sharper rates for DP stochastic gradient descent (DP-SGD) by crucially operating in a regime where clipping happens frequently. Specifically, we consider the setting where the data is multivariate Gaussian, the number of training samples $n$ is proportional to the input dimension $d$, and the algorithm guarantees constant-order zero concentrated DP. Our method relies on establishing a deterministic equivalent for the trajectory of DP-SGD in terms of a family of ordinary differential equations (ODEs). As a consequence, the risk of DP-SGD is bounded between two ODEs, with upper and lower bounds matching for isotropic data. By studying these ODEs when $n / d$ is large enough, we demonstrate the optimality of aggressive clipping, and we uncover the benefits of decaying learning rate and private noise scheduling.

Neural Collapse is Globally Optimal in Deep Regularized ResNets and Transformers

The empirical emergence of neural collapse -- a surprising symmetry in the feature representations of the training data in the penultimate layer of deep neural networks -- has spurred a line of theoretical research aimed at its understanding. However, existing work focuses on data-agnostic models or, when data structure is taken into account, it remains limited to multi-layer perceptrons. Our paper fills both these gaps by analyzing modern architectures in a data-aware regime: we prove that global optima of deep regularized transformers and residual networks (ResNets) with LayerNorm trained with cross entropy or mean squared error loss are approximately collapsed, and the approximation gets tighter as the depth grows. More generally, we formally reduce any end-to-end large-depth ResNet or transformer training into an equivalent unconstrained features model, thus justifying its wide use in the literature even beyond data-agnostic settings. Our theoretical results are supported by experiments on computer vision and language datasets showing that, as the depth grows, neural collapse indeed becomes more prominent.

Test-Time Training Provably Improves Transformers as In-context Learners

Test-time training (TTT) methods explicitly update the weights of a model to adapt to the specific test instance, and they have found success in a variety of settings, including most recently language modeling and reasoning. To demystify this success, we investigate a gradient-based TTT algorithm for in-context learning, where we train a transformer model on the in-context demonstrations provided in the test prompt. Specifically, we provide a comprehensive theoretical characterization of linear transformers when the update rule is a single gradient step. Our theory (i) delineates the role of alignment between pretraining distribution and target task, (ii) demystifies how TTT can alleviate distribution shift, and (iii) quantifies the sample complexity of TTT including how it can significantly reduce the eventual sample size required for in-context learning. As our empirical contribution, we study the benefits of TTT for TabPFN, a tabular foundation model. In line with our theory, we demonstrate that TTT significantly reduces the required sample size for tabular classification (3 to 5 times fewer) unlocking substantial inference efficiency with a negligible training cost.

Spurious Correlations in High Dimensional Regression: The Roles of Regularization, Simplicity Bias and Over-Parameterization

Learning models have been shown to rely on spurious correlations between non-predictive features and the associated labels in the training data, with negative implications on robustness, bias and fairness. In this work, we provide a statistical characterization of this phenomenon for high-dimensional regression, when the data contains a predictive core feature $x$ and a spurious feature $y$. Specifically, we quantify the amount of spurious correlations $C$ learned via linear regression, in terms of the data covariance and the strength $\lambda$ of the ridge regularization. As a consequence, we first capture the simplicity of $y$ through the spectrum of its covariance, and its correlation with $x$ through the Schur complement of the full data covariance. Next, we prove a trade-off between $C$ and the in-distribution test loss $L$, by showing that the value of $\lambda$ that minimizes $L$ lies in an interval where $C$ is increasing. Finally, we investigate the effects of over-parameterization via the random features model, by showing its equivalence to regularized linear regression. Our theoretical results are supported by numerical experiments on Gaussian, Color-MNIST, and CIFAR-10 datasets.

Spectral Estimators for Multi-Index Models: Precise Asymptotics and Optimal Weak Recovery

Multi-index models provide a popular framework to investigate the learnability of functions with low-dimensional structure and, also due to their connections with neural networks, they have been object of recent intensive study. In this paper, we focus on recovering the subspace spanned by the signals via spectral estimators -- a family of methods that are routinely used in practice, often as a warm-start for iterative algorithms. Our main technical contribution is a precise asymptotic characterization of the performance of spectral methods, when sample size and input dimension grow proportionally and the dimension $p$ of the space to recover is fixed. Specifically, we locate the top-$p$ eigenvalues of the spectral matrix and establish the overlaps between the corresponding eigenvectors (which give the spectral estimators) and a basis of the signal subspace. Our analysis unveils a phase transition phenomenon in which, as the sample complexity grows, eigenvalues escape from the bulk of the spectrum and, when that happens, eigenvectors recover directions of the desired subspace. The precise characterization we put forward enables the optimization of the data preprocessing, thus allowing to identify the spectral estimator that requires the minimal sample size for weak recovery.