Diyuan Wu
Attention with Trained Embeddings Provably Selects Important Tokens
May 22, 2025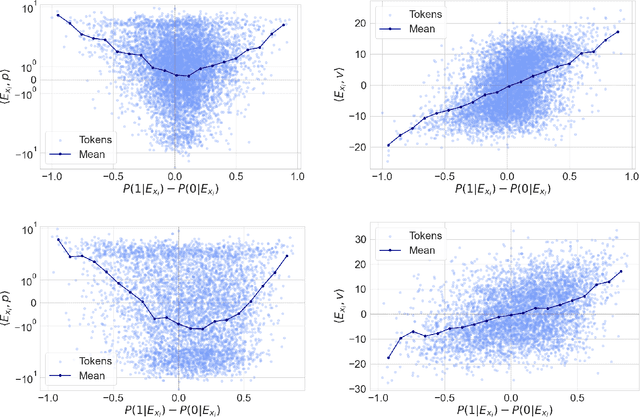
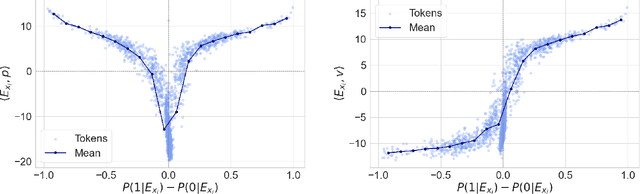
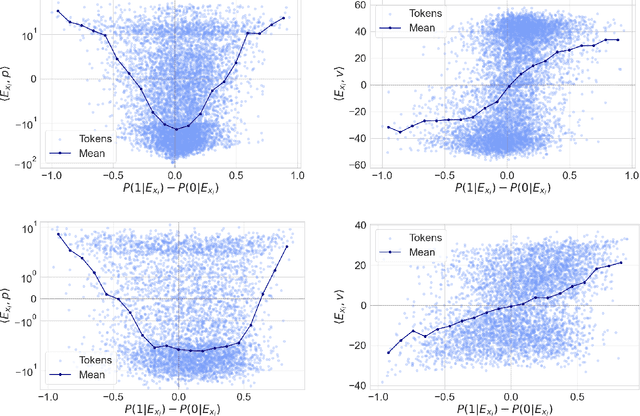
Abstract:Token embeddings play a crucial role in language modeling but, despite this practical relevance, their theoretical understanding remains limited. Our paper addresses the gap by characterizing the structure of embeddings obtained via gradient descent. Specifically, we consider a one-layer softmax attention model with a linear head for binary classification, i.e., $\texttt{Softmax}( p^\top E_X^\top ) E_X v = \frac{ \sum_{i=1}^T \exp(p^\top E_{x_i}) E_{x_i}^\top v}{\sum_{j=1}^T \exp(p^\top E_{x_{j}}) }$, where $E_X = [ E_{x_1} , \dots, E_{x_T} ]^\top$ contains the embeddings of the input sequence, $p$ is the embedding of the $\mathrm{\langle cls \rangle}$ token and $v$ the output vector. First, we show that, already after a single step of gradient training with the logistic loss, the embeddings $E_X$ capture the importance of tokens in the dataset by aligning with the output vector $v$ proportionally to the frequency with which the corresponding tokens appear in the dataset. Then, after training $p$ via gradient flow until convergence, the softmax selects the important tokens in the sentence (i.e., those that are predictive of the label), and the resulting $\mathrm{\langle cls \rangle}$ embedding maximizes the margin for such a selection. Experiments on real-world datasets (IMDB, Yelp) exhibit a phenomenology close to that unveiled by our theory.
Neural Collapse Beyond the Unconstrainted Features Model: Landscape, Dynamics, and Generalization in the Mean-Field Regime
Jan 31, 2025Abstract:Neural Collapse is a phenomenon where the last-layer representations of a well-trained neural network converge to a highly structured geometry. In this paper, we focus on its first (and most basic) property, known as NC1: the within-class variability vanishes. While prior theoretical studies establish the occurrence of NC1 via the data-agnostic unconstrained features model, our work adopts a data-specific perspective, analyzing NC1 in a three-layer neural network, with the first two layers operating in the mean-field regime and followed by a linear layer. In particular, we establish a fundamental connection between NC1 and the loss landscape: we prove that points with small empirical loss and gradient norm (thus, close to being stationary) approximately satisfy NC1, and the closeness to NC1 is controlled by the residual loss and gradient norm. We then show that (i) gradient flow on the mean squared error converges to NC1 solutions with small empirical loss, and (ii) for well-separated data distributions, both NC1 and vanishing test loss are achieved simultaneously. This aligns with the empirical observation that NC1 emerges during training while models attain near-zero test error. Overall, our results demonstrate that NC1 arises from gradient training due to the properties of the loss landscape, and they show the co-occurrence of NC1 and small test error for certain data distributions.
The Iterative Optimal Brain Surgeon: Faster Sparse Recovery by Leveraging Second-Order Information
Aug 30, 2024Abstract:The rising footprint of machine learning has led to a focus on imposing \emph{model sparsity} as a means of reducing computational and memory costs. For deep neural networks (DNNs), the state-of-the-art accuracy-vs-sparsity is achieved by heuristics inspired by the classical Optimal Brain Surgeon (OBS) framework~\citep{lecun90brain, hassibi1992second, hassibi1993optimal}, which leverages loss curvature information to make better pruning decisions. Yet, these results still lack a solid theoretical understanding, and it is unclear whether they can be improved by leveraging connections to the wealth of work on sparse recovery algorithms. In this paper, we draw new connections between these two areas and present new sparse recovery algorithms inspired by the OBS framework that comes with theoretical guarantees under reasonable assumptions and have strong practical performance. Specifically, our work starts from the observation that we can leverage curvature information in OBS-like fashion upon the projection step of classic iterative sparse recovery algorithms such as IHT. We show for the first time that this leads both to improved convergence bounds under standard assumptions. Furthermore, we present extensions of this approach to the practical task of obtaining accurate sparse DNNs, and validate it experimentally at scale for Transformer-based models on vision and language tasks.
Mean-field analysis for heavy ball methods: Dropout-stability, connectivity, and global convergence
Oct 13, 2022Abstract:The stochastic heavy ball method (SHB), also known as stochastic gradient descent (SGD) with Polyak's momentum, is widely used in training neural networks. However, despite the remarkable success of such algorithm in practice, its theoretical characterization remains limited. In this paper, we focus on neural networks with two and three layers and provide a rigorous understanding of the properties of the solutions found by SHB: \emph{(i)} stability after dropping out part of the neurons, \emph{(ii)} connectivity along a low-loss path, and \emph{(iii)} convergence to the global optimum. To achieve this goal, we take a mean-field view and relate the SHB dynamics to a certain partial differential equation in the limit of large network widths. This mean-field perspective has inspired a recent line of work focusing on SGD while, in contrast, our paper considers an algorithm with momentum. More specifically, after proving existence and uniqueness of the limit differential equations, we show convergence to the global optimum and give a quantitative bound between the mean-field limit and the SHB dynamics of a finite-width network. Armed with this last bound, we are able to establish the dropout-stability and connectivity of SHB solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge