Wide Neural Networks Trained with Weight Decay Provably Exhibit Neural Collapse

Deep neural networks (DNNs) at convergence consistently represent the training data in the last layer via a highly symmetric geometric structure referred to as neural collapse. This empirical evidence has spurred a line of theoretical research aimed at proving the emergence of neural collapse, mostly focusing on the unconstrained features model. Here, the features of the penultimate layer are free variables, which makes the model data-agnostic and, hence, puts into question its ability to capture DNN training. Our work addresses the issue, moving away from unconstrained features and studying DNNs that end with at least two linear layers. We first prove generic guarantees on neural collapse that assume (i) low training error and balancedness of the linear layers (for within-class variability collapse), and (ii) bounded conditioning of the features before the linear part (for orthogonality of class-means, as well as their alignment with weight matrices). We then show that such assumptions hold for gradient descent training with weight decay: (i) for networks with a wide first layer, we prove low training error and balancedness, and (ii) for solutions that are either nearly optimal or stable under large learning rates, we additionally prove the bounded conditioning. Taken together, our results are the first to show neural collapse in the end-to-end training of DNNs.

Neural Collapse versus Low-rank Bias: Is Deep Neural Collapse Really Optimal?

Deep neural networks (DNNs) exhibit a surprising structure in their final layer known as neural collapse (NC), and a growing body of works has currently investigated the propagation of neural collapse to earlier layers of DNNs -- a phenomenon called deep neural collapse (DNC). However, existing theoretical results are restricted to special cases: linear models, only two layers or binary classification. In contrast, we focus on non-linear models of arbitrary depth in multi-class classification and reveal a surprising qualitative shift. As soon as we go beyond two layers or two classes, DNC stops being optimal for the deep unconstrained features model (DUFM) -- the standard theoretical framework for the analysis of collapse. The main culprit is a low-rank bias of multi-layer regularization schemes: this bias leads to optimal solutions of even lower rank than the neural collapse. We support our theoretical findings with experiments on both DUFM and real data, which show the emergence of the low-rank structure in the solution found by gradient descent.

Average gradient outer product as a mechanism for deep neural collapse

Deep Neural Collapse (DNC) refers to the surprisingly rigid structure of the data representations in the final layers of Deep Neural Networks (DNNs). Though the phenomenon has been measured in a wide variety of settings, its emergence is only partially understood. In this work, we provide substantial evidence that DNC formation occurs primarily through deep feature learning with the average gradient outer product (AGOP). This takes a step further compared to efforts that explain neural collapse via feature-agnostic approaches, such as the unconstrained features model. We proceed by providing evidence that the right singular vectors and values of the weights are responsible for the majority of within-class variability collapse in DNNs. As shown in recent work, this singular structure is highly correlated with that of the AGOP. We then establish experimentally and theoretically that AGOP induces neural collapse in a randomly initialized neural network. In particular, we demonstrate that Deep Recursive Feature Machines, a method originally introduced as an abstraction for AGOP feature learning in convolutional neural networks, exhibits DNC.

Deep Neural Collapse Is Provably Optimal for the Deep Unconstrained Features Model

Neural collapse (NC) refers to the surprising structure of the last layer of deep neural networks in the terminal phase of gradient descent training. Recently, an increasing amount of experimental evidence has pointed to the propagation of NC to earlier layers of neural networks. However, while the NC in the last layer is well studied theoretically, much less is known about its multi-layered counterpart - deep neural collapse (DNC). In particular, existing work focuses either on linear layers or only on the last two layers at the price of an extra assumption. Our paper fills this gap by generalizing the established analytical framework for NC - the unconstrained features model - to multiple non-linear layers. Our key technical contribution is to show that, in a deep unconstrained features model, the unique global optimum for binary classification exhibits all the properties typical of DNC. This explains the existing experimental evidence of DNC. We also empirically show that (i) by optimizing deep unconstrained features models via gradient descent, the resulting solution agrees well with our theory, and (ii) trained networks recover the unconstrained features suitable for the occurrence of DNC, thus supporting the validity of this modeling principle.

The Unreasonable Effectiveness of Fully-Connected Layers for Low-Data Regimes

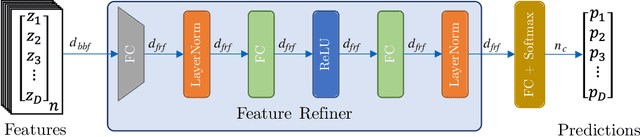
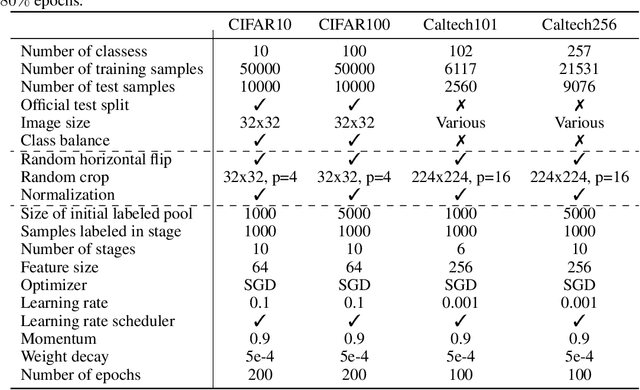
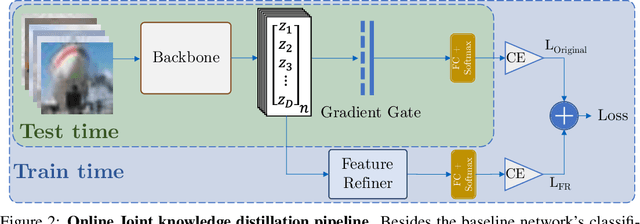
Convolutional neural networks were the standard for solving many computer vision tasks until recently, when Transformers of MLP-based architectures have started to show competitive performance. These architectures typically have a vast number of weights and need to be trained on massive datasets; hence, they are not suitable for their use in low-data regimes. In this work, we propose a simple yet effective framework to improve generalization from small amounts of data. We augment modern CNNs with fully-connected (FC) layers and show the massive impact this architectural change has in low-data regimes. We further present an online joint knowledge-distillation method to utilize the extra FC layers at train time but avoid them during test time. This allows us to improve the generalization of a CNN-based model without any increase in the number of weights at test time. We perform classification experiments for a large range of network backbones and several standard datasets on supervised learning and active learning. Our experiments significantly outperform the networks without fully-connected layers, reaching a relative improvement of up to $16\%$ validation accuracy in the supervised setting without adding any extra parameters during inference.

Generalization In Multi-Objective Machine Learning

Modern machine learning tasks often require considering not just one but multiple objectives. For example, besides the prediction quality, this could be the efficiency, robustness or fairness of the learned models, or any of their combinations. Multi-objective learning offers a natural framework for handling such problems without having to commit to early trade-offs. Surprisingly, statistical learning theory so far offers almost no insight into the generalization properties of multi-objective learning. In this work, we make first steps to fill this gap: we establish foundational generalization bounds for the multi-objective setting as well as generalization and excess bounds for learning with scalarizations. We also provide the first theoretical analysis of the relation between the Pareto-optimal sets of the true objectives and the Pareto-optimal sets of their empirical approximations from training data. In particular, we show a surprising asymmetry: all Pareto-optimal solutions can be approximated by empirically Pareto-optimal ones, but not vice versa.

Intriguing Properties of Input-dependent Randomized Smoothing

Randomized smoothing is currently considered the state-of-the-art method to obtain certifiably robust classifiers. Despite its remarkable performance, the method is associated with various serious problems such as ``certified accuracy waterfalls'', certification vs. accuracy trade-off, or even fairness issues. Input-dependent smoothing approaches have been proposed to overcome these flaws. However, we demonstrate that these methods lack formal guarantees and so the resulting certificates are not justified. We show that the input-dependent smoothing, in general, suffers from the curse of dimensionality, forcing the variance function to have low semi-elasticity. On the other hand, we provide a theoretical and practical framework that enables the usage of input-dependent smoothing even in the presence of the curse of dimensionality, under strict restrictions. We present one concrete design of the smoothing variance and test it on CIFAR10 and MNIST. Our design solves some of the problems of classical smoothing and is formally underlined, yet further improvement of the design is still necessary.