A Gap Between the Gaussian RKHS and Neural Networks: An Infinite-Center Asymptotic Analysis

Recent works have characterized the function-space inductive bias of infinite-width bounded-norm single-hidden-layer neural networks as a kind of bounded-variation-type space. This novel neural network Banach space encompasses many classical multivariate function spaces including certain Sobolev spaces and the spectral Barron spaces. Notably, this Banach space also includes functions that exhibit less classical regularity such as those that only vary in a few directions. On bounded domains, it is well-established that the Gaussian reproducing kernel Hilbert space (RKHS) strictly embeds into this Banach space, demonstrating a clear gap between the Gaussian RKHS and the neural network Banach space. It turns out that when investigating these spaces on unbounded domains, e.g., all of $\mathbb{R}^d$, the story is fundamentally different. We establish the following fundamental result: Certain functions that lie in the Gaussian RKHS have infinite norm in the neural network Banach space. This provides a nontrivial gap between kernel methods and neural networks by the exhibition of functions in which kernel methods can do strictly better than neural networks.

Task Generalization With AutoRegressive Compositional Structure: Can Learning From $\d$ Tasks Generalize to $\d^{T}$ Tasks?

Large language models (LLMs) exhibit remarkable task generalization, solving tasks they were never explicitly trained on with only a few demonstrations. This raises a fundamental question: When can learning from a small set of tasks generalize to a large task family? In this paper, we investigate task generalization through the lens of AutoRegressive Compositional (ARC) structure, where each task is a composition of $T$ operations, and each operation is among a finite family of $\d$ subtasks. This yields a total class of size~\( \d^\TT \). We first show that generalization to all \( \d^\TT \) tasks is theoretically achievable by training on only \( \tilde{O}(\d) \) tasks. Empirically, we demonstrate that Transformers achieve such exponential task generalization on sparse parity functions via in-context learning (ICL) and Chain-of-Thought (CoT) reasoning. We further demonstrate this generalization in arithmetic and language translation, extending beyond parity functions.

Aggregate and conquer: detecting and steering LLM concepts by combining nonlinear predictors over multiple layers

A trained Large Language Model (LLM) contains much of human knowledge. Yet, it is difficult to gauge the extent or accuracy of that knowledge, as LLMs do not always ``know what they know'' and may even be actively misleading. In this work, we give a general method for detecting semantic concepts in the internal activations of LLMs. Furthermore, we show that our methodology can be easily adapted to steer LLMs toward desirable outputs. Our innovations are the following: (1) we use a nonlinear feature learning method to identify important linear directions for predicting concepts from each layer; (2) we aggregate features across layers to build powerful concept detectors and steering mechanisms. We showcase the power of our approach by attaining state-of-the-art results for detecting hallucinations, harmfulness, toxicity, and untruthful content on seven benchmarks. We highlight the generality of our approach by steering LLMs towards new concepts that, to the best of our knowledge, have not been previously considered in the literature, including: semantic disambiguation, human languages, programming languages, hallucinated responses, science subjects, poetic/Shakespearean English, and even multiple concepts simultaneously. Moreover, our method can steer concepts with numerical attributes such as product reviews. We provide our code (including a simple API for our methods) at https://github.com/dmbeaglehole/neural_controllers .

Fast training of large kernel models with delayed projections

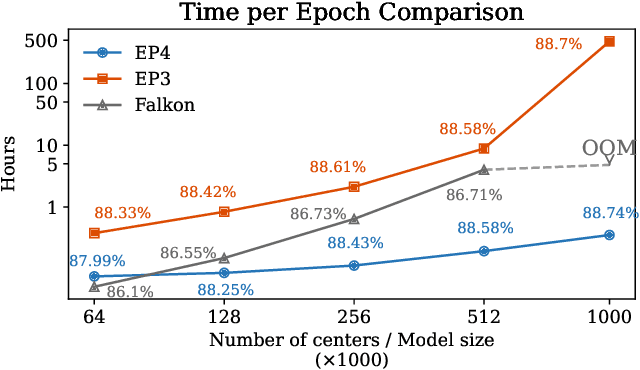
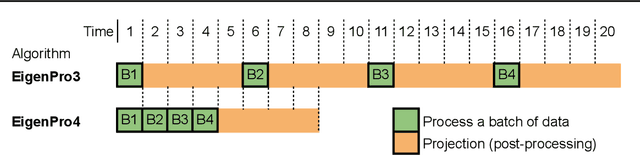
Classical kernel machines have historically faced significant challenges in scaling to large datasets and model sizes--a key ingredient that has driven the success of neural networks. In this paper, we present a new methodology for building kernel machines that can scale efficiently with both data size and model size. Our algorithm introduces delayed projections to Preconditioned Stochastic Gradient Descent (PSGD) allowing the training of much larger models than was previously feasible, pushing the practical limits of kernel-based learning. We validate our algorithm, EigenPro4, across multiple datasets, demonstrating drastic training speed up over the existing methods while maintaining comparable or better classification accuracy.

Mirror Descent on Reproducing Kernel Banach Spaces

Recent advances in machine learning have led to increased interest in reproducing kernel Banach spaces (RKBS) as a more general framework that extends beyond reproducing kernel Hilbert spaces (RKHS). These works have resulted in the formulation of representer theorems under several regularized learning schemes. However, little is known about an optimization method that encompasses these results in this setting. This paper addresses a learning problem on Banach spaces endowed with a reproducing kernel, focusing on efficient optimization within RKBS. To tackle this challenge, we propose an algorithm based on mirror descent (MDA). Our approach involves an iterative method that employs gradient steps in the dual space of the Banach space using the reproducing kernel. We analyze the convergence properties of our algorithm under various assumptions and establish two types of results: first, we identify conditions under which a linear convergence rate is achievable, akin to optimization in the Euclidean setting, and provide a proof of the linear rate; second, we demonstrate a standard convergence rate in a constrained setting. Moreover, to instantiate this algorithm in practice, we introduce a novel family of RKBSs with $p$-norm ($p \neq 2$), characterized by both an explicit dual map and a kernel.

Context-Scaling versus Task-Scaling in In-Context Learning

Transformers exhibit In-Context Learning (ICL), where these models solve new tasks by using examples in the prompt without additional training. In our work, we identify and analyze two key components of ICL: (1) context-scaling, where model performance improves as the number of in-context examples increases and (2) task-scaling, where model performance improves as the number of pre-training tasks increases. While transformers are capable of both context-scaling and task-scaling, we empirically show that standard Multi-Layer Perceptrons (MLPs) with vectorized input are only capable of task-scaling. To understand how transformers are capable of context-scaling, we first propose a significantly simplified transformer architecture without key, query, value weights. We show that it performs ICL comparably to the original GPT-2 model in various statistical learning tasks including linear regression, teacher-student settings. Furthermore, a single block of our simplified transformer can be viewed as data dependent feature map followed by an MLP. This feature map on its own is a powerful predictor that is capable of context-scaling but is not capable of task-scaling. We show empirically that concatenating the output of this feature map with vectorized data as an input to MLPs enables both context-scaling and task-scaling. This finding provides a simple setting to study context and task-scaling for ICL.

Emergence in non-neural models: grokking modular arithmetic via average gradient outer product

Neural networks trained to solve modular arithmetic tasks exhibit grokking, a phenomenon where the test accuracy starts improving long after the model achieves 100% training accuracy in the training process. It is often taken as an example of "emergence", where model ability manifests sharply through a phase transition. In this work, we show that the phenomenon of grokking is not specific to neural networks nor to gradient descent-based optimization. Specifically, we show that this phenomenon occurs when learning modular arithmetic with Recursive Feature Machines (RFM), an iterative algorithm that uses the Average Gradient Outer Product (AGOP) to enable task-specific feature learning with general machine learning models. When used in conjunction with kernel machines, iterating RFM results in a fast transition from random, near zero, test accuracy to perfect test accuracy. This transition cannot be predicted from the training loss, which is identically zero, nor from the test loss, which remains constant in initial iterations. Instead, as we show, the transition is completely determined by feature learning: RFM gradually learns block-circulant features to solve modular arithmetic. Paralleling the results for RFM, we show that neural networks that solve modular arithmetic also learn block-circulant features. Furthermore, we present theoretical evidence that RFM uses such block-circulant features to implement the Fourier Multiplication Algorithm, which prior work posited as the generalizing solution neural networks learn on these tasks. Our results demonstrate that emergence can result purely from learning task-relevant features and is not specific to neural architectures nor gradient descent-based optimization methods. Furthermore, our work provides more evidence for AGOP as a key mechanism for feature learning in neural networks.

Average gradient outer product as a mechanism for deep neural collapse

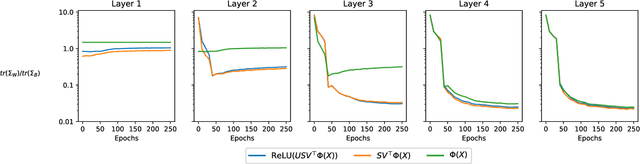
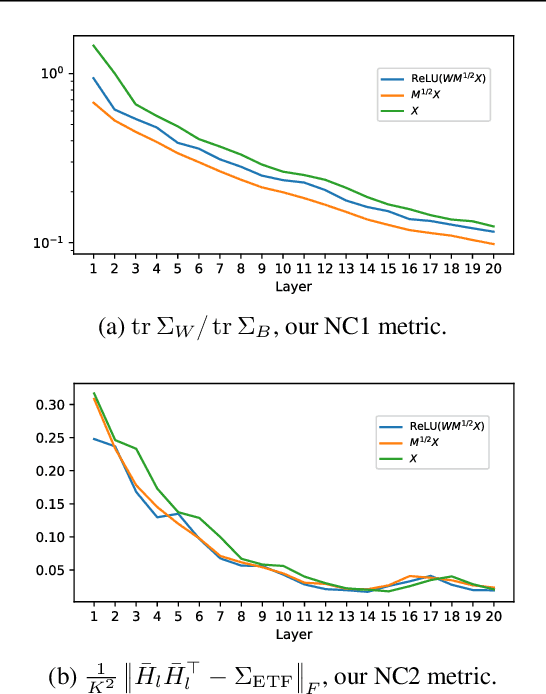
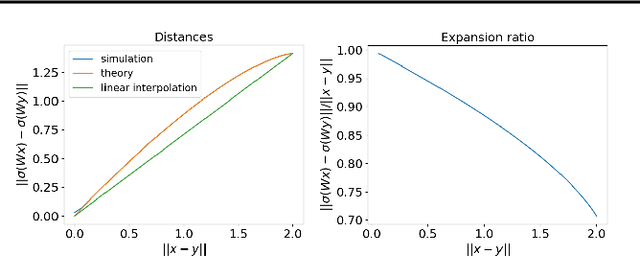
Deep Neural Collapse (DNC) refers to the surprisingly rigid structure of the data representations in the final layers of Deep Neural Networks (DNNs). Though the phenomenon has been measured in a wide variety of settings, its emergence is only partially understood. In this work, we provide substantial evidence that DNC formation occurs primarily through deep feature learning with the average gradient outer product (AGOP). This takes a step further compared to efforts that explain neural collapse via feature-agnostic approaches, such as the unconstrained features model. We proceed by providing evidence that the right singular vectors and values of the weights are responsible for the majority of within-class variability collapse in DNNs. As shown in recent work, this singular structure is highly correlated with that of the AGOP. We then establish experimentally and theoretically that AGOP induces neural collapse in a randomly initialized neural network. In particular, we demonstrate that Deep Recursive Feature Machines, a method originally introduced as an abstraction for AGOP feature learning in convolutional neural networks, exhibits DNC.

Unmemorization in Large Language Models via Self-Distillation and Deliberate Imagination

While displaying impressive generation capabilities across many tasks, Large Language Models (LLMs) still struggle with crucial issues of privacy violation and unwanted exposure of sensitive data. This raises an essential question: how should we prevent such undesired behavior of LLMs while maintaining their strong generation and natural language understanding (NLU) capabilities? In this work, we introduce a novel approach termed deliberate imagination in the context of LLM unlearning. Instead of trying to forget memorized data, we employ a self-distillation framework, guiding LLMs to deliberately imagine alternative scenarios. As demonstrated in a wide range of experiments, the proposed method not only effectively unlearns targeted text but also preserves the LLMs' capabilities in open-ended generation tasks as well as in NLU tasks. Our results demonstrate the usefulness of this approach across different models and sizes, and also with parameter-efficient fine-tuning, offering a novel pathway to addressing the challenges with private and sensitive data in LLM applications.

Linear Recursive Feature Machines provably recover low-rank matrices

A fundamental problem in machine learning is to understand how neural networks make accurate predictions, while seemingly bypassing the curse of dimensionality. A possible explanation is that common training algorithms for neural networks implicitly perform dimensionality reduction - a process called feature learning. Recent work posited that the effects of feature learning can be elicited from a classical statistical estimator called the average gradient outer product (AGOP). The authors proposed Recursive Feature Machines (RFMs) as an algorithm that explicitly performs feature learning by alternating between (1) reweighting the feature vectors by the AGOP and (2) learning the prediction function in the transformed space. In this work, we develop the first theoretical guarantees for how RFM performs dimensionality reduction by focusing on the class of overparametrized problems arising in sparse linear regression and low-rank matrix recovery. Specifically, we show that RFM restricted to linear models (lin-RFM) generalizes the well-studied Iteratively Reweighted Least Squares (IRLS) algorithm. Our results shed light on the connection between feature learning in neural networks and classical sparse recovery algorithms. In addition, we provide an implementation of lin-RFM that scales to matrices with millions of missing entries. Our implementation is faster than the standard IRLS algorithm as it is SVD-free. It also outperforms deep linear networks for sparse linear regression and low-rank matrix completion.