Feature maps for the Laplacian kernel and its generalizations

Recent applications of kernel methods in machine learning have seen a renewed interest in the Laplacian kernel, due to its stability to the bandwidth hyperparameter in comparison to the Gaussian kernel, as well as its expressivity being equivalent to that of the neural tangent kernel of deep fully connected networks. However, unlike the Gaussian kernel, the Laplacian kernel is not separable. This poses challenges for techniques to approximate it, especially via the random Fourier features (RFF) methodology and its variants. In this work, we provide random features for the Laplacian kernel and its two generalizations: Mat\'{e}rn kernel and the Exponential power kernel. We provide efficiently implementable schemes to sample weight matrices so that random features approximate these kernels. These weight matrices have a weakly coupled heavy-tailed randomness. Via numerical experiments on real datasets we demonstrate the efficacy of these random feature maps.

Fast training of large kernel models with delayed projections

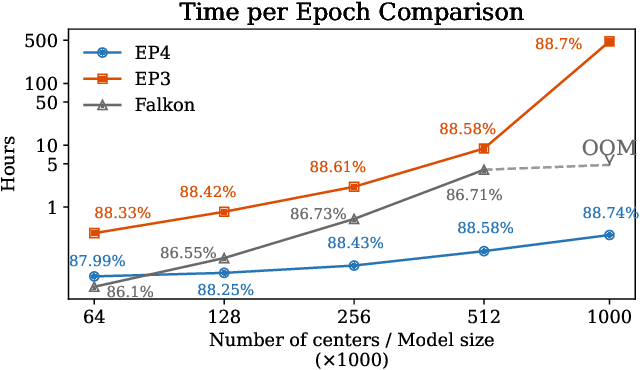
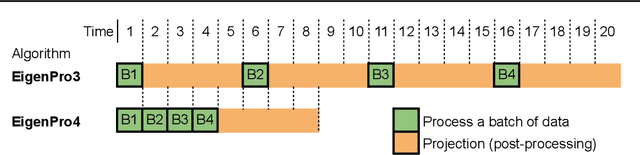
Classical kernel machines have historically faced significant challenges in scaling to large datasets and model sizes--a key ingredient that has driven the success of neural networks. In this paper, we present a new methodology for building kernel machines that can scale efficiently with both data size and model size. Our algorithm introduces delayed projections to Preconditioned Stochastic Gradient Descent (PSGD) allowing the training of much larger models than was previously feasible, pushing the practical limits of kernel-based learning. We validate our algorithm, EigenPro4, across multiple datasets, demonstrating drastic training speed up over the existing methods while maintaining comparable or better classification accuracy.

Mirror Descent on Reproducing Kernel Banach Spaces

Recent advances in machine learning have led to increased interest in reproducing kernel Banach spaces (RKBS) as a more general framework that extends beyond reproducing kernel Hilbert spaces (RKHS). These works have resulted in the formulation of representer theorems under several regularized learning schemes. However, little is known about an optimization method that encompasses these results in this setting. This paper addresses a learning problem on Banach spaces endowed with a reproducing kernel, focusing on efficient optimization within RKBS. To tackle this challenge, we propose an algorithm based on mirror descent (MDA). Our approach involves an iterative method that employs gradient steps in the dual space of the Banach space using the reproducing kernel. We analyze the convergence properties of our algorithm under various assumptions and establish two types of results: first, we identify conditions under which a linear convergence rate is achievable, akin to optimization in the Euclidean setting, and provide a proof of the linear rate; second, we demonstrate a standard convergence rate in a constrained setting. Moreover, to instantiate this algorithm in practice, we introduce a novel family of RKBSs with $p$-norm ($p \neq 2$), characterized by both an explicit dual map and a kernel.

Universality of kernel random matrices and kernel regression in the quadratic regime

Kernel ridge regression (KRR) is a popular class of machine learning models that has become an important tool for understanding deep learning. Much of the focus has been on studying the proportional asymptotic regime, $n \asymp d$, where $n$ is the number of training samples and $d$ is the dimension of the dataset. In this regime, under certain conditions on the data distribution, the kernel random matrix involved in KRR exhibits behavior akin to that of a linear kernel. In this work, we extend the study of kernel regression to the quadratic asymptotic regime, where $n \asymp d^2$. In this regime, we demonstrate that a broad class of inner-product kernels exhibit behavior similar to a quadratic kernel. Specifically, we establish an operator norm approximation bound for the difference between the original kernel random matrix and a quadratic kernel random matrix with additional correction terms compared to the Taylor expansion of the kernel functions. The approximation works for general data distributions under a Gaussian-moment-matching assumption with a covariance structure. This new approximation is utilized to obtain a limiting spectral distribution of the original kernel matrix and characterize the precise asymptotic training and generalization errors for KRR in the quadratic regime when $n/d^2$ converges to a non-zero constant. The generalization errors are obtained for both deterministic and random teacher models. Our proof techniques combine moment methods, Wick's formula, orthogonal polynomials, and resolvent analysis of random matrices with correlated entries.

Emergence in non-neural models: grokking modular arithmetic via average gradient outer product

Neural networks trained to solve modular arithmetic tasks exhibit grokking, a phenomenon where the test accuracy starts improving long after the model achieves 100% training accuracy in the training process. It is often taken as an example of "emergence", where model ability manifests sharply through a phase transition. In this work, we show that the phenomenon of grokking is not specific to neural networks nor to gradient descent-based optimization. Specifically, we show that this phenomenon occurs when learning modular arithmetic with Recursive Feature Machines (RFM), an iterative algorithm that uses the Average Gradient Outer Product (AGOP) to enable task-specific feature learning with general machine learning models. When used in conjunction with kernel machines, iterating RFM results in a fast transition from random, near zero, test accuracy to perfect test accuracy. This transition cannot be predicted from the training loss, which is identically zero, nor from the test loss, which remains constant in initial iterations. Instead, as we show, the transition is completely determined by feature learning: RFM gradually learns block-circulant features to solve modular arithmetic. Paralleling the results for RFM, we show that neural networks that solve modular arithmetic also learn block-circulant features. Furthermore, we present theoretical evidence that RFM uses such block-circulant features to implement the Fourier Multiplication Algorithm, which prior work posited as the generalizing solution neural networks learn on these tasks. Our results demonstrate that emergence can result purely from learning task-relevant features and is not specific to neural architectures nor gradient descent-based optimization methods. Furthermore, our work provides more evidence for AGOP as a key mechanism for feature learning in neural networks.

On the Nystrom Approximation for Preconditioning in Kernel Machines

Kernel methods are a popular class of nonlinear predictive models in machine learning. Scalable algorithms for learning kernel models need to be iterative in nature, but convergence can be slow due to poor conditioning. Spectral preconditioning is an important tool to speed-up the convergence of such iterative algorithms for training kernel models. However computing and storing a spectral preconditioner can be expensive which can lead to large computational and storage overheads, precluding the application of kernel methods to problems with large datasets. A Nystrom approximation of the spectral preconditioner is often cheaper to compute and store, and has demonstrated success in practical applications. In this paper we analyze the trade-offs of using such an approximated preconditioner. Specifically, we show that a sample of logarithmic size (as a function of the size of the dataset) enables the Nystrom-based approximated preconditioner to accelerate gradient descent nearly as well as the exact preconditioner, while also reducing the computational and storage overheads.

Mechanism of feature learning in convolutional neural networks

Understanding the mechanism of how convolutional neural networks learn features from image data is a fundamental problem in machine learning and computer vision. In this work, we identify such a mechanism. We posit the Convolutional Neural Feature Ansatz, which states that covariances of filters in any convolutional layer are proportional to the average gradient outer product (AGOP) taken with respect to patches of the input to that layer. We present extensive empirical evidence for our ansatz, including identifying high correlation between covariances of filters and patch-based AGOPs for convolutional layers in standard neural architectures, such as AlexNet, VGG, and ResNets pre-trained on ImageNet. We also provide supporting theoretical evidence. We then demonstrate the generality of our result by using the patch-based AGOP to enable deep feature learning in convolutional kernel machines. We refer to the resulting algorithm as (Deep) ConvRFM and show that our algorithm recovers similar features to deep convolutional networks including the notable emergence of edge detectors. Moreover, we find that Deep ConvRFM overcomes previously identified limitations of convolutional kernels, such as their inability to adapt to local signals in images and, as a result, leads to sizable performance improvement over fixed convolutional kernels.

Local Convergence of Gradient Descent-Ascent for Training Generative Adversarial Networks

Generative Adversarial Networks (GANs) are a popular formulation to train generative models for complex high dimensional data. The standard method for training GANs involves a gradient descent-ascent (GDA) procedure on a minimax optimization problem. This procedure is hard to analyze in general due to the nonlinear nature of the dynamics. We study the local dynamics of GDA for training a GAN with a kernel-based discriminator. This convergence analysis is based on a linearization of a non-linear dynamical system that describes the GDA iterations, under an \textit{isolated points model} assumption from [Becker et al. 2022]. Our analysis brings out the effect of the learning rates, regularization, and the bandwidth of the kernel discriminator, on the local convergence rate of GDA. Importantly, we show phase transitions that indicate when the system converges, oscillates, or diverges. We also provide numerical simulations that verify our claims.

Toward Large Kernel Models

Recent studies indicate that kernel machines can often perform similarly or better than deep neural networks (DNNs) on small datasets. The interest in kernel machines has been additionally bolstered by the discovery of their equivalence to wide neural networks in certain regimes. However, a key feature of DNNs is their ability to scale the model size and training data size independently, whereas in traditional kernel machines model size is tied to data size. Because of this coupling, scaling kernel machines to large data has been computationally challenging. In this paper, we provide a way forward for constructing large-scale general kernel models, which are a generalization of kernel machines that decouples the model and data, allowing training on large datasets. Specifically, we introduce EigenPro 3.0, an algorithm based on projected dual preconditioned SGD and show scaling to model and data sizes which have not been possible with existing kernel methods.

Feature learning in neural networks and kernel machines that recursively learn features

Neural networks have achieved impressive results on many technological and scientific tasks. Yet, their empirical successes have outpaced our fundamental understanding of their structure and function. By identifying mechanisms driving the successes of neural networks, we can provide principled approaches for improving neural network performance and develop simple and effective alternatives. In this work, we isolate the key mechanism driving feature learning in fully connected neural networks by connecting neural feature learning to the average gradient outer product. We subsequently leverage this mechanism to design \textit{Recursive Feature Machines} (RFMs), which are kernel machines that learn features. We show that RFMs (1) accurately capture features learned by deep fully connected neural networks, (2) close the gap between kernel machines and fully connected networks, and (3) surpass a broad spectrum of models including neural networks on tabular data. Furthermore, we demonstrate that RFMs shed light on recently observed deep learning phenomena such as grokking, lottery tickets, simplicity biases, and spurious features. We provide a Python implementation to make our method broadly accessible [\href{https://github.com/aradha/recursive_feature_machines}{GitHub}].