On the Nystrom Approximation for Preconditioning in Kernel Machines

Kernel methods are a popular class of nonlinear predictive models in machine learning. Scalable algorithms for learning kernel models need to be iterative in nature, but convergence can be slow due to poor conditioning. Spectral preconditioning is an important tool to speed-up the convergence of such iterative algorithms for training kernel models. However computing and storing a spectral preconditioner can be expensive which can lead to large computational and storage overheads, precluding the application of kernel methods to problems with large datasets. A Nystrom approximation of the spectral preconditioner is often cheaper to compute and store, and has demonstrated success in practical applications. In this paper we analyze the trade-offs of using such an approximated preconditioner. Specifically, we show that a sample of logarithmic size (as a function of the size of the dataset) enables the Nystrom-based approximated preconditioner to accelerate gradient descent nearly as well as the exact preconditioner, while also reducing the computational and storage overheads.

Overcomplete order-3 tensor decomposition, blind deconvolution and Gaussian mixture models

We expand the family of tensors that can be efficiently decomposed and apply our new algorithmic ideas to blind deconvolution and Gaussian mixture models. Our basic contribution is an efficient algorithm to decompose certain symmetric overcomplete order-3 tensors, that is, three dimensional arrays of the form $T = \sum_{i=1}^n a_i \otimes a_i \otimes a_i$ where the $a_i$s are not linearly independent. Our second contribution builds on top of our tensor decomposition algorithm to expand the family of Gaussian mixture models whose parameters can be estimated efficiently. These ideas are also presented in a much more general framework of blind deconvolution that makes them applicable to mixture models of identical but very general distributions, including all centrally symmetric distributions with finite 6th moment.

Eigenvectors of Orthogonally Decomposable Functions

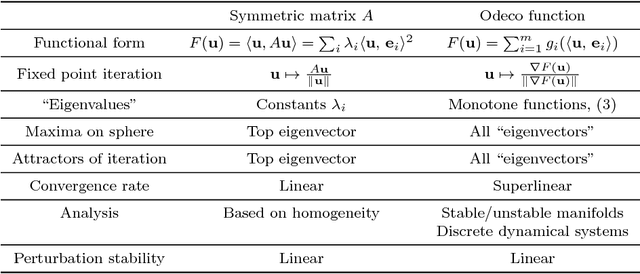
The Eigendecomposition of quadratic forms (symmetric matrices) guaranteed by the spectral theorem is a foundational result in applied mathematics. Motivated by a shared structure found in inferential problems of recent interest---namely orthogonal tensor decompositions, Independent Component Analysis (ICA), topic models, spectral clustering, and Gaussian mixture learning---we generalize the eigendecomposition from quadratic forms to a broad class of "orthogonally decomposable" functions. We identify a key role of convexity in our extension, and we generalize two traditional characterizations of eigenvectors: First, the eigenvectors of a quadratic form arise from the optima structure of the quadratic form on the sphere. Second, the eigenvectors are the fixed points of the power iteration. In our setting, we consider a simple first order generalization of the power method which we call gradient iteration. It leads to efficient and easily implementable methods for basis recovery. It includes influential Machine Learning methods such as cumulant-based FastICA and the tensor power iteration for orthogonally decomposable tensors as special cases. We provide a complete theoretical analysis of gradient iteration using the structure theory of discrete dynamical systems to show almost sure convergence and fast (super-linear) convergence rates. The analysis also extends to the case when the observed function is only approximately orthogonally decomposable, with bounds that are polynomial in dimension and other relevant parameters, such as perturbation size. Our perturbation results can be considered as a non-linear version of the classical Davis-Kahan theorem for perturbations of eigenvectors of symmetric matrices.

Heavy-Tailed Analogues of the Covariance Matrix for ICA

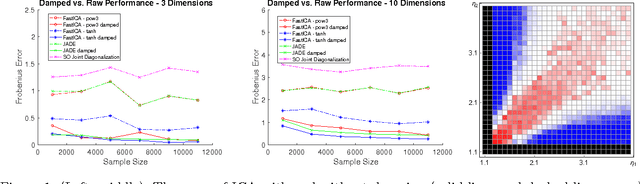
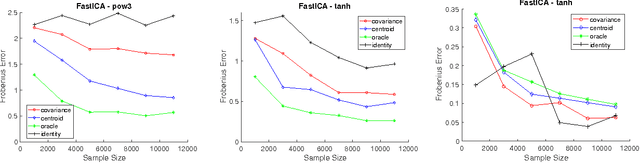
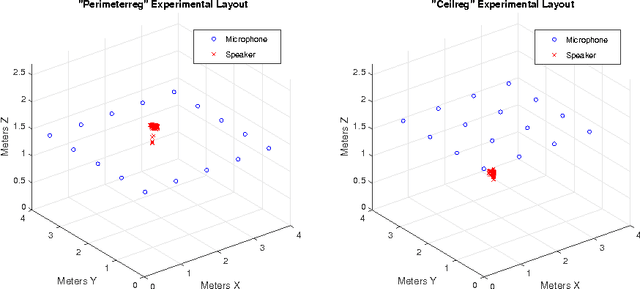
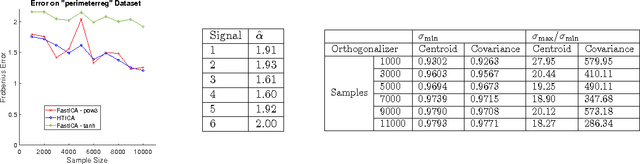
Independent Component Analysis (ICA) is the problem of learning a square matrix $A$, given samples of $X=AS$, where $S$ is a random vector with independent coordinates. Most existing algorithms are provably efficient only when each $S_i$ has finite and moderately valued fourth moment. However, there are practical applications where this assumption need not be true, such as speech and finance. Algorithms have been proposed for heavy-tailed ICA, but they are not practical, using random walks and the full power of the ellipsoid algorithm multiple times. The main contributions of this paper are: (1) A practical algorithm for heavy-tailed ICA that we call HTICA. We provide theoretical guarantees and show that it outperforms other algorithms in some heavy-tailed regimes, both on real and synthetic data. Like the current state-of-the-art, the new algorithm is based on the centroid body (a first moment analogue of the covariance matrix). Unlike the state-of-the-art, our algorithm is practically efficient. To achieve this, we use explicit analytic representations of the centroid body, which bypasses the use of the ellipsoid method and random walks. (2) We study how heavy tails affect different ICA algorithms, including HTICA. Somewhat surprisingly, we show that some algorithms that use the covariance matrix or higher moments can successfully solve a range of ICA instances with infinite second moment. We study this theoretically and experimentally, with both synthetic and real-world heavy-tailed data.

The Hidden Convexity of Spectral Clustering

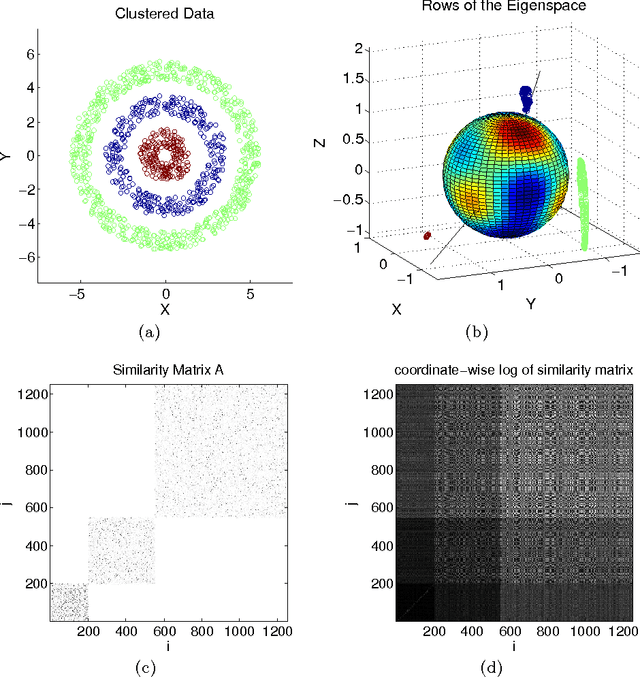
In recent years, spectral clustering has become a standard method for data analysis used in a broad range of applications. In this paper we propose a new class of algorithms for multiway spectral clustering based on optimization of a certain "contrast function" over the unit sphere. These algorithms, partly inspired by certain Independent Component Analysis techniques, are simple, easy to implement and efficient. Geometrically, the proposed algorithms can be interpreted as hidden basis recovery by means of function optimization. We give a complete characterization of the contrast functions admissible for provable basis recovery. We show how these conditions can be interpreted as a "hidden convexity" of our optimization problem on the sphere; interestingly, we use efficient convex maximization rather than the more common convex minimization. We also show encouraging experimental results on real and simulated data.

A Pseudo-Euclidean Iteration for Optimal Recovery in Noisy ICA

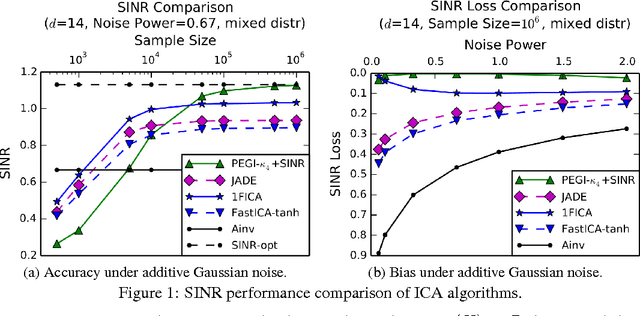
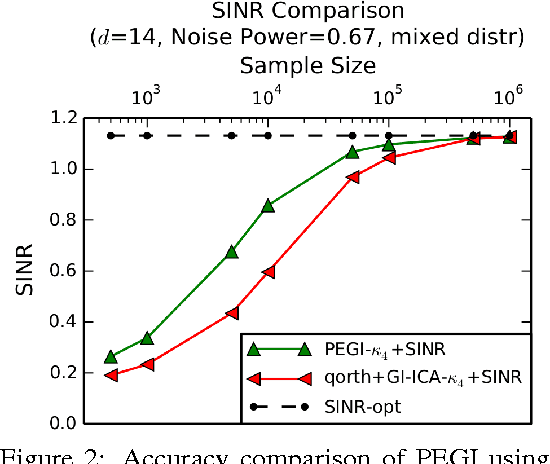
Independent Component Analysis (ICA) is a popular model for blind signal separation. The ICA model assumes that a number of independent source signals are linearly mixed to form the observed signals. We propose a new algorithm, PEGI (for pseudo-Euclidean Gradient Iteration), for provable model recovery for ICA with Gaussian noise. The main technical innovation of the algorithm is to use a fixed point iteration in a pseudo-Euclidean (indefinite "inner product") space. The use of this indefinite "inner product" resolves technical issues common to several existing algorithms for noisy ICA. This leads to an algorithm which is conceptually simple, efficient and accurate in testing. Our second contribution is combining PEGI with the analysis of objectives for optimal recovery in the noisy ICA model. It has been observed that the direct approach of demixing with the inverse of the mixing matrix is suboptimal for signal recovery in terms of the natural Signal to Interference plus Noise Ratio (SINR) criterion. There have been several partial solutions proposed in the ICA literature. It turns out that any solution to the mixing matrix reconstruction problem can be used to construct an SINR-optimal ICA demixing, despite the fact that SINR itself cannot be computed from data. That allows us to obtain a practical and provably SINR-optimal recovery method for ICA with arbitrary Gaussian noise.

Heavy-tailed Independent Component Analysis

Independent component analysis (ICA) is the problem of efficiently recovering a matrix $A \in \mathbb{R}^{n\times n}$ from i.i.d. observations of $X=AS$ where $S \in \mathbb{R}^n$ is a random vector with mutually independent coordinates. This problem has been intensively studied, but all existing efficient algorithms with provable guarantees require that the coordinates $S_i$ have finite fourth moments. We consider the heavy-tailed ICA problem where we do not make this assumption, about the second moment. This problem also has received considerable attention in the applied literature. In the present work, we first give a provably efficient algorithm that works under the assumption that for constant $\gamma > 0$, each $S_i$ has finite $(1+\gamma)$-moment, thus substantially weakening the moment requirement condition for the ICA problem to be solvable. We then give an algorithm that works under the assumption that matrix $A$ has orthogonal columns but requires no moment assumptions. Our techniques draw ideas from convex geometry and exploit standard properties of the multivariate spherical Gaussian distribution in a novel way.

The More, the Merrier: the Blessing of Dimensionality for Learning Large Gaussian Mixtures

In this paper we show that very large mixtures of Gaussians are efficiently learnable in high dimension. More precisely, we prove that a mixture with known identical covariance matrices whose number of components is a polynomial of any fixed degree in the dimension n is polynomially learnable as long as a certain non-degeneracy condition on the means is satisfied. It turns out that this condition is generic in the sense of smoothed complexity, as soon as the dimensionality of the space is high enough. Moreover, we prove that no such condition can possibly exist in low dimension and the problem of learning the parameters is generically hard. In contrast, much of the existing work on Gaussian Mixtures relies on low-dimensional projections and thus hits an artificial barrier. Our main result on mixture recovery relies on a new "Poissonization"-based technique, which transforms a mixture of Gaussians to a linear map of a product distribution. The problem of learning this map can be efficiently solved using some recent results on tensor decompositions and Independent Component Analysis (ICA), thus giving an algorithm for recovering the mixture. In addition, we combine our low-dimensional hardness results for Gaussian mixtures with Poissonization to show how to embed difficult instances of low-dimensional Gaussian mixtures into the ICA setting, thus establishing exponential information-theoretic lower bounds for underdetermined ICA in low dimension. To the best of our knowledge, this is the first such result in the literature. In addition to contributing to the problem of Gaussian mixture learning, we believe that this work is among the first steps toward better understanding the rare phenomenon of the "blessing of dimensionality" in the computational aspects of statistical inference.

Blind Signal Separation in the Presence of Gaussian Noise

A prototypical blind signal separation problem is the so-called cocktail party problem, with n people talking simultaneously and n different microphones within a room. The goal is to recover each speech signal from the microphone inputs. Mathematically this can be modeled by assuming that we are given samples from an n-dimensional random variable X=AS, where S is a vector whose coordinates are independent random variables corresponding to each speaker. The objective is to recover the matrix A^{-1} given random samples from X. A range of techniques collectively known as Independent Component Analysis (ICA) have been proposed to address this problem in the signal processing and machine learning literature. Many of these techniques are based on using the kurtosis or other cumulants to recover the components. In this paper we propose a new algorithm for solving the blind signal separation problem in the presence of additive Gaussian noise, when we are given samples from X=AS+\eta, where \eta is drawn from an unknown, not necessarily spherical n-dimensional Gaussian distribution. Our approach is based on a method for decorrelating a sample with additive Gaussian noise under the assumption that the underlying distribution is a linear transformation of a distribution with independent components. Our decorrelation routine is based on the properties of cumulant tensors and can be combined with any standard cumulant-based method for ICA to get an algorithm that is provably robust in the presence of Gaussian noise. We derive polynomial bounds for the sample complexity and error propagation of our method.

Efficient learning of simplices

We show an efficient algorithm for the following problem: Given uniformly random points from an arbitrary n-dimensional simplex, estimate the simplex. The size of the sample and the number of arithmetic operations of our algorithm are polynomial in n. This answers a question of Frieze, Jerrum and Kannan [FJK]. Our result can also be interpreted as efficiently learning the intersection of n+1 half-spaces in R^n in the model where the intersection is bounded and we are given polynomially many uniform samples from it. Our proof uses the local search technique from Independent Component Analysis (ICA), also used by [FJK]. Unlike these previous algorithms, which were based on analyzing the fourth moment, ours is based on the third moment. We also show a direct connection between the problem of learning a simplex and ICA: a simple randomized reduction to ICA from the problem of learning a simplex. The connection is based on a known representation of the uniform measure on a simplex. Similar representations lead to a reduction from the problem of learning an affine transformation of an n-dimensional l_p ball to ICA.