Non-Euclidean Differentially Private Stochastic Convex Optimization

Differentially private (DP) stochastic convex optimization (SCO) is a fundamental problem, where the goal is to approximately minimize the population risk with respect to a convex loss function, given a dataset of i.i.d. samples from a distribution, while satisfying differential privacy with respect to the dataset. Most of the existing works in the literature of private convex optimization focus on the Euclidean (i.e., $\ell_2$) setting, where the loss is assumed to be Lipschitz (and possibly smooth) w.r.t. the $\ell_2$ norm over a constraint set with bounded $\ell_2$ diameter. Algorithms based on noisy stochastic gradient descent (SGD) are known to attain the optimal excess risk in this setting. In this work, we conduct a systematic study of DP-SCO for $\ell_p$-setups. For $p=1$, under a standard smoothness assumption, we give a new algorithm with nearly optimal excess risk. This result also extends to general polyhedral norms and feasible sets. For $p\in(1, 2)$, we give two new algorithms, whose central building block is a novel privacy mechanism, which generalizes the Gaussian mechanism. Moreover, we establish a lower bound on the excess risk for this range of $p$, showing a necessary dependence on $\sqrt{d}$, where $d$ is the dimension of the space. Our lower bound implies a sudden transition of the excess risk at $p=1$, where the dependence on $d$ changes from logarithmic to polynomial, resolving an open question in prior work [TTZ15] . For $p\in (2, \infty)$, noisy SGD attains optimal excess risk in the low-dimensional regime; in particular, this proves the optimality of noisy SGD for $p=\infty$. Our work draws upon concepts from the geometry of normed spaces, such as the notions of regularity, uniform convexity, and uniform smoothness.

Learning from Mixtures of Private and Public Populations

We initiate the study of a new model of supervised learning under privacy constraints. Imagine a medical study where a dataset is sampled from a population of both healthy and unhealthy individuals. Suppose healthy individuals have no privacy concerns (in such case, we call their data "public") while the unhealthy individuals desire stringent privacy protection for their data. In this example, the population (data distribution) is a mixture of private (unhealthy) and public (healthy) sub-populations that could be very different. Inspired by the above example, we consider a model in which the population $\mathcal{D}$ is a mixture of two sub-populations: a private sub-population $\mathcal{D}_{\sf priv}$ of private and sensitive data, and a public sub-population $\mathcal{D}_{\sf pub}$ of data with no privacy concerns. Each example drawn from $\mathcal{D}$ is assumed to contain a privacy-status bit that indicates whether the example is private or public. The goal is to design a learning algorithm that satisfies differential privacy only with respect to the private examples. Prior works in this context assumed a homogeneous population where private and public data arise from the same distribution, and in particular designed solutions which exploit this assumption. We demonstrate how to circumvent this assumption by considering, as a case study, the problem of learning linear classifiers in $\mathbb{R}^d$. We show that in the case where the privacy status is correlated with the target label (as in the above example), linear classifiers in $\mathbb{R}^d$ can be learned, in the agnostic as well as the realizable setting, with sample complexity which is comparable to that of the classical (non-private) PAC-learning. It is known that this task is impossible if all the data is considered private.

Privately Answering Classification Queries in the Agnostic PAC Model

We revisit the problem of differentially private release of classification queries. In this problem, the goal is to design an algorithm that can accurately answer a sequence of classification queries based on a private training set while ensuring differential privacy. We formally study this problem in the agnostic PAC model and derive a new upper bound on the private sample complexity. Our results improve over those obtained in a recent work [BTT18] for the agnostic PAC setting. In particular, we give an improved construction that yields a tighter upper bound on the sample complexity. Moreover, unlike [BTT18], our accuracy guarantee does not involve any blow-up in the approximation error associated with the given hypothesis class. Given any hypothesis class with VC-dimension $d$, we show that our construction can privately answer up to $m$ classification queries with average excess error $\alpha$ using a private sample of size $\approx \frac{d}{\alpha^2}\max\left(1, \sqrt{m}\alpha^{3/2}\right)$. Using recent results on private learning with auxiliary public data, we extend our construction to show that one can privately answer any number of classification queries with average excess error $\alpha$ using a private sample of size $\approx \frac{d}{\alpha^2}\max\left(1, \sqrt{d} \alpha\right)$. Our results imply that when $\alpha$ is sufficiently small (high-accuracy regime), the private sample size is essentially the same as the non-private sample complexity of agnostic PAC learning.

Heavy-Tailed Analogues of the Covariance Matrix for ICA

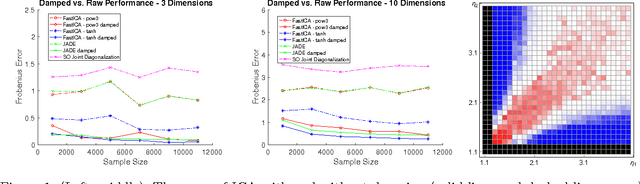
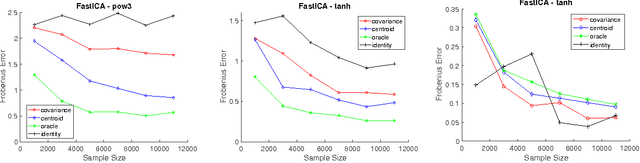
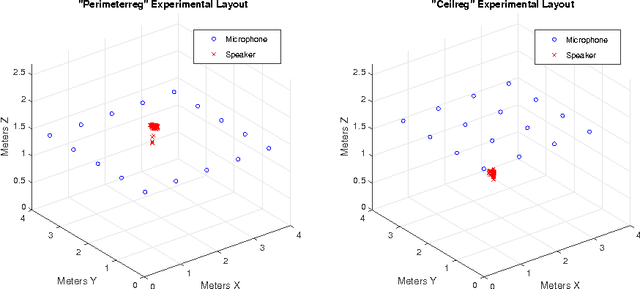
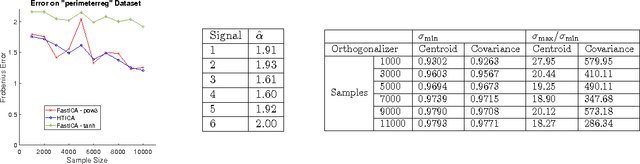
Independent Component Analysis (ICA) is the problem of learning a square matrix $A$, given samples of $X=AS$, where $S$ is a random vector with independent coordinates. Most existing algorithms are provably efficient only when each $S_i$ has finite and moderately valued fourth moment. However, there are practical applications where this assumption need not be true, such as speech and finance. Algorithms have been proposed for heavy-tailed ICA, but they are not practical, using random walks and the full power of the ellipsoid algorithm multiple times. The main contributions of this paper are: (1) A practical algorithm for heavy-tailed ICA that we call HTICA. We provide theoretical guarantees and show that it outperforms other algorithms in some heavy-tailed regimes, both on real and synthetic data. Like the current state-of-the-art, the new algorithm is based on the centroid body (a first moment analogue of the covariance matrix). Unlike the state-of-the-art, our algorithm is practically efficient. To achieve this, we use explicit analytic representations of the centroid body, which bypasses the use of the ellipsoid method and random walks. (2) We study how heavy tails affect different ICA algorithms, including HTICA. Somewhat surprisingly, we show that some algorithms that use the covariance matrix or higher moments can successfully solve a range of ICA instances with infinite second moment. We study this theoretically and experimentally, with both synthetic and real-world heavy-tailed data.

Heavy-tailed Independent Component Analysis

Independent component analysis (ICA) is the problem of efficiently recovering a matrix $A \in \mathbb{R}^{n\times n}$ from i.i.d. observations of $X=AS$ where $S \in \mathbb{R}^n$ is a random vector with mutually independent coordinates. This problem has been intensively studied, but all existing efficient algorithms with provable guarantees require that the coordinates $S_i$ have finite fourth moments. We consider the heavy-tailed ICA problem where we do not make this assumption, about the second moment. This problem also has received considerable attention in the applied literature. In the present work, we first give a provably efficient algorithm that works under the assumption that for constant $\gamma > 0$, each $S_i$ has finite $(1+\gamma)$-moment, thus substantially weakening the moment requirement condition for the ICA problem to be solvable. We then give an algorithm that works under the assumption that matrix $A$ has orthogonal columns but requires no moment assumptions. Our techniques draw ideas from convex geometry and exploit standard properties of the multivariate spherical Gaussian distribution in a novel way.