Improving Colorectal Cancer Screening and Risk Assessment through Predictive Modeling on Medical Images and Records

Colonoscopy screening is an effective method to find and remove colon polyps before they can develop into colorectal cancer (CRC). Current follow-up recommendations, as outlined by the U.S. Multi-Society Task Force for individuals found to have polyps, primarily rely on histopathological characteristics, neglecting other significant CRC risk factors. Moreover, the considerable variability in colorectal polyp characterization among pathologists poses challenges in effective colonoscopy follow-up or surveillance. The evolution of digital pathology and recent advancements in deep learning provide a unique opportunity to investigate the added benefits of including the additional medical record information and automatic processing of pathology slides using computer vision techniques in the calculation of future CRC risk. Leveraging the New Hampshire Colonoscopy Registry's extensive dataset, many with longitudinal colonoscopy follow-up information, we adapted our recently developed transformer-based model for histopathology image analysis in 5-year CRC risk prediction. Additionally, we investigated various multimodal fusion techniques, combining medical record information with deep learning derived risk estimates. Our findings reveal that training a transformer model to predict intermediate clinical variables contributes to enhancing 5-year CRC risk prediction performance, with an AUC of 0.630 comparing to direct prediction. Furthermore, the fusion of imaging and non-imaging features, while not requiring manual inspection of microscopy images, demonstrates improved predictive capabilities for 5-year CRC risk comparing to variables extracted from colonoscopy procedure and microscopy findings. This study signifies the potential of integrating diverse data sources and advanced computational techniques in transforming the accuracy and effectiveness of future CRC risk assessments.

Geometric Methods for Robust Data Analysis in High Dimension

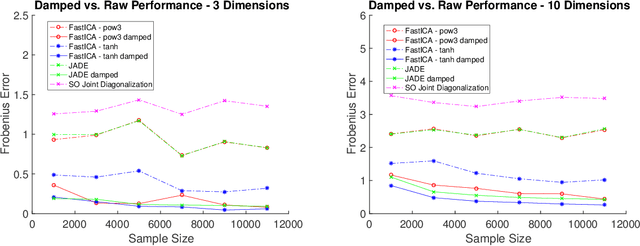
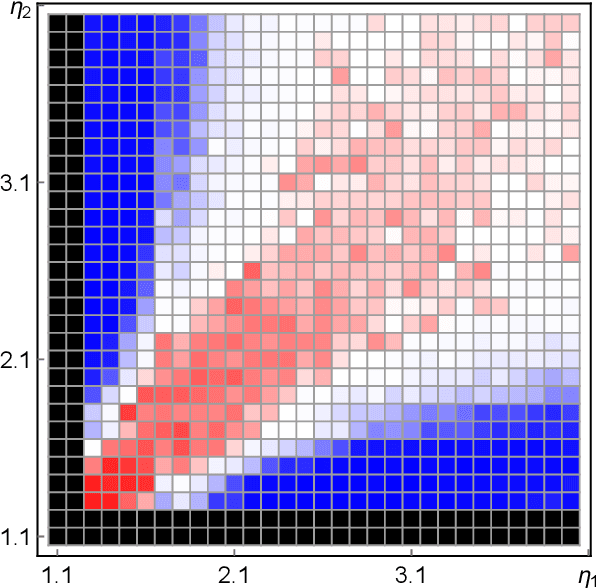
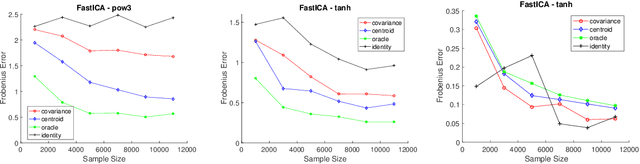
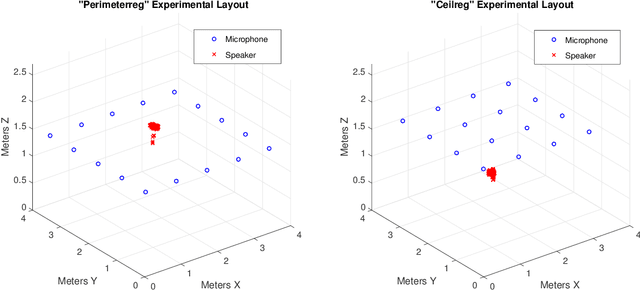
Machine learning and data analysis now finds both scientific and industrial application in biology, chemistry, geology, medicine, and physics. These applications rely on large quantities of data gathered from automated sensors and user input. Furthermore, the dimensionality of many datasets is extreme: more details are being gathered about single user interactions or sensor readings. All of these applications encounter problems with a common theme: use observed data to make inferences about the world. Our work obtains the first provably efficient algorithms for Independent Component Analysis (ICA) in the presence of heavy-tailed data. The main tool in this result is the centroid body (a well-known topic in convex geometry), along with optimization and random walks for sampling from a convex body. This is the first algorithmic use of the centroid body and it is of independent theoretical interest, since it effectively replaces the estimation of covariance from samples, and is more generally accessible. This reduction relies on a non-linear transformation of samples from such an intersection of halfspaces (i.e. a simplex) to samples which are approximately from a linearly transformed product distribution. Through this transformation of samples, which can be done efficiently, one can then use an ICA algorithm to recover the vertices of the intersection of halfspaces. Finally, we again use ICA as an algorithmic primitive to construct an efficient solution to the widely-studied problem of learning the parameters of a Gaussian mixture model. Our algorithm again transforms samples from a Gaussian mixture model into samples which fit into the ICA model and, when processed by an ICA algorithm, result in recovery of the mixture parameters. Our algorithm is effective even when the number of Gaussians in the mixture grows polynomially with the ambient dimension

Heavy-Tailed Analogues of the Covariance Matrix for ICA

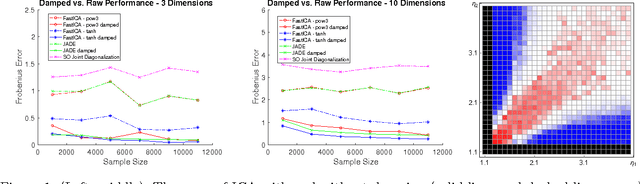
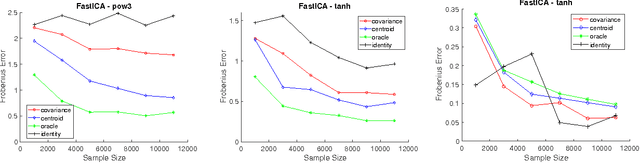
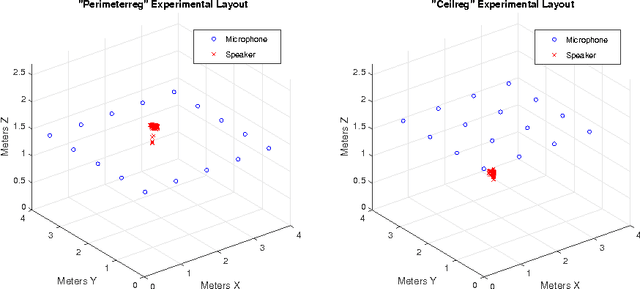
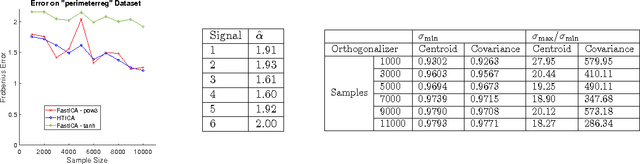
Independent Component Analysis (ICA) is the problem of learning a square matrix $A$, given samples of $X=AS$, where $S$ is a random vector with independent coordinates. Most existing algorithms are provably efficient only when each $S_i$ has finite and moderately valued fourth moment. However, there are practical applications where this assumption need not be true, such as speech and finance. Algorithms have been proposed for heavy-tailed ICA, but they are not practical, using random walks and the full power of the ellipsoid algorithm multiple times. The main contributions of this paper are: (1) A practical algorithm for heavy-tailed ICA that we call HTICA. We provide theoretical guarantees and show that it outperforms other algorithms in some heavy-tailed regimes, both on real and synthetic data. Like the current state-of-the-art, the new algorithm is based on the centroid body (a first moment analogue of the covariance matrix). Unlike the state-of-the-art, our algorithm is practically efficient. To achieve this, we use explicit analytic representations of the centroid body, which bypasses the use of the ellipsoid method and random walks. (2) We study how heavy tails affect different ICA algorithms, including HTICA. Somewhat surprisingly, we show that some algorithms that use the covariance matrix or higher moments can successfully solve a range of ICA instances with infinite second moment. We study this theoretically and experimentally, with both synthetic and real-world heavy-tailed data.

Heavy-tailed Independent Component Analysis

Independent component analysis (ICA) is the problem of efficiently recovering a matrix $A \in \mathbb{R}^{n\times n}$ from i.i.d. observations of $X=AS$ where $S \in \mathbb{R}^n$ is a random vector with mutually independent coordinates. This problem has been intensively studied, but all existing efficient algorithms with provable guarantees require that the coordinates $S_i$ have finite fourth moments. We consider the heavy-tailed ICA problem where we do not make this assumption, about the second moment. This problem also has received considerable attention in the applied literature. In the present work, we first give a provably efficient algorithm that works under the assumption that for constant $\gamma > 0$, each $S_i$ has finite $(1+\gamma)$-moment, thus substantially weakening the moment requirement condition for the ICA problem to be solvable. We then give an algorithm that works under the assumption that matrix $A$ has orthogonal columns but requires no moment assumptions. Our techniques draw ideas from convex geometry and exploit standard properties of the multivariate spherical Gaussian distribution in a novel way.

The More, the Merrier: the Blessing of Dimensionality for Learning Large Gaussian Mixtures

In this paper we show that very large mixtures of Gaussians are efficiently learnable in high dimension. More precisely, we prove that a mixture with known identical covariance matrices whose number of components is a polynomial of any fixed degree in the dimension n is polynomially learnable as long as a certain non-degeneracy condition on the means is satisfied. It turns out that this condition is generic in the sense of smoothed complexity, as soon as the dimensionality of the space is high enough. Moreover, we prove that no such condition can possibly exist in low dimension and the problem of learning the parameters is generically hard. In contrast, much of the existing work on Gaussian Mixtures relies on low-dimensional projections and thus hits an artificial barrier. Our main result on mixture recovery relies on a new "Poissonization"-based technique, which transforms a mixture of Gaussians to a linear map of a product distribution. The problem of learning this map can be efficiently solved using some recent results on tensor decompositions and Independent Component Analysis (ICA), thus giving an algorithm for recovering the mixture. In addition, we combine our low-dimensional hardness results for Gaussian mixtures with Poissonization to show how to embed difficult instances of low-dimensional Gaussian mixtures into the ICA setting, thus establishing exponential information-theoretic lower bounds for underdetermined ICA in low dimension. To the best of our knowledge, this is the first such result in the literature. In addition to contributing to the problem of Gaussian mixture learning, we believe that this work is among the first steps toward better understanding the rare phenomenon of the "blessing of dimensionality" in the computational aspects of statistical inference.

Efficient learning of simplices

We show an efficient algorithm for the following problem: Given uniformly random points from an arbitrary n-dimensional simplex, estimate the simplex. The size of the sample and the number of arithmetic operations of our algorithm are polynomial in n. This answers a question of Frieze, Jerrum and Kannan [FJK]. Our result can also be interpreted as efficiently learning the intersection of n+1 half-spaces in R^n in the model where the intersection is bounded and we are given polynomially many uniform samples from it. Our proof uses the local search technique from Independent Component Analysis (ICA), also used by [FJK]. Unlike these previous algorithms, which were based on analyzing the fourth moment, ours is based on the third moment. We also show a direct connection between the problem of learning a simplex and ICA: a simple randomized reduction to ICA from the problem of learning a simplex. The connection is based on a known representation of the uniform measure on a simplex. Similar representations lead to a reduction from the problem of learning an affine transformation of an n-dimensional l_p ball to ICA.