Eigenvectors of Orthogonally Decomposable Functions

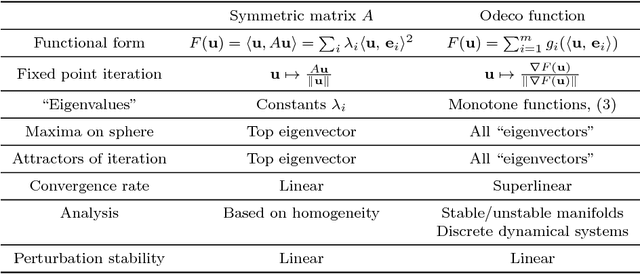
The Eigendecomposition of quadratic forms (symmetric matrices) guaranteed by the spectral theorem is a foundational result in applied mathematics. Motivated by a shared structure found in inferential problems of recent interest---namely orthogonal tensor decompositions, Independent Component Analysis (ICA), topic models, spectral clustering, and Gaussian mixture learning---we generalize the eigendecomposition from quadratic forms to a broad class of "orthogonally decomposable" functions. We identify a key role of convexity in our extension, and we generalize two traditional characterizations of eigenvectors: First, the eigenvectors of a quadratic form arise from the optima structure of the quadratic form on the sphere. Second, the eigenvectors are the fixed points of the power iteration. In our setting, we consider a simple first order generalization of the power method which we call gradient iteration. It leads to efficient and easily implementable methods for basis recovery. It includes influential Machine Learning methods such as cumulant-based FastICA and the tensor power iteration for orthogonally decomposable tensors as special cases. We provide a complete theoretical analysis of gradient iteration using the structure theory of discrete dynamical systems to show almost sure convergence and fast (super-linear) convergence rates. The analysis also extends to the case when the observed function is only approximately orthogonally decomposable, with bounds that are polynomial in dimension and other relevant parameters, such as perturbation size. Our perturbation results can be considered as a non-linear version of the classical Davis-Kahan theorem for perturbations of eigenvectors of symmetric matrices.