A Scalable Framework for Evaluating Health Language Models

Large language models (LLMs) have emerged as powerful tools for analyzing complex datasets. Recent studies demonstrate their potential to generate useful, personalized responses when provided with patient-specific health information that encompasses lifestyle, biomarkers, and context. As LLM-driven health applications are increasingly adopted, rigorous and efficient one-sided evaluation methodologies are crucial to ensure response quality across multiple dimensions, including accuracy, personalization and safety. Current evaluation practices for open-ended text responses heavily rely on human experts. This approach introduces human factors and is often cost-prohibitive, labor-intensive, and hinders scalability, especially in complex domains like healthcare where response assessment necessitates domain expertise and considers multifaceted patient data. In this work, we introduce Adaptive Precise Boolean rubrics: an evaluation framework that streamlines human and automated evaluation of open-ended questions by identifying gaps in model responses using a minimal set of targeted rubrics questions. Our approach is based on recent work in more general evaluation settings that contrasts a smaller set of complex evaluation targets with a larger set of more precise, granular targets answerable with simple boolean responses. We validate this approach in metabolic health, a domain encompassing diabetes, cardiovascular disease, and obesity. Our results demonstrate that Adaptive Precise Boolean rubrics yield higher inter-rater agreement among expert and non-expert human evaluators, and in automated assessments, compared to traditional Likert scales, while requiring approximately half the evaluation time of Likert-based methods. This enhanced efficiency, particularly in automated evaluation and non-expert contributions, paves the way for more extensive and cost-effective evaluation of LLMs in health.

Emergence in non-neural models: grokking modular arithmetic via average gradient outer product

Neural networks trained to solve modular arithmetic tasks exhibit grokking, a phenomenon where the test accuracy starts improving long after the model achieves 100% training accuracy in the training process. It is often taken as an example of "emergence", where model ability manifests sharply through a phase transition. In this work, we show that the phenomenon of grokking is not specific to neural networks nor to gradient descent-based optimization. Specifically, we show that this phenomenon occurs when learning modular arithmetic with Recursive Feature Machines (RFM), an iterative algorithm that uses the Average Gradient Outer Product (AGOP) to enable task-specific feature learning with general machine learning models. When used in conjunction with kernel machines, iterating RFM results in a fast transition from random, near zero, test accuracy to perfect test accuracy. This transition cannot be predicted from the training loss, which is identically zero, nor from the test loss, which remains constant in initial iterations. Instead, as we show, the transition is completely determined by feature learning: RFM gradually learns block-circulant features to solve modular arithmetic. Paralleling the results for RFM, we show that neural networks that solve modular arithmetic also learn block-circulant features. Furthermore, we present theoretical evidence that RFM uses such block-circulant features to implement the Fourier Multiplication Algorithm, which prior work posited as the generalizing solution neural networks learn on these tasks. Our results demonstrate that emergence can result purely from learning task-relevant features and is not specific to neural architectures nor gradient descent-based optimization methods. Furthermore, our work provides more evidence for AGOP as a key mechanism for feature learning in neural networks.

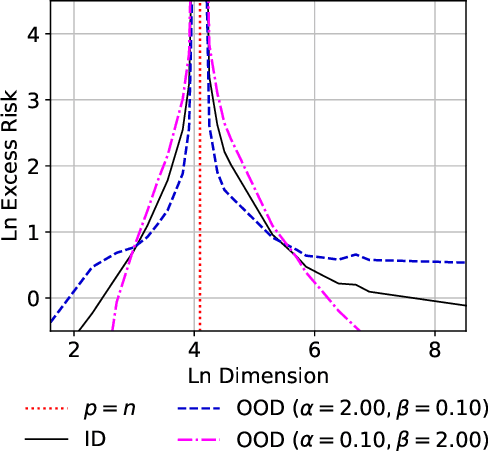
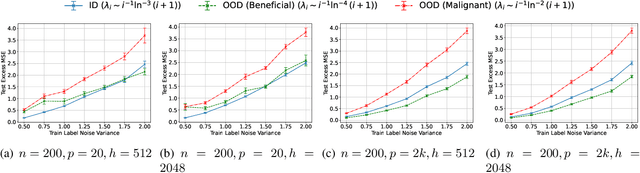
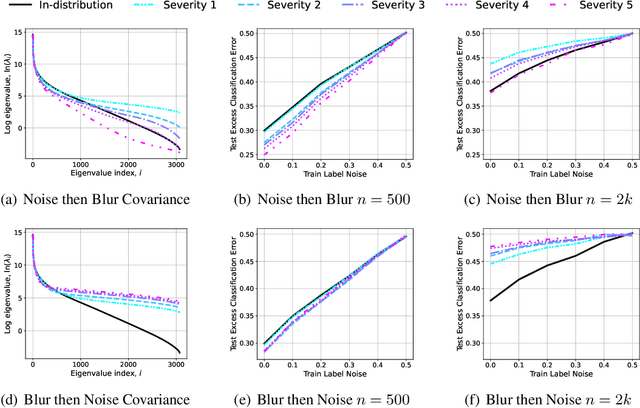
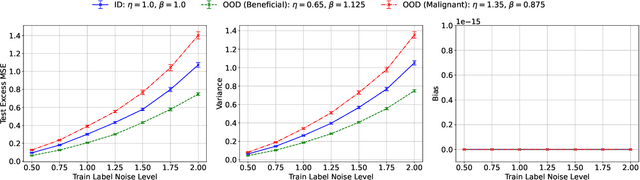
Minimum-Norm Interpolation Under Covariate Shift

Transfer learning is a critical part of real-world machine learning deployments and has been extensively studied in experimental works with overparameterized neural networks. However, even in the simplest setting of linear regression a notable gap still exists in the theoretical understanding of transfer learning. In-distribution research on high-dimensional linear regression has led to the identification of a phenomenon known as \textit{benign overfitting}, in which linear interpolators overfit to noisy training labels and yet still generalize well. This behavior occurs under specific conditions on the source covariance matrix and input data dimension. Therefore, it is natural to wonder how such high-dimensional linear models behave under transfer learning. We prove the first non-asymptotic excess risk bounds for benignly-overfit linear interpolators in the transfer learning setting. From our analysis, we propose a taxonomy of \textit{beneficial} and \textit{malignant} covariate shifts based on the degree of overparameterization. We follow our analysis with empirical studies that show these beneficial and malignant covariate shifts for linear interpolators on real image data, and for fully-connected neural networks in settings where the input data dimension is larger than the training sample size.

The Calibration Generalization Gap

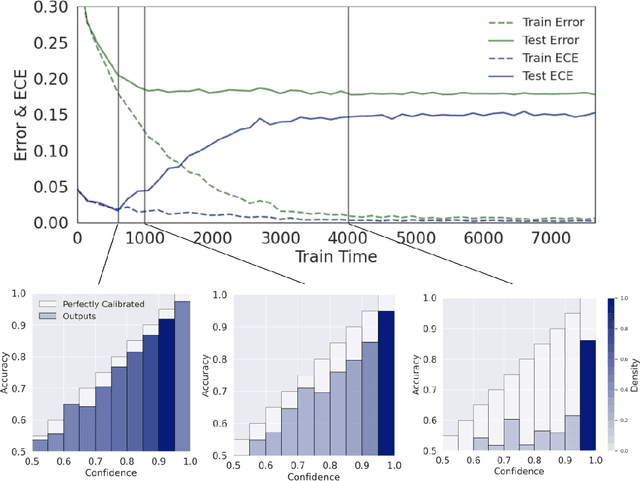
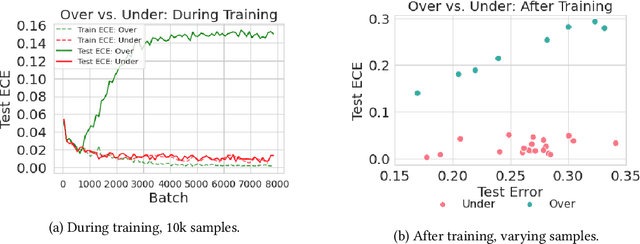
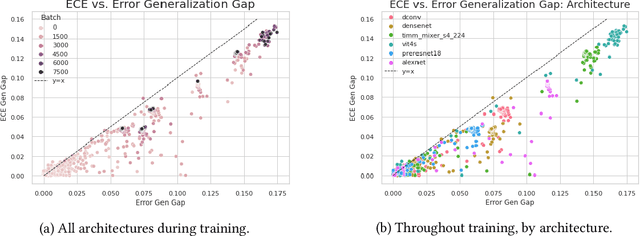
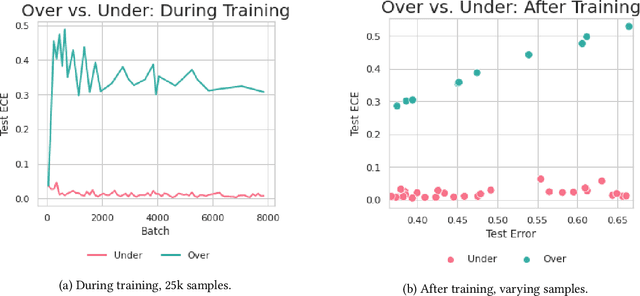
Calibration is a fundamental property of a good predictive model: it requires that the model predicts correctly in proportion to its confidence. Modern neural networks, however, provide no strong guarantees on their calibration -- and can be either poorly calibrated or well-calibrated depending on the setting. It is currently unclear which factors contribute to good calibration (architecture, data augmentation, overparameterization, etc), though various claims exist in the literature. We propose a systematic way to study the calibration error: by decomposing it into (1) calibration error on the train set, and (2) the calibration generalization gap. This mirrors the fundamental decomposition of generalization. We then investigate each of these terms, and give empirical evidence that (1) DNNs are typically always calibrated on their train set, and (2) the calibration generalization gap is upper-bounded by the standard generalization gap. Taken together, this implies that models with small generalization gap (|Test Error - Train Error|) are well-calibrated. This perspective unifies many results in the literature, and suggests that interventions which reduce the generalization gap (such as adding data, using heavy augmentation, or smaller model size) also improve calibration. We thus hope our initial study lays the groundwork for a more systematic and comprehensive understanding of the relation between calibration, generalization, and optimization.

Benign, Tempered, or Catastrophic: A Taxonomy of Overfitting

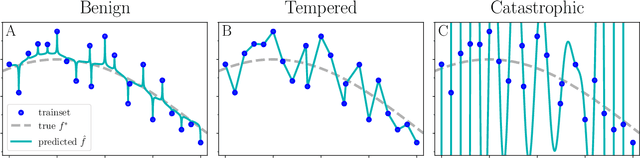
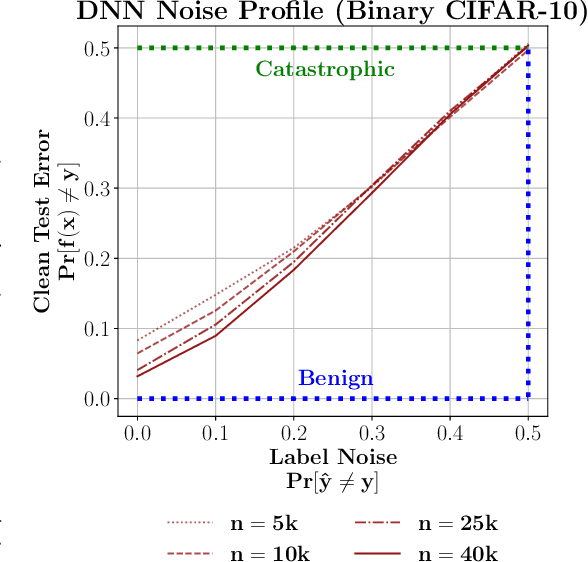
The practical success of overparameterized neural networks has motivated the recent scientific study of interpolating methods, which perfectly fit their training data. Certain interpolating methods, including neural networks, can fit noisy training data without catastrophically bad test performance, in defiance of standard intuitions from statistical learning theory. Aiming to explain this, a body of recent work has studied $\textit{benign overfitting}$, a phenomenon where some interpolating methods approach Bayes optimality, even in the presence of noise. In this work we argue that while benign overfitting has been instructive and fruitful to study, many real interpolating methods like neural networks $\textit{do not fit benignly}$: modest noise in the training set causes nonzero (but non-infinite) excess risk at test time, implying these models are neither benign nor catastrophic but rather fall in an intermediate regime. We call this intermediate regime $\textit{tempered overfitting}$, and we initiate its systematic study. We first explore this phenomenon in the context of kernel (ridge) regression (KR) by obtaining conditions on the ridge parameter and kernel eigenspectrum under which KR exhibits each of the three behaviors. We find that kernels with powerlaw spectra, including Laplace kernels and ReLU neural tangent kernels, exhibit tempered overfitting. We then empirically study deep neural networks through the lens of our taxonomy, and find that those trained to interpolation are tempered, while those stopped early are benign. We hope our work leads to a more refined understanding of overfitting in modern learning.

Iterative Data Programming for Expanding Text Classification Corpora

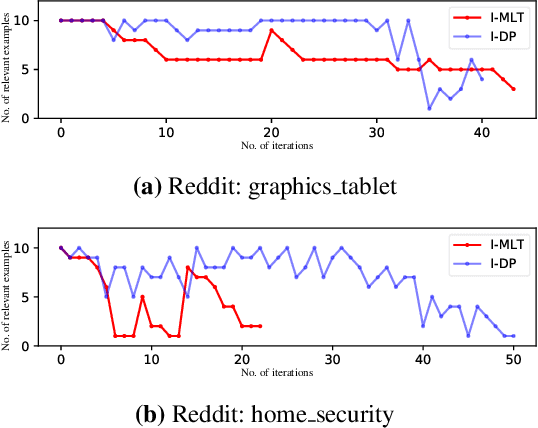
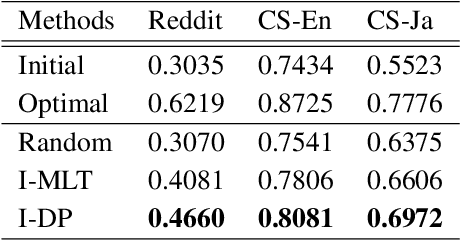
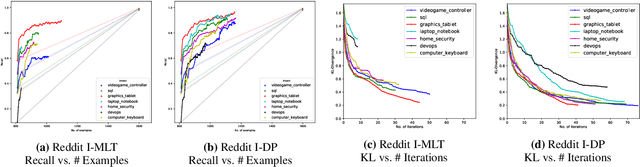
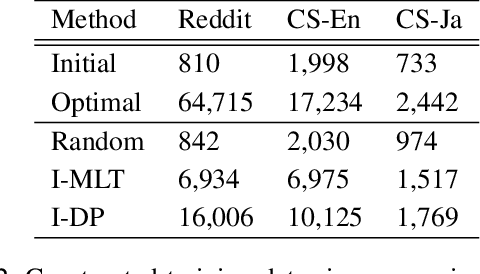
Real-world text classification tasks often require many labeled training examples that are expensive to obtain. Recent advancements in machine teaching, specifically the data programming paradigm, facilitate the creation of training data sets quickly via a general framework for building weak models, also known as labeling functions, and denoising them through ensemble learning techniques. We present a fast, simple data programming method for augmenting text data sets by generating neighborhood-based weak models with minimal supervision. Furthermore, our method employs an iterative procedure to identify sparsely distributed examples from large volumes of unlabeled data. The iterative data programming techniques improve newer weak models as more labeled data is confirmed with human-in-loop. We show empirical results on sentence classification tasks, including those from a task of improving intent recognition in conversational agents.

Multi-Frame Cross-Entropy Training for Convolutional Neural Networks in Speech Recognition

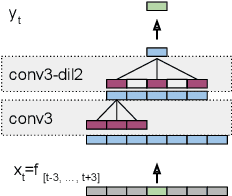
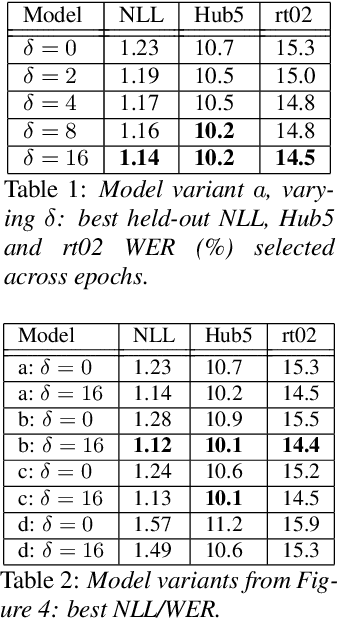
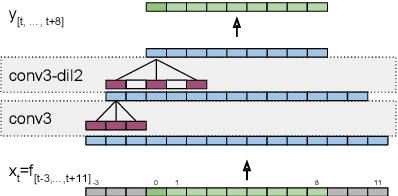
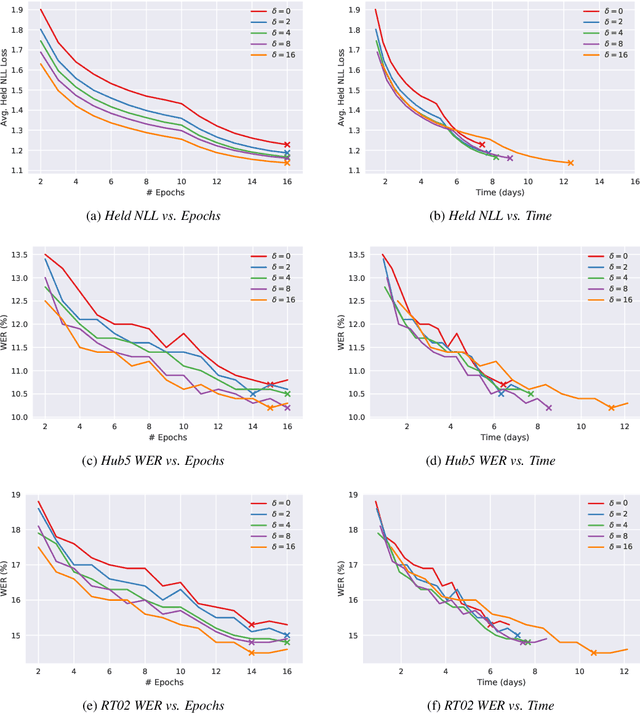
We introduce Multi-Frame Cross-Entropy training (MFCE) for convolutional neural network acoustic models. Recognizing that similar to RNNs, CNNs are in nature sequence models that take variable length inputs, we propose to take as input to the CNN a part of an utterance long enough that multiple labels are predicted at once, therefore getting cross-entropy loss signal from multiple adjacent frames. This increases the amount of label information drastically for small marginal computational cost. We show large WER improvements on hub5 and rt02 after training on the 2000-hour Switchboard benchmark.

Bootstrapping Conversational Agents With Weak Supervision

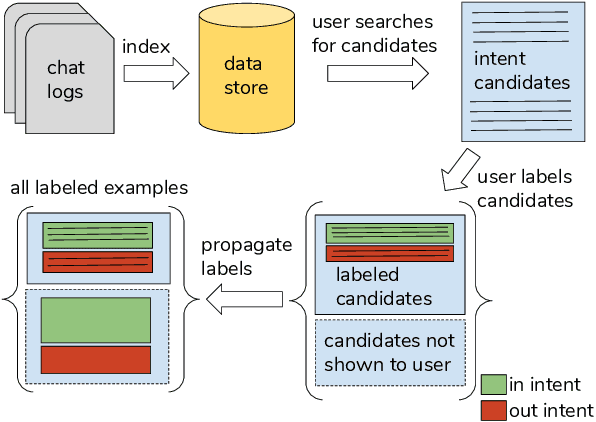
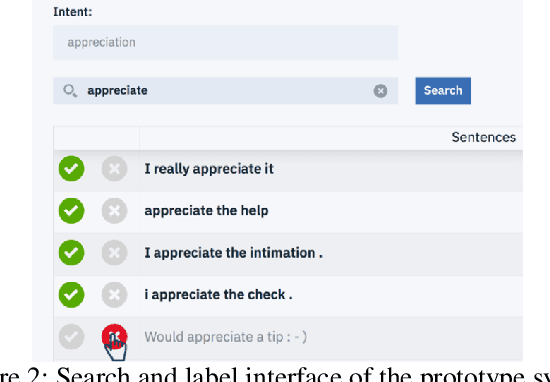
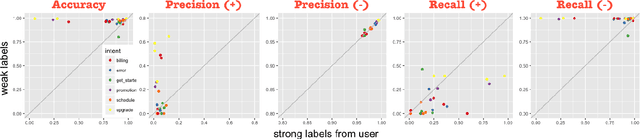
Many conversational agents in the market today follow a standard bot development framework which requires training intent classifiers to recognize user input. The need to create a proper set of training examples is often the bottleneck in the development process. In many occasions agent developers have access to historical chat logs that can provide a good quantity as well as coverage of training examples. However, the cost of labeling them with tens to hundreds of intents often prohibits taking full advantage of these chat logs. In this paper, we present a framework called \textit{search, label, and propagate} (SLP) for bootstrapping intents from existing chat logs using weak supervision. The framework reduces hours to days of labeling effort down to minutes of work by using a search engine to find examples, then relies on a data programming approach to automatically expand the labels. We report on a user study that shows positive user feedback for this new approach to build conversational agents, and demonstrates the effectiveness of using data programming for auto-labeling. While the system is developed for training conversational agents, the framework has broader application in significantly reducing labeling effort for training text classifiers.

Big-Little Net: An Efficient Multi-Scale Feature Representation for Visual and Speech Recognition

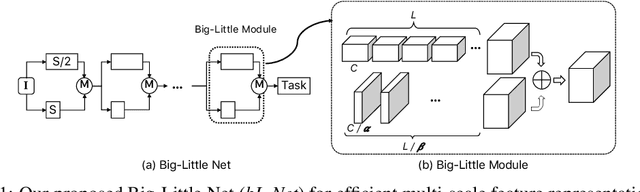
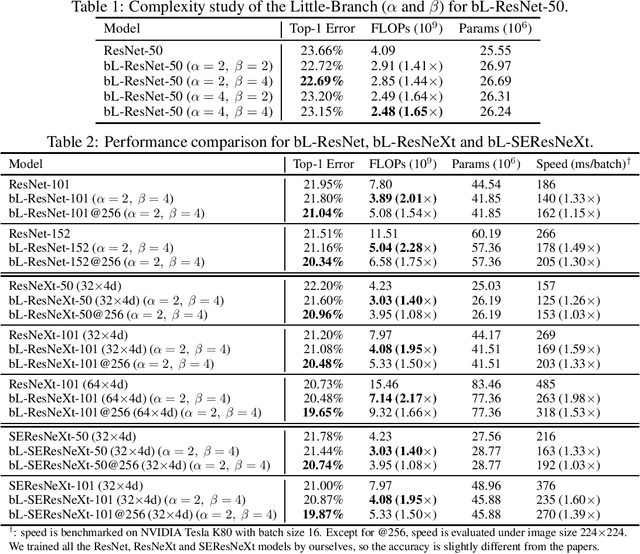
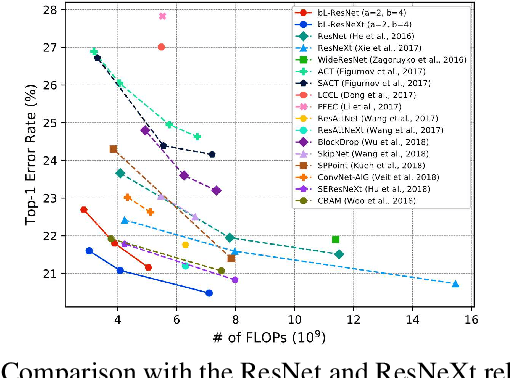
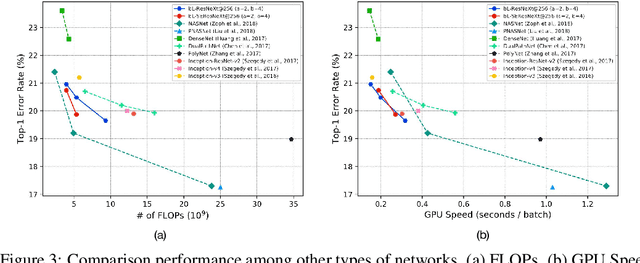
In this paper, we propose a novel Convolutional Neural Network (CNN) architecture for learning multi-scale feature representations with good tradeoffs between speed and accuracy. This is achieved by using a multi-branch network, which has different computational complexity at different branches. Through frequent merging of features from branches at distinct scales, our model obtains multi-scale features while using less computation. The proposed approach demonstrates improvement of model efficiency and performance on both object recognition and speech recognition tasks,using popular architectures including ResNet and ResNeXt. For object recognition, our approach reduces computation by 33% on object recognition while improving accuracy with 0.9%. Furthermore, our model surpasses state-of-the-art CNN acceleration approaches by a large margin in accuracy and FLOPs reduction. On the task of speech recognition, our proposed multi-scale CNNs save 30% FLOPs with slightly better word error rates, showing good generalization across domains.

Deep Canonically Correlated LSTMs

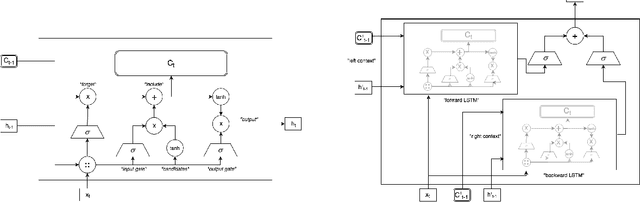
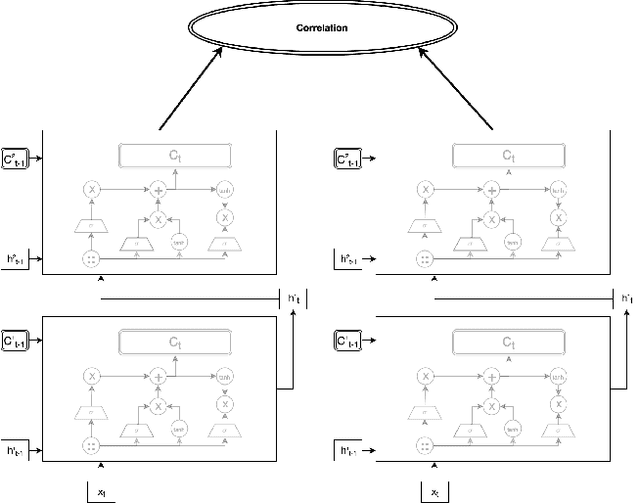
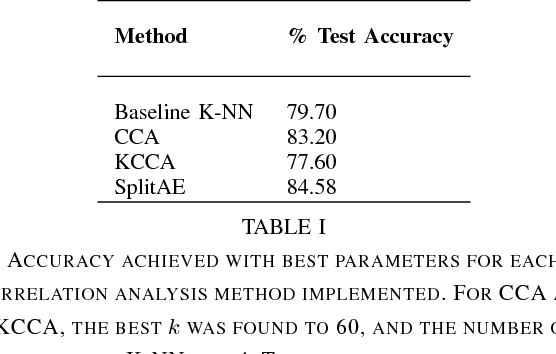
We examine Deep Canonically Correlated LSTMs as a way to learn nonlinear transformations of variable length sequences and embed them into a correlated, fixed dimensional space. We use LSTMs to transform multi-view time-series data non-linearly while learning temporal relationships within the data. We then perform correlation analysis on the outputs of these neural networks to find a correlated subspace through which we get our final representation via projection. This work follows from previous work done on Deep Canonical Correlation (DCCA), in which deep feed-forward neural networks were used to learn nonlinear transformations of data while maximizing correlation.