Benign, Tempered, or Catastrophic: A Taxonomy of Overfitting

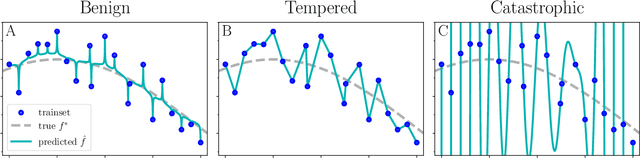
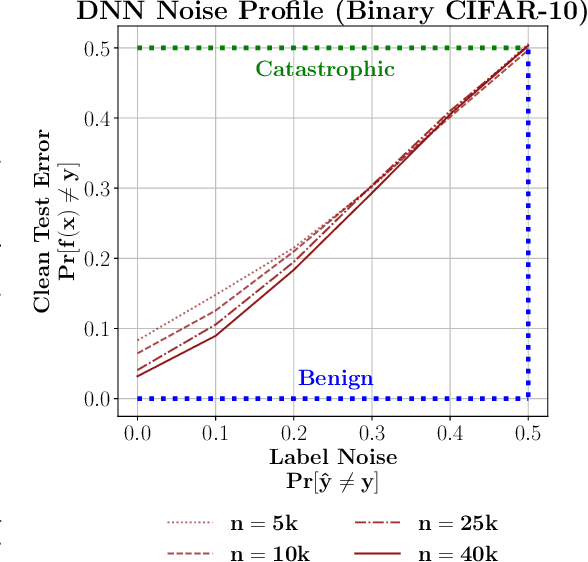
The practical success of overparameterized neural networks has motivated the recent scientific study of interpolating methods, which perfectly fit their training data. Certain interpolating methods, including neural networks, can fit noisy training data without catastrophically bad test performance, in defiance of standard intuitions from statistical learning theory. Aiming to explain this, a body of recent work has studied $\textit{benign overfitting}$, a phenomenon where some interpolating methods approach Bayes optimality, even in the presence of noise. In this work we argue that while benign overfitting has been instructive and fruitful to study, many real interpolating methods like neural networks $\textit{do not fit benignly}$: modest noise in the training set causes nonzero (but non-infinite) excess risk at test time, implying these models are neither benign nor catastrophic but rather fall in an intermediate regime. We call this intermediate regime $\textit{tempered overfitting}$, and we initiate its systematic study. We first explore this phenomenon in the context of kernel (ridge) regression (KR) by obtaining conditions on the ridge parameter and kernel eigenspectrum under which KR exhibits each of the three behaviors. We find that kernels with powerlaw spectra, including Laplace kernels and ReLU neural tangent kernels, exhibit tempered overfitting. We then empirically study deep neural networks through the lens of our taxonomy, and find that those trained to interpolation are tempered, while those stopped early are benign. We hope our work leads to a more refined understanding of overfitting in modern learning.