Adversarial Robustness of In-Context Learning in Transformers for Linear Regression

Transformers have demonstrated remarkable in-context learning capabilities across various domains, including statistical learning tasks. While previous work has shown that transformers can implement common learning algorithms, the adversarial robustness of these learned algorithms remains unexplored. This work investigates the vulnerability of in-context learning in transformers to \textit{hijacking attacks} focusing on the setting of linear regression tasks. Hijacking attacks are prompt-manipulation attacks in which the adversary's goal is to manipulate the prompt to force the transformer to generate a specific output. We first prove that single-layer linear transformers, known to implement gradient descent in-context, are non-robust and can be manipulated to output arbitrary predictions by perturbing a single example in the in-context training set. While our experiments show these attacks succeed on linear transformers, we find they do not transfer to more complex transformers with GPT-2 architectures. Nonetheless, we show that these transformers can be hijacked using gradient-based adversarial attacks. We then demonstrate that adversarial training enhances transformers' robustness against hijacking attacks, even when just applied during finetuning. Additionally, we find that in some settings, adversarial training against a weaker attack model can lead to robustness to a stronger attack model. Lastly, we investigate the transferability of hijacking attacks across transformers of varying scales and initialization seeds, as well as between transformers and ordinary least squares (OLS). We find that while attacks transfer effectively between small-scale transformers, they show poor transferability in other scenarios (small-to-large scale, large-to-large scale, and between transformers and OLS).

Benign Overfitting in Single-Head Attention

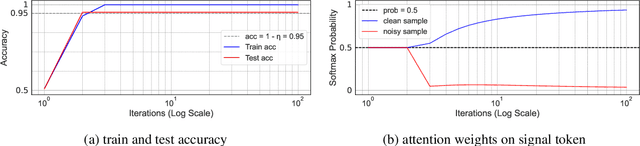
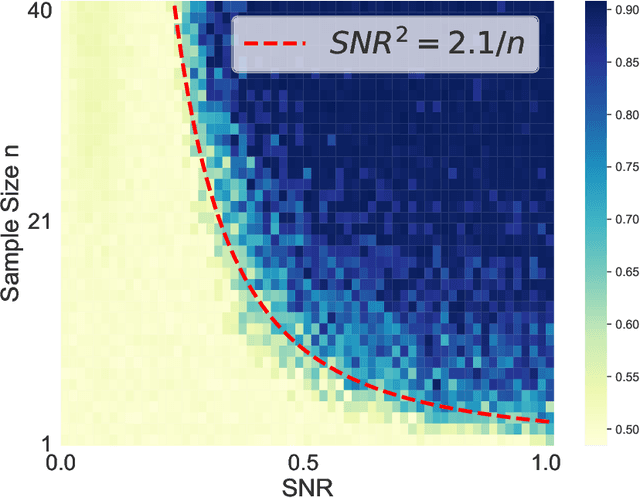
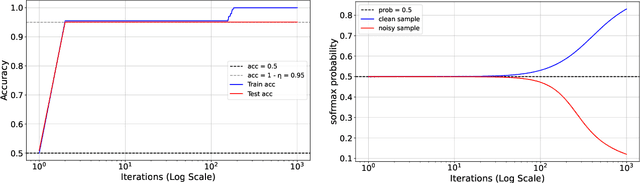
The phenomenon of benign overfitting, where a trained neural network perfectly fits noisy training data but still achieves near-optimal test performance, has been extensively studied in recent years for linear models and fully-connected/convolutional networks. In this work, we study benign overfitting in a single-head softmax attention model, which is the fundamental building block of Transformers. We prove that under appropriate conditions, the model exhibits benign overfitting in a classification setting already after two steps of gradient descent. Moreover, we show conditions where a minimum-norm/maximum-margin interpolator exhibits benign overfitting. We study how the overfitting behavior depends on the signal-to-noise ratio (SNR) of the data distribution, namely, the ratio between norms of signal and noise tokens, and prove that a sufficiently large SNR is both necessary and sufficient for benign overfitting.

Trained Transformer Classifiers Generalize and Exhibit Benign Overfitting In-Context

Transformers have the capacity to act as supervised learning algorithms: by properly encoding a set of labeled training ("in-context") examples and an unlabeled test example into an input sequence of vectors of the same dimension, the forward pass of the transformer can produce predictions for that unlabeled test example. A line of recent work has shown that when linear transformers are pre-trained on random instances for linear regression tasks, these trained transformers make predictions using an algorithm similar to that of ordinary least squares. In this work, we investigate the behavior of linear transformers trained on random linear classification tasks. Via an analysis of the implicit regularization of gradient descent, we characterize how many pre-training tasks and in-context examples are needed for the trained transformer to generalize well at test-time. We further show that in some settings, these trained transformers can exhibit "benign overfitting in-context": when in-context examples are corrupted by label flipping noise, the transformer memorizes all of its in-context examples (including those with noisy labels) yet still generalizes near-optimally for clean test examples.

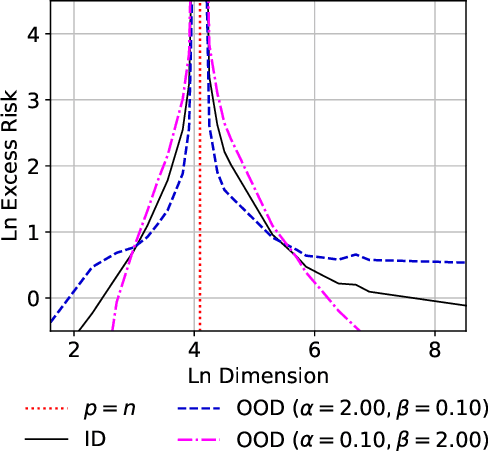
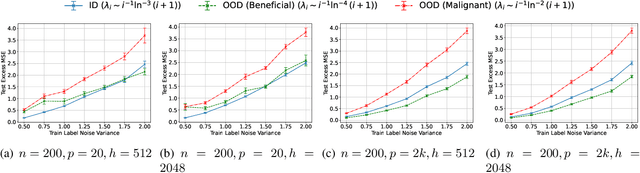
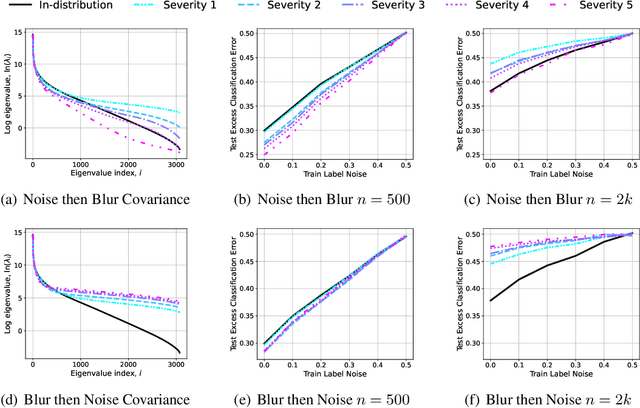
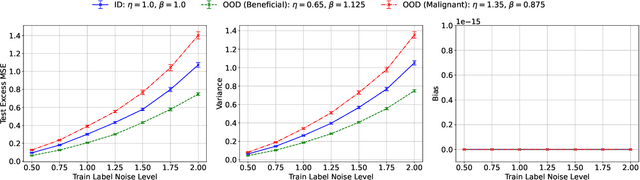
Minimum-Norm Interpolation Under Covariate Shift

Transfer learning is a critical part of real-world machine learning deployments and has been extensively studied in experimental works with overparameterized neural networks. However, even in the simplest setting of linear regression a notable gap still exists in the theoretical understanding of transfer learning. In-distribution research on high-dimensional linear regression has led to the identification of a phenomenon known as \textit{benign overfitting}, in which linear interpolators overfit to noisy training labels and yet still generalize well. This behavior occurs under specific conditions on the source covariance matrix and input data dimension. Therefore, it is natural to wonder how such high-dimensional linear models behave under transfer learning. We prove the first non-asymptotic excess risk bounds for benignly-overfit linear interpolators in the transfer learning setting. From our analysis, we propose a taxonomy of \textit{beneficial} and \textit{malignant} covariate shifts based on the degree of overparameterization. We follow our analysis with empirical studies that show these beneficial and malignant covariate shifts for linear interpolators on real image data, and for fully-connected neural networks in settings where the input data dimension is larger than the training sample size.

Benign Overfitting and Grokking in ReLU Networks for XOR Cluster Data

Neural networks trained by gradient descent (GD) have exhibited a number of surprising generalization behaviors. First, they can achieve a perfect fit to noisy training data and still generalize near-optimally, showing that overfitting can sometimes be benign. Second, they can undergo a period of classical, harmful overfitting -- achieving a perfect fit to training data with near-random performance on test data -- before transitioning ("grokking") to near-optimal generalization later in training. In this work, we show that both of these phenomena provably occur in two-layer ReLU networks trained by GD on XOR cluster data where a constant fraction of the training labels are flipped. In this setting, we show that after the first step of GD, the network achieves 100% training accuracy, perfectly fitting the noisy labels in the training data, but achieves near-random test accuracy. At a later training step, the network achieves near-optimal test accuracy while still fitting the random labels in the training data, exhibiting a "grokking" phenomenon. This provides the first theoretical result of benign overfitting in neural network classification when the data distribution is not linearly separable. Our proofs rely on analyzing the feature learning process under GD, which reveals that the network implements a non-generalizable linear classifier after one step and gradually learns generalizable features in later steps.

The Effect of SGD Batch Size on Autoencoder Learning: Sparsity, Sharpness, and Feature Learning

In this work, we investigate the dynamics of stochastic gradient descent (SGD) when training a single-neuron autoencoder with linear or ReLU activation on orthogonal data. We show that for this non-convex problem, randomly initialized SGD with a constant step size successfully finds a global minimum for any batch size choice. However, the particular global minimum found depends upon the batch size. In the full-batch setting, we show that the solution is dense (i.e., not sparse) and is highly aligned with its initialized direction, showing that relatively little feature learning occurs. On the other hand, for any batch size strictly smaller than the number of samples, SGD finds a global minimum which is sparse and nearly orthogonal to its initialization, showing that the randomness of stochastic gradients induces a qualitatively different type of "feature selection" in this setting. Moreover, if we measure the sharpness of the minimum by the trace of the Hessian, the minima found with full batch gradient descent are flatter than those found with strictly smaller batch sizes, in contrast to previous works which suggest that large batches lead to sharper minima. To prove convergence of SGD with a constant step size, we introduce a powerful tool from the theory of non-homogeneous random walks which may be of independent interest.

Trained Transformers Learn Linear Models In-Context

Attention-based neural networks such as transformers have demonstrated a remarkable ability to exhibit in-context learning (ICL): Given a short prompt sequence of tokens from an unseen task, they can formulate relevant per-token and next-token predictions without any parameter updates. By embedding a sequence of labeled training data and unlabeled test data as a prompt, this allows for transformers to behave like supervised learning algorithms. Indeed, recent work has shown that when training transformer architectures over random instances of linear regression problems, these models' predictions mimic those of ordinary least squares. Towards understanding the mechanisms underlying this phenomenon, we investigate the dynamics of ICL in transformers with a single linear self-attention layer trained by gradient flow on linear regression tasks. We show that despite non-convexity, gradient flow with a suitable random initialization finds a global minimum of the objective function. At this global minimum, when given a test prompt of labeled examples from a new prediction task, the transformer achieves prediction error competitive with the best linear predictor over the test prompt distribution. We additionally characterize the robustness of the trained transformer to a variety of distribution shifts and show that although a number of shifts are tolerated, shifts in the covariate distribution of the prompts are not. Motivated by this, we consider a generalized ICL setting where the covariate distributions can vary across prompts. We show that although gradient flow succeeds at finding a global minimum in this setting, the trained transformer is still brittle under mild covariate shifts.

Benign Overfitting in Linear Classifiers and Leaky ReLU Networks from KKT Conditions for Margin Maximization

Linear classifiers and leaky ReLU networks trained by gradient flow on the logistic loss have an implicit bias towards solutions which satisfy the Karush--Kuhn--Tucker (KKT) conditions for margin maximization. In this work we establish a number of settings where the satisfaction of these KKT conditions implies benign overfitting in linear classifiers and in two-layer leaky ReLU networks: the estimators interpolate noisy training data and simultaneously generalize well to test data. The settings include variants of the noisy class-conditional Gaussians considered in previous work as well as new distributional settings where benign overfitting has not been previously observed. The key ingredient to our proof is the observation that when the training data is nearly-orthogonal, both linear classifiers and leaky ReLU networks satisfying the KKT conditions for their respective margin maximization problems behave like a nearly uniform average of the training examples.

The Double-Edged Sword of Implicit Bias: Generalization vs. Robustness in ReLU Networks

In this work, we study the implications of the implicit bias of gradient flow on generalization and adversarial robustness in ReLU networks. We focus on a setting where the data consists of clusters and the correlations between cluster means are small, and show that in two-layer ReLU networks gradient flow is biased towards solutions that generalize well, but are highly vulnerable to adversarial examples. Our results hold even in cases where the network has many more parameters than training examples. Despite the potential for harmful overfitting in such overparameterized settings, we prove that the implicit bias of gradient flow prevents it. However, the implicit bias also leads to non-robust solutions (susceptible to small adversarial $\ell_2$-perturbations), even though robust networks that fit the data exist.

Implicit Bias in Leaky ReLU Networks Trained on High-Dimensional Data

The implicit biases of gradient-based optimization algorithms are conjectured to be a major factor in the success of modern deep learning. In this work, we investigate the implicit bias of gradient flow and gradient descent in two-layer fully-connected neural networks with leaky ReLU activations when the training data are nearly-orthogonal, a common property of high-dimensional data. For gradient flow, we leverage recent work on the implicit bias for homogeneous neural networks to show that asymptotically, gradient flow produces a neural network with rank at most two. Moreover, this network is an $\ell_2$-max-margin solution (in parameter space), and has a linear decision boundary that corresponds to an approximate-max-margin linear predictor. For gradient descent, provided the random initialization variance is small enough, we show that a single step of gradient descent suffices to drastically reduce the rank of the network, and that the rank remains small throughout training. We provide experiments which suggest that a small initialization scale is important for finding low-rank neural networks with gradient descent.