Adversarial Robustness of In-Context Learning in Transformers for Linear Regression

Transformers have demonstrated remarkable in-context learning capabilities across various domains, including statistical learning tasks. While previous work has shown that transformers can implement common learning algorithms, the adversarial robustness of these learned algorithms remains unexplored. This work investigates the vulnerability of in-context learning in transformers to \textit{hijacking attacks} focusing on the setting of linear regression tasks. Hijacking attacks are prompt-manipulation attacks in which the adversary's goal is to manipulate the prompt to force the transformer to generate a specific output. We first prove that single-layer linear transformers, known to implement gradient descent in-context, are non-robust and can be manipulated to output arbitrary predictions by perturbing a single example in the in-context training set. While our experiments show these attacks succeed on linear transformers, we find they do not transfer to more complex transformers with GPT-2 architectures. Nonetheless, we show that these transformers can be hijacked using gradient-based adversarial attacks. We then demonstrate that adversarial training enhances transformers' robustness against hijacking attacks, even when just applied during finetuning. Additionally, we find that in some settings, adversarial training against a weaker attack model can lead to robustness to a stronger attack model. Lastly, we investigate the transferability of hijacking attacks across transformers of varying scales and initialization seeds, as well as between transformers and ordinary least squares (OLS). We find that while attacks transfer effectively between small-scale transformers, they show poor transferability in other scenarios (small-to-large scale, large-to-large scale, and between transformers and OLS).

Weight decay induces low-rank attention layers

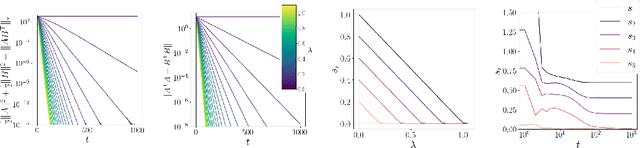
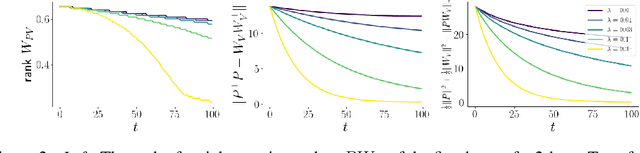
The effect of regularizers such as weight decay when training deep neural networks is not well understood. We study the influence of weight decay as well as $L2$-regularization when training neural network models in which parameter matrices interact multiplicatively. This combination is of particular interest as this parametrization is common in attention layers, the workhorse of transformers. Here, key-query, as well as value-projection parameter matrices, are multiplied directly with each other: $W_K^TW_Q$ and $PW_V$. We extend previous results and show on one hand that any local minimum of a $L2$-regularized loss of the form $L(AB^\top) + \lambda (\|A\|^2 + \|B\|^2)$ coincides with a minimum of the nuclear norm-regularized loss $L(AB^\top) + \lambda\|AB^\top\|_*$, and on the other hand that the 2 losses become identical exponentially quickly during training. We thus complement existing works linking $L2$-regularization with low-rank regularization, and in particular, explain why such regularization on the matrix product affects early stages of training. Based on these theoretical insights, we verify empirically that the key-query and value-projection matrix products $W_K^TW_Q, PW_V$ within attention layers, when optimized with weight decay, as usually done in vision tasks and language modelling, indeed induce a significant reduction in the rank of $W_K^TW_Q$ and $PW_V$, even in fully online training. We find that, in accordance with existing work, inducing low rank in attention matrix products can damage language model performance, and observe advantages when decoupling weight decay in attention layers from the rest of the parameters.