Scale leads to compositional generalization

Can neural networks systematically capture discrete, compositional task structure despite their continuous, distributed nature? The impressive capabilities of large-scale neural networks suggest that the answer to this question is yes. However, even for the most capable models, there are still frequent failure cases that raise doubts about their compositionality. Here, we seek to understand what it takes for a standard neural network to generalize over tasks that share compositional structure. We find that simply scaling data and model size leads to compositional generalization. We show that this holds across different task encodings as long as the training distribution sufficiently covers the task space. In line with this finding, we prove that standard multilayer perceptrons can approximate a general class of compositional task families to arbitrary precision using only a linear number of neurons with respect to the number of task modules. Finally, we uncover that if networks successfully compositionally generalize, the constituents of a task can be linearly decoded from their hidden activations. We show that this metric correlates with failures of text-to-image generation models to compose known concepts.

Weight decay induces low-rank attention layers

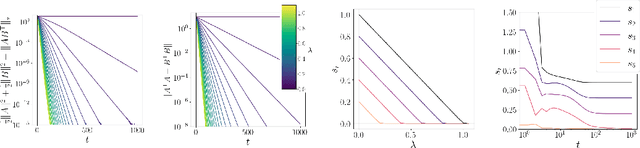
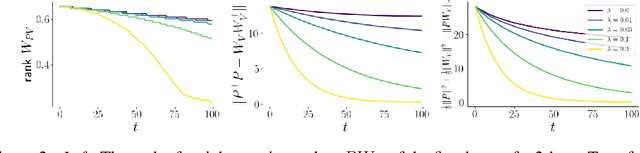
The effect of regularizers such as weight decay when training deep neural networks is not well understood. We study the influence of weight decay as well as $L2$-regularization when training neural network models in which parameter matrices interact multiplicatively. This combination is of particular interest as this parametrization is common in attention layers, the workhorse of transformers. Here, key-query, as well as value-projection parameter matrices, are multiplied directly with each other: $W_K^TW_Q$ and $PW_V$. We extend previous results and show on one hand that any local minimum of a $L2$-regularized loss of the form $L(AB^\top) + \lambda (\|A\|^2 + \|B\|^2)$ coincides with a minimum of the nuclear norm-regularized loss $L(AB^\top) + \lambda\|AB^\top\|_*$, and on the other hand that the 2 losses become identical exponentially quickly during training. We thus complement existing works linking $L2$-regularization with low-rank regularization, and in particular, explain why such regularization on the matrix product affects early stages of training. Based on these theoretical insights, we verify empirically that the key-query and value-projection matrix products $W_K^TW_Q, PW_V$ within attention layers, when optimized with weight decay, as usually done in vision tasks and language modelling, indeed induce a significant reduction in the rank of $W_K^TW_Q$ and $PW_V$, even in fully online training. We find that, in accordance with existing work, inducing low rank in attention matrix products can damage language model performance, and observe advantages when decoupling weight decay in attention layers from the rest of the parameters.

Learning Randomized Algorithms with Transformers

Randomization is a powerful tool that endows algorithms with remarkable properties. For instance, randomized algorithms excel in adversarial settings, often surpassing the worst-case performance of deterministic algorithms with large margins. Furthermore, their success probability can be amplified by simple strategies such as repetition and majority voting. In this paper, we enhance deep neural networks, in particular transformer models, with randomization. We demonstrate for the first time that randomized algorithms can be instilled in transformers through learning, in a purely data- and objective-driven manner. First, we analyze known adversarial objectives for which randomized algorithms offer a distinct advantage over deterministic ones. We then show that common optimization techniques, such as gradient descent or evolutionary strategies, can effectively learn transformer parameters that make use of the randomness provided to the model. To illustrate the broad applicability of randomization in empowering neural networks, we study three conceptual tasks: associative recall, graph coloring, and agents that explore grid worlds. In addition to demonstrating increased robustness against oblivious adversaries through learned randomization, our experiments reveal remarkable performance improvements due to the inherently random nature of the neural networks' computation and predictions.

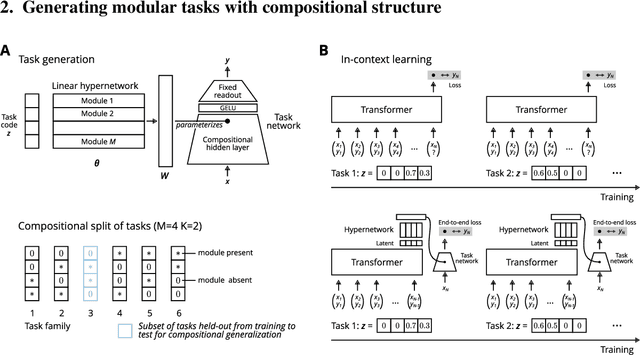
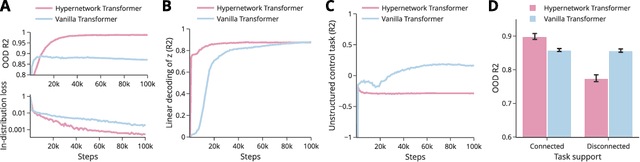
When can transformers compositionally generalize in-context?

Many tasks can be composed from a few independent components. This gives rise to a combinatorial explosion of possible tasks, only some of which might be encountered during training. Under what circumstances can transformers compositionally generalize from a subset of tasks to all possible combinations of tasks that share similar components? Here we study a modular multitask setting that allows us to precisely control compositional structure in the data generation process. We present evidence that transformers learning in-context struggle to generalize compositionally on this task despite being in principle expressive enough to do so. Compositional generalization becomes possible only when introducing a bottleneck that enforces an explicit separation between task inference and task execution.

Attention as a Hypernetwork

Transformers can under some circumstances generalize to novel problem instances whose constituent parts might have been encountered during training but whose compositions have not. What mechanisms underlie this ability for compositional generalization? By reformulating multi-head attention as a hypernetwork, we reveal that a low-dimensional latent code specifies key-query specific operations. We find empirically that this latent code is highly structured, capturing information about the subtasks performed by the network. Using the framework of attention as a hypernetwork we further propose a simple modification of multi-head linear attention that strengthens the ability for compositional generalization on a range of abstract reasoning tasks. In particular, we introduce a symbolic version of the Raven Progressive Matrices human intelligence test on which we demonstrate how scaling model size and data enables compositional generalization and gives rise to a functionally structured latent code in the transformer.

Discovering modular solutions that generalize compositionally

Many complex tasks and environments can be decomposed into simpler, independent parts. Discovering such underlying compositional structure has the potential to expedite adaptation and enable compositional generalization. Despite progress, our most powerful systems struggle to compose flexibly. While most of these systems are monolithic, modularity promises to allow capturing the compositional nature of many tasks. However, it is unclear under which circumstances modular systems discover this hidden compositional structure. To shed light on this question, we study a teacher-student setting with a modular teacher where we have full control over the composition of ground truth modules. This allows us to relate the problem of compositional generalization to that of identification of the underlying modules. We show theoretically that identification up to linear transformation purely from demonstrations is possible in hypernetworks without having to learn an exponential number of module combinations. While our theory assumes the infinite data limit, in an extensive empirical study we demonstrate how meta-learning from finite data can discover modular solutions that generalize compositionally in modular but not monolithic architectures. We further show that our insights translate outside the teacher-student setting and demonstrate that in tasks with compositional preferences and tasks with compositional goals hypernetworks can discover modular policies that compositionally generalize.

Gated recurrent neural networks discover attention

Recent architectural developments have enabled recurrent neural networks (RNNs) to reach and even surpass the performance of Transformers on certain sequence modeling tasks. These modern RNNs feature a prominent design pattern: linear recurrent layers interconnected by feedforward paths with multiplicative gating. Here, we show how RNNs equipped with these two design elements can exactly implement (linear) self-attention, the main building block of Transformers. By reverse-engineering a set of trained RNNs, we find that gradient descent in practice discovers our construction. In particular, we examine RNNs trained to solve simple in-context learning tasks on which Transformers are known to excel and find that gradient descent instills in our RNNs the same attention-based in-context learning algorithm used by Transformers. Our findings highlight the importance of multiplicative interactions in neural networks and suggest that certain RNNs might be unexpectedly implementing attention under the hood.

Random initialisations performing above chance and how to find them

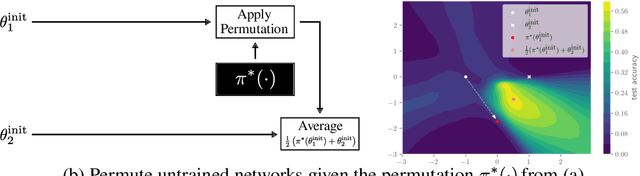
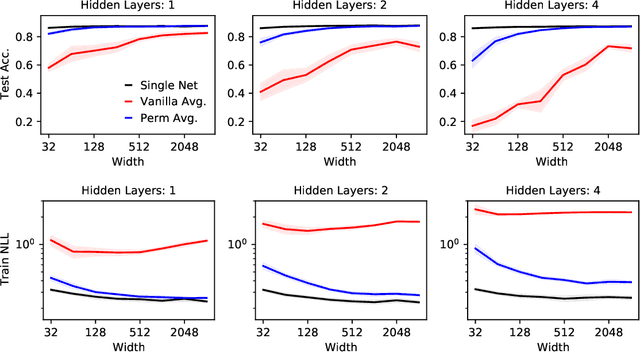
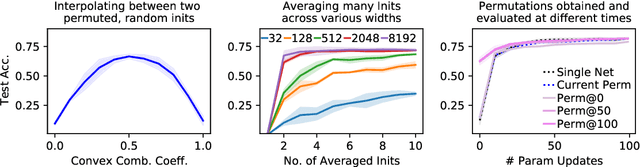
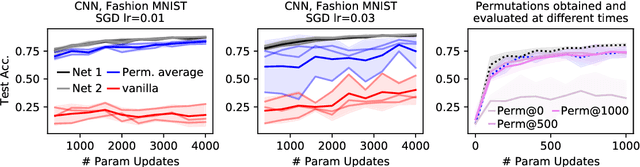
Neural networks trained with stochastic gradient descent (SGD) starting from different random initialisations typically find functionally very similar solutions, raising the question of whether there are meaningful differences between different SGD solutions. Entezari et al. recently conjectured that despite different initialisations, the solutions found by SGD lie in the same loss valley after taking into account the permutation invariance of neural networks. Concretely, they hypothesise that any two solutions found by SGD can be permuted such that the linear interpolation between their parameters forms a path without significant increases in loss. Here, we use a simple but powerful algorithm to find such permutations that allows us to obtain direct empirical evidence that the hypothesis is true in fully connected networks. Strikingly, we find that two networks already live in the same loss valley at the time of initialisation and averaging their random, but suitably permuted initialisation performs significantly above chance. In contrast, for convolutional architectures, our evidence suggests that the hypothesis does not hold. Especially in a large learning rate regime, SGD seems to discover diverse modes.