Multi-agent cooperation through learning-aware policy gradients

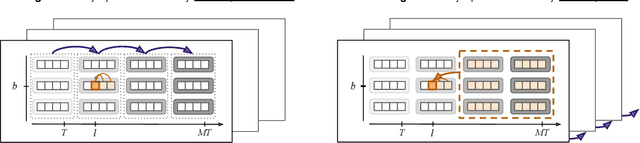
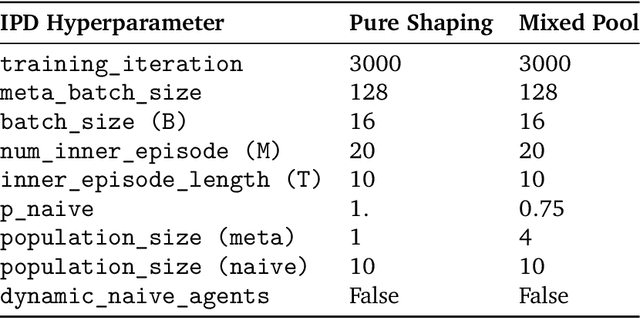
Self-interested individuals often fail to cooperate, posing a fundamental challenge for multi-agent learning. How can we achieve cooperation among self-interested, independent learning agents? Promising recent work has shown that in certain tasks cooperation can be established between learning-aware agents who model the learning dynamics of each other. Here, we present the first unbiased, higher-derivative-free policy gradient algorithm for learning-aware reinforcement learning, which takes into account that other agents are themselves learning through trial and error based on multiple noisy trials. We then leverage efficient sequence models to condition behavior on long observation histories that contain traces of the learning dynamics of other agents. Training long-context policies with our algorithm leads to cooperative behavior and high returns on standard social dilemmas, including a challenging environment where temporally-extended action coordination is required. Finally, we derive from the iterated prisoner's dilemma a novel explanation for how and when cooperation arises among self-interested learning-aware agents.

Learning Randomized Algorithms with Transformers

Randomization is a powerful tool that endows algorithms with remarkable properties. For instance, randomized algorithms excel in adversarial settings, often surpassing the worst-case performance of deterministic algorithms with large margins. Furthermore, their success probability can be amplified by simple strategies such as repetition and majority voting. In this paper, we enhance deep neural networks, in particular transformer models, with randomization. We demonstrate for the first time that randomized algorithms can be instilled in transformers through learning, in a purely data- and objective-driven manner. First, we analyze known adversarial objectives for which randomized algorithms offer a distinct advantage over deterministic ones. We then show that common optimization techniques, such as gradient descent or evolutionary strategies, can effectively learn transformer parameters that make use of the randomness provided to the model. To illustrate the broad applicability of randomization in empowering neural networks, we study three conceptual tasks: associative recall, graph coloring, and agents that explore grid worlds. In addition to demonstrating increased robustness against oblivious adversaries through learned randomization, our experiments reveal remarkable performance improvements due to the inherently random nature of the neural networks' computation and predictions.

When can transformers compositionally generalize in-context?

Many tasks can be composed from a few independent components. This gives rise to a combinatorial explosion of possible tasks, only some of which might be encountered during training. Under what circumstances can transformers compositionally generalize from a subset of tasks to all possible combinations of tasks that share similar components? Here we study a modular multitask setting that allows us to precisely control compositional structure in the data generation process. We present evidence that transformers learning in-context struggle to generalize compositionally on this task despite being in principle expressive enough to do so. Compositional generalization becomes possible only when introducing a bottleneck that enforces an explicit separation between task inference and task execution.

State Soup: In-Context Skill Learning, Retrieval and Mixing

A new breed of gated-linear recurrent neural networks has reached state-of-the-art performance on a range of sequence modeling problems. Such models naturally handle long sequences efficiently, as the cost of processing a new input is independent of sequence length. Here, we explore another advantage of these stateful sequence models, inspired by the success of model merging through parameter interpolation. Building on parallels between fine-tuning and in-context learning, we investigate whether we can treat internal states as task vectors that can be stored, retrieved, and then linearly combined, exploiting the linearity of recurrence. We study this form of fast model merging on Mamba-2.8b, a pretrained recurrent model, and present preliminary evidence that simple linear state interpolation methods suffice to improve next-token perplexity as well as downstream in-context learning task performance.

Linear Transformers are Versatile In-Context Learners

Recent research has demonstrated that transformers, particularly linear attention models, implicitly execute gradient-descent-like algorithms on data provided in-context during their forward inference step. However, their capability in handling more complex problems remains unexplored. In this paper, we prove that any linear transformer maintains an implicit linear model and can be interpreted as performing a variant of preconditioned gradient descent. We also investigate the use of linear transformers in a challenging scenario where the training data is corrupted with different levels of noise. Remarkably, we demonstrate that for this problem linear transformers discover an intricate and highly effective optimization algorithm, surpassing or matching in performance many reasonable baselines. We reverse-engineer this algorithm and show that it is a novel approach incorporating momentum and adaptive rescaling based on noise levels. Our findings show that even linear transformers possess the surprising ability to discover sophisticated optimization strategies.

Discovering modular solutions that generalize compositionally

Many complex tasks and environments can be decomposed into simpler, independent parts. Discovering such underlying compositional structure has the potential to expedite adaptation and enable compositional generalization. Despite progress, our most powerful systems struggle to compose flexibly. While most of these systems are monolithic, modularity promises to allow capturing the compositional nature of many tasks. However, it is unclear under which circumstances modular systems discover this hidden compositional structure. To shed light on this question, we study a teacher-student setting with a modular teacher where we have full control over the composition of ground truth modules. This allows us to relate the problem of compositional generalization to that of identification of the underlying modules. We show theoretically that identification up to linear transformation purely from demonstrations is possible in hypernetworks without having to learn an exponential number of module combinations. While our theory assumes the infinite data limit, in an extensive empirical study we demonstrate how meta-learning from finite data can discover modular solutions that generalize compositionally in modular but not monolithic architectures. We further show that our insights translate outside the teacher-student setting and demonstrate that in tasks with compositional preferences and tasks with compositional goals hypernetworks can discover modular policies that compositionally generalize.

Uncovering mesa-optimization algorithms in Transformers

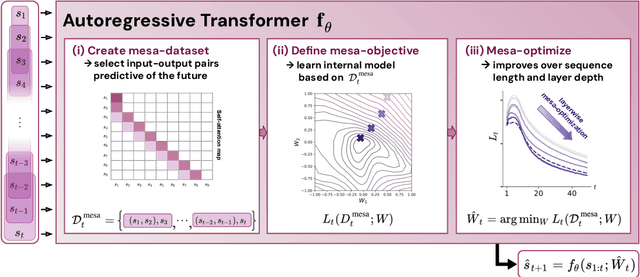
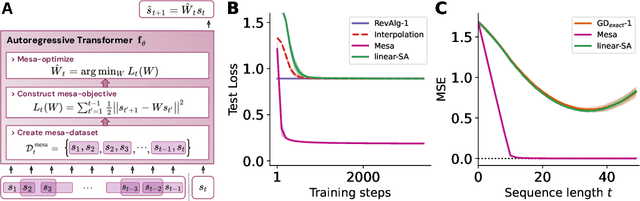
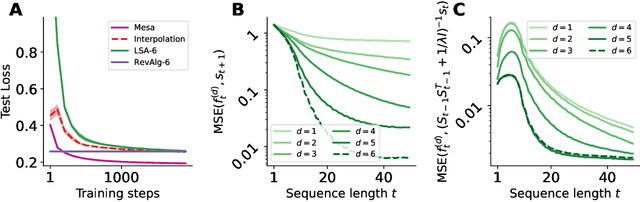
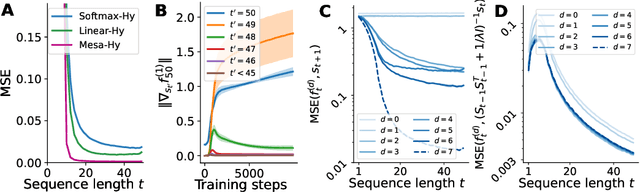
Transformers have become the dominant model in deep learning, but the reason for their superior performance is poorly understood. Here, we hypothesize that the strong performance of Transformers stems from an architectural bias towards mesa-optimization, a learned process running within the forward pass of a model consisting of the following two steps: (i) the construction of an internal learning objective, and (ii) its corresponding solution found through optimization. To test this hypothesis, we reverse-engineer a series of autoregressive Transformers trained on simple sequence modeling tasks, uncovering underlying gradient-based mesa-optimization algorithms driving the generation of predictions. Moreover, we show that the learned forward-pass optimization algorithm can be immediately repurposed to solve supervised few-shot tasks, suggesting that mesa-optimization might underlie the in-context learning capabilities of large language models. Finally, we propose a novel self-attention layer, the mesa-layer, that explicitly and efficiently solves optimization problems specified in context. We find that this layer can lead to improved performance in synthetic and preliminary language modeling experiments, adding weight to our hypothesis that mesa-optimization is an important operation hidden within the weights of trained Transformers.

Gated recurrent neural networks discover attention

Recent architectural developments have enabled recurrent neural networks (RNNs) to reach and even surpass the performance of Transformers on certain sequence modeling tasks. These modern RNNs feature a prominent design pattern: linear recurrent layers interconnected by feedforward paths with multiplicative gating. Here, we show how RNNs equipped with these two design elements can exactly implement (linear) self-attention, the main building block of Transformers. By reverse-engineering a set of trained RNNs, we find that gradient descent in practice discovers our construction. In particular, we examine RNNs trained to solve simple in-context learning tasks on which Transformers are known to excel and find that gradient descent instills in our RNNs the same attention-based in-context learning algorithm used by Transformers. Our findings highlight the importance of multiplicative interactions in neural networks and suggest that certain RNNs might be unexpectedly implementing attention under the hood.

Transformers learn in-context by gradient descent

Transformers have become the state-of-the-art neural network architecture across numerous domains of machine learning. This is partly due to their celebrated ability to transfer and to learn in-context based on few examples. Nevertheless, the mechanisms by which Transformers become in-context learners are not well understood and remain mostly an intuition. Here, we argue that training Transformers on auto-regressive tasks can be closely related to well-known gradient-based meta-learning formulations. We start by providing a simple weight construction that shows the equivalence of data transformations induced by 1) a single linear self-attention layer and by 2) gradient-descent (GD) on a regression loss. Motivated by that construction, we show empirically that when training self-attention-only Transformers on simple regression tasks either the models learned by GD and Transformers show great similarity or, remarkably, the weights found by optimization match the construction. Thus we show how trained Transformers implement gradient descent in their forward pass. This allows us, at least in the domain of regression problems, to mechanistically understand the inner workings of optimized Transformers that learn in-context. Furthermore, we identify how Transformers surpass plain gradient descent by an iterative curvature correction and learn linear models on deep data representations to solve non-linear regression tasks. Finally, we discuss intriguing parallels to a mechanism identified to be crucial for in-context learning termed induction-head (Olsson et al., 2022) and show how it could be understood as a specific case of in-context learning by gradient descent learning within Transformers.

Disentangling the Predictive Variance of Deep Ensembles through the Neural Tangent Kernel

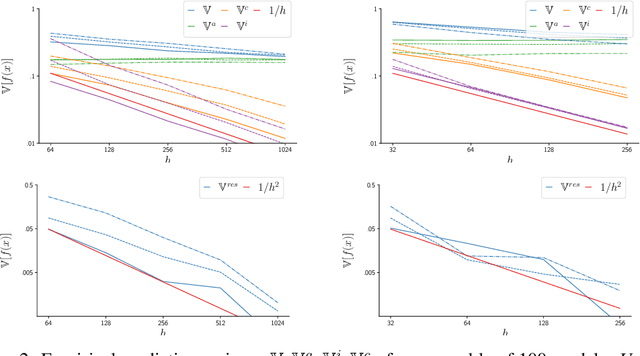
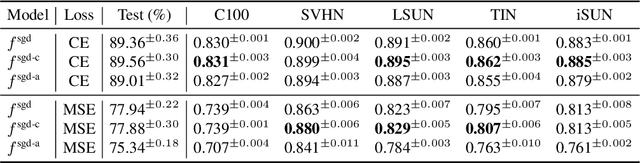
Identifying unfamiliar inputs, also known as out-of-distribution (OOD) detection, is a crucial property of any decision making process. A simple and empirically validated technique is based on deep ensembles where the variance of predictions over different neural networks acts as a substitute for input uncertainty. Nevertheless, a theoretical understanding of the inductive biases leading to the performance of deep ensemble's uncertainty estimation is missing. To improve our description of their behavior, we study deep ensembles with large layer widths operating in simplified linear training regimes, in which the functions trained with gradient descent can be described by the neural tangent kernel. We identify two sources of noise, each inducing a distinct inductive bias in the predictive variance at initialization. We further show theoretically and empirically that both noise sources affect the predictive variance of non-linear deep ensembles in toy models and realistic settings after training. Finally, we propose practical ways to eliminate part of these noise sources leading to significant changes and improved OOD detection in trained deep ensembles.