A game theory for foundation models shows new paths to rational cooperation through similarity inference

As autonomous agents powered by foundation models are increasingly integrated into social and economic systems, understanding the principles governing their collective behavior is essential for ensuring safety and cooperation. Classical game theory, the dominant framework for modeling rational interaction, is built upon the assumption of `decoupled agency,' where agents treat their own decision-making as independent of the environment and other actors. Modern AI agents, however, jointly predict their own future actions alongside external observations. Here, we report a striking finding: when interacting in stylized social dilemmas, foundation model agents engaging in optimal planning consistently converge to stable cooperation, directly contradicting classical game-theoretic predictions of mutual defection. To understand this phenomenon, we introduce the `embedded Bayesian agent,' a theoretical model for foundation model agents. By shifting from decoupled to embedded agency, these agents model themselves as part of the universe they inhabit, maintaining epistemic uncertainty about their own decision-making algorithms. We show that by inferring whether others are behaviorally similar, an embedded agent treats its own deliberation during planning as evidence: a decision to cooperate predicts a similar decision by a similar partner. We formalize this mechanism of similarity inference through the `embedded equilibrium,' a novel solution concept replacing the Nash equilibrium to provide a foundational game theory for the social behavior of modern AI agents.

Emergent temporal abstractions in autoregressive models enable hierarchical reinforcement learning

Large-scale autoregressive models pretrained on next-token prediction and finetuned with reinforcement learning (RL) have achieved unprecedented success on many problem domains. During RL, these models explore by generating new outputs, one token at a time. However, sampling actions token-by-token can result in highly inefficient learning, particularly when rewards are sparse. Here, we show that it is possible to overcome this problem by acting and exploring within the internal representations of an autoregressive model. Specifically, to discover temporally-abstract actions, we introduce a higher-order, non-causal sequence model whose outputs control the residual stream activations of a base autoregressive model. On grid world and MuJoCo-based tasks with hierarchical structure, we find that the higher-order model learns to compress long activation sequence chunks onto internal controllers. Critically, each controller executes a sequence of behaviorally meaningful actions that unfold over long timescales and are accompanied with a learned termination condition, such that composing multiple controllers over time leads to efficient exploration on novel tasks. We show that direct internal controller reinforcement, a process we term "internal RL", enables learning from sparse rewards in cases where standard RL finetuning fails. Our results demonstrate the benefits of latent action generation and reinforcement in autoregressive models, suggesting internal RL as a promising avenue for realizing hierarchical RL within foundation models.

Learning Randomized Algorithms with Transformers

Randomization is a powerful tool that endows algorithms with remarkable properties. For instance, randomized algorithms excel in adversarial settings, often surpassing the worst-case performance of deterministic algorithms with large margins. Furthermore, their success probability can be amplified by simple strategies such as repetition and majority voting. In this paper, we enhance deep neural networks, in particular transformer models, with randomization. We demonstrate for the first time that randomized algorithms can be instilled in transformers through learning, in a purely data- and objective-driven manner. First, we analyze known adversarial objectives for which randomized algorithms offer a distinct advantage over deterministic ones. We then show that common optimization techniques, such as gradient descent or evolutionary strategies, can effectively learn transformer parameters that make use of the randomness provided to the model. To illustrate the broad applicability of randomization in empowering neural networks, we study three conceptual tasks: associative recall, graph coloring, and agents that explore grid worlds. In addition to demonstrating increased robustness against oblivious adversaries through learned randomization, our experiments reveal remarkable performance improvements due to the inherently random nature of the neural networks' computation and predictions.

Discovering modular solutions that generalize compositionally

Many complex tasks and environments can be decomposed into simpler, independent parts. Discovering such underlying compositional structure has the potential to expedite adaptation and enable compositional generalization. Despite progress, our most powerful systems struggle to compose flexibly. While most of these systems are monolithic, modularity promises to allow capturing the compositional nature of many tasks. However, it is unclear under which circumstances modular systems discover this hidden compositional structure. To shed light on this question, we study a teacher-student setting with a modular teacher where we have full control over the composition of ground truth modules. This allows us to relate the problem of compositional generalization to that of identification of the underlying modules. We show theoretically that identification up to linear transformation purely from demonstrations is possible in hypernetworks without having to learn an exponential number of module combinations. While our theory assumes the infinite data limit, in an extensive empirical study we demonstrate how meta-learning from finite data can discover modular solutions that generalize compositionally in modular but not monolithic architectures. We further show that our insights translate outside the teacher-student setting and demonstrate that in tasks with compositional preferences and tasks with compositional goals hypernetworks can discover modular policies that compositionally generalize.

Gated recurrent neural networks discover attention

Recent architectural developments have enabled recurrent neural networks (RNNs) to reach and even surpass the performance of Transformers on certain sequence modeling tasks. These modern RNNs feature a prominent design pattern: linear recurrent layers interconnected by feedforward paths with multiplicative gating. Here, we show how RNNs equipped with these two design elements can exactly implement (linear) self-attention, the main building block of Transformers. By reverse-engineering a set of trained RNNs, we find that gradient descent in practice discovers our construction. In particular, we examine RNNs trained to solve simple in-context learning tasks on which Transformers are known to excel and find that gradient descent instills in our RNNs the same attention-based in-context learning algorithm used by Transformers. Our findings highlight the importance of multiplicative interactions in neural networks and suggest that certain RNNs might be unexpectedly implementing attention under the hood.

Random initialisations performing above chance and how to find them

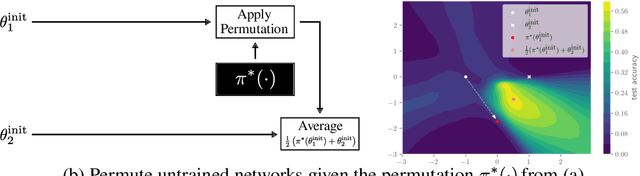
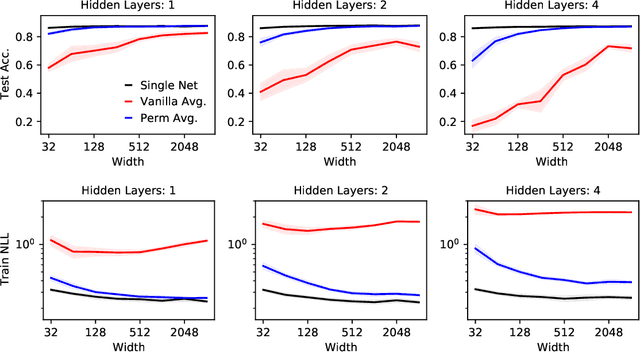
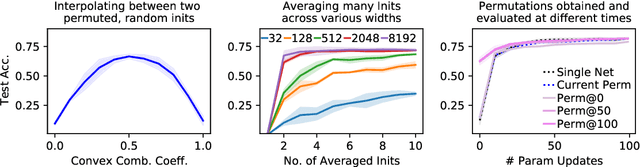
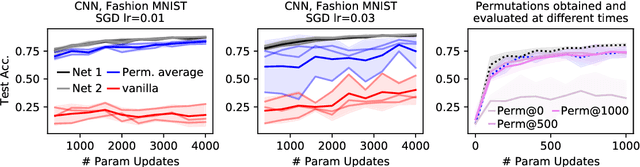
Neural networks trained with stochastic gradient descent (SGD) starting from different random initialisations typically find functionally very similar solutions, raising the question of whether there are meaningful differences between different SGD solutions. Entezari et al. recently conjectured that despite different initialisations, the solutions found by SGD lie in the same loss valley after taking into account the permutation invariance of neural networks. Concretely, they hypothesise that any two solutions found by SGD can be permuted such that the linear interpolation between their parameters forms a path without significant increases in loss. Here, we use a simple but powerful algorithm to find such permutations that allows us to obtain direct empirical evidence that the hypothesis is true in fully connected networks. Strikingly, we find that two networks already live in the same loss valley at the time of initialisation and averaging their random, but suitably permuted initialisation performs significantly above chance. In contrast, for convolutional architectures, our evidence suggests that the hypothesis does not hold. Especially in a large learning rate regime, SGD seems to discover diverse modes.

Evaluating Disentanglement of Structured Latent Representations

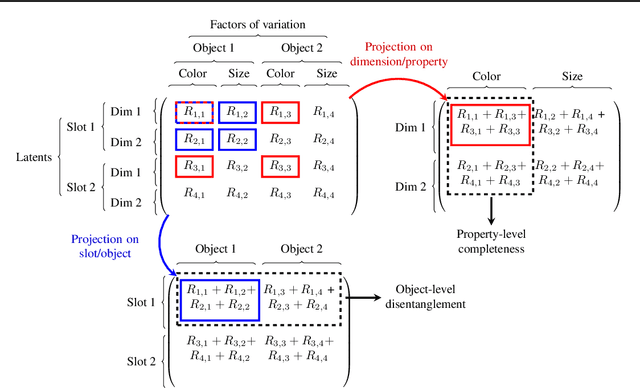
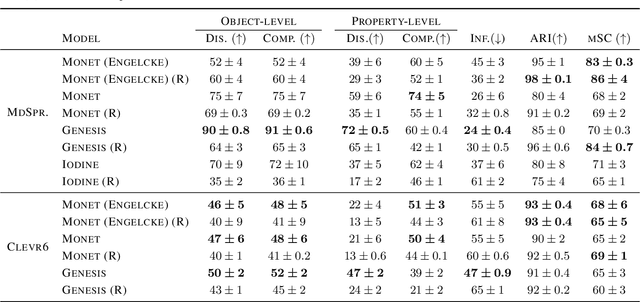
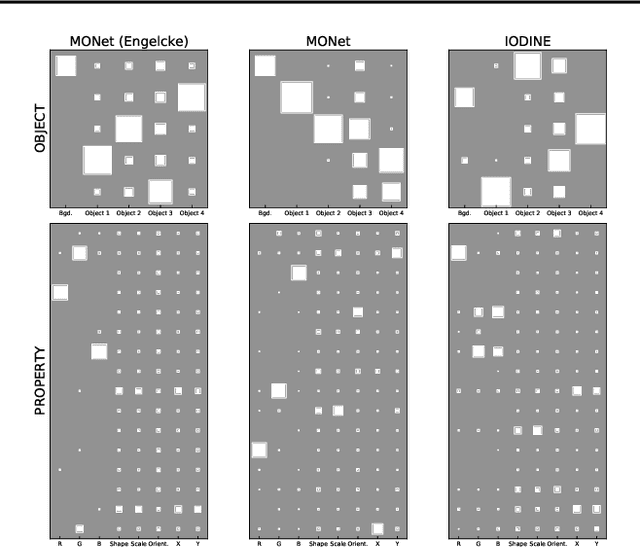
We design the first multi-layer disentanglement metric operating at all hierarchy levels of a structured latent representation, and derive its theoretical properties. Applied to object-centric representations, our metric unifies the evaluation of both object separation between latent slots and internal slot disentanglement into a common mathematical framework. It also addresses the problematic dependence on segmentation mask sharpness of previous pixel-level segmentation metrics such as ARI. Perhaps surprisingly, our experimental results show that good ARI values do not guarantee a disentangled representation, and that the exclusive focus on this metric has led to counterproductive choices in some previous evaluations. As an additional technical contribution, we present a new algorithm for obtaining feature importances that handles slot permutation invariance in the representation.

Improving Gradient Estimation in Evolutionary Strategies With Past Descent Directions

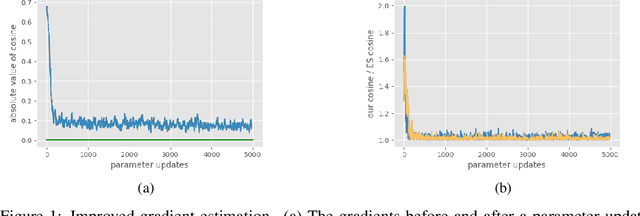
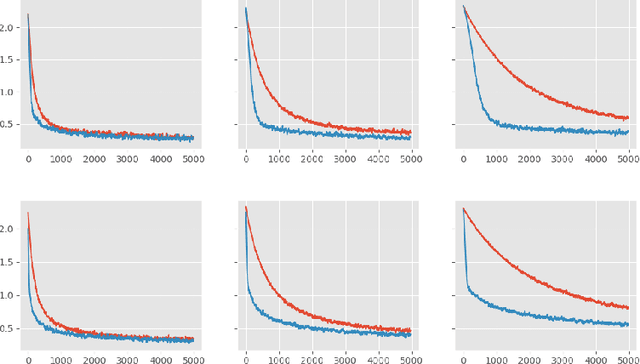
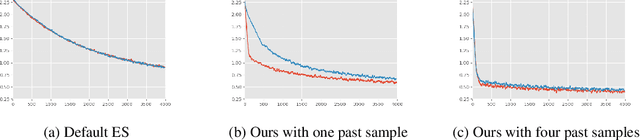
Evolutionary Strategies (ES) are known to be an effective black-box optimization technique for deep neural networks when the true gradients cannot be computed, such as in Reinforcement Learning. We continue a recent line of research that uses surrogate gradients to improve the gradient estimation of ES. We propose a novel method to optimally incorporate surrogate gradient information. Our approach, unlike previous work, needs no information about the quality of the surrogate gradients and is always guaranteed to find a descent direction that is better than the surrogate gradient. This allows to iteratively use the previous gradient estimate as surrogate gradient for the current search point. We theoretically prove that this yields fast convergence to the true gradient for linear functions and show under simplifying assumptions that it significantly improves gradient estimates for general functions. Finally, we evaluate our approach empirically on MNIST and reinforcement learning tasks and show that it considerably improves the gradient estimation of ES at no extra computational cost.

Decoupling Hierarchical Recurrent Neural Networks With Locally Computable Losses

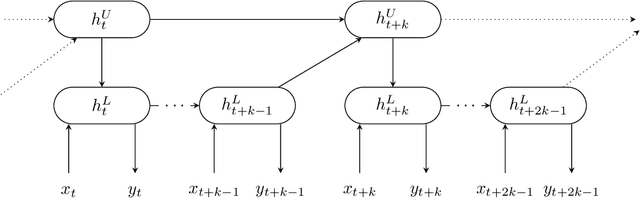
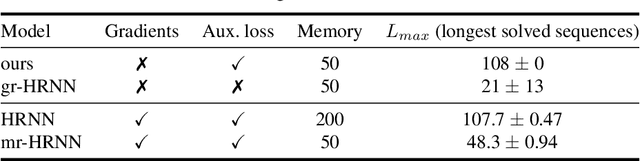
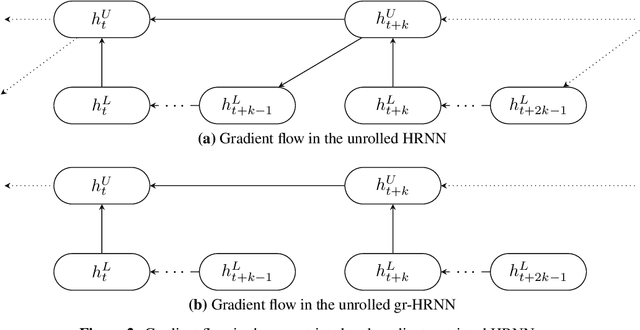
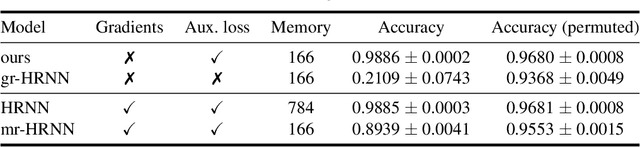
Learning long-term dependencies is a key long-standing challenge of recurrent neural networks (RNNs). Hierarchical recurrent neural networks (HRNNs) have been considered a promising approach as long-term dependencies are resolved through shortcuts up and down the hierarchy. Yet, the memory requirements of Truncated Backpropagation Through Time (TBPTT) still prevent training them on very long sequences. In this paper, we empirically show that in (deep) HRNNs, propagating gradients back from higher to lower levels can be replaced by locally computable losses, without harming the learning capability of the network, over a wide range of tasks. This decoupling by local losses reduces the memory requirements of training by a factor exponential in the depth of the hierarchy in comparison to standard TBPTT.

Optimal Kronecker-Sum Approximation of Real Time Recurrent Learning

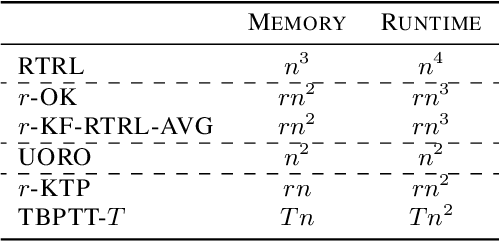
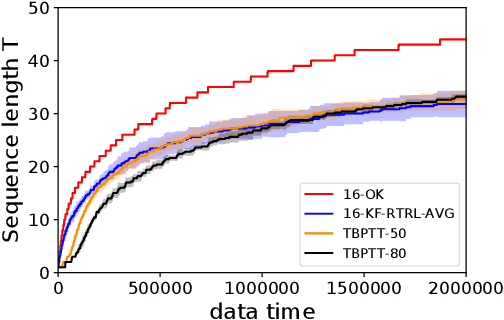
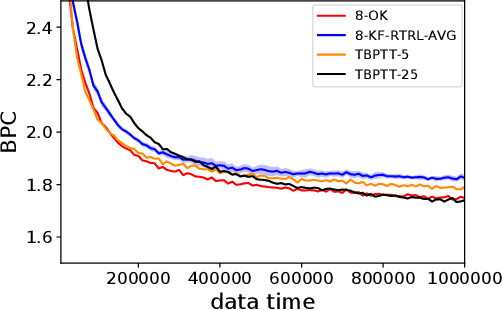
One of the central goals of Recurrent Neural Networks (RNNs) is to learn long-term dependencies in sequential data. Nevertheless, the most popular training method, Truncated Backpropagation through Time (TBPTT), categorically forbids learning dependencies beyond the truncation horizon. In contrast, the online training algorithm Real Time Recurrent Learning (RTRL) provides untruncated gradients, with the disadvantage of impractically large computational costs. Recently published approaches reduce these costs by providing noisy approximations of RTRL. We present a new approximation algorithm of RTRL, Optimal Kronecker-Sum Approximation (OK). We prove that OK is optimal for a class of approximations of RTRL, which includes all approaches published so far. Additionally, we show that OK has empirically negligible noise: Unlike previous algorithms it matches TBPTT in a real world task (character-level Penn TreeBank) and can exploit online parameter updates to outperform TBPTT in a synthetic string memorization task.