Improving Gradient Estimation in Evolutionary Strategies With Past Descent Directions
Paper and Code
Oct 11, 2019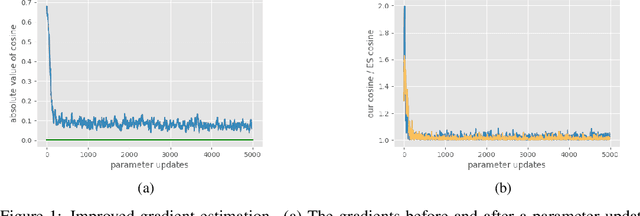

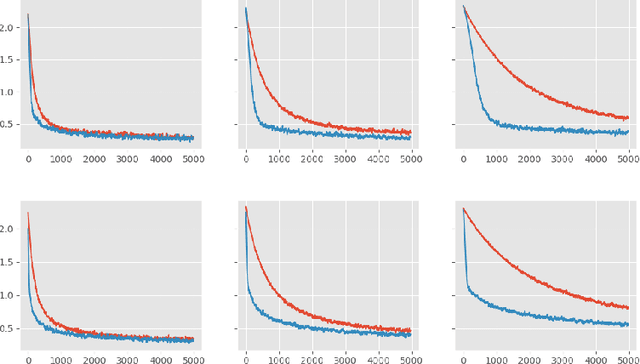
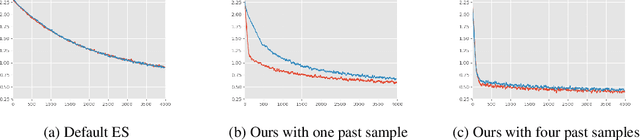
Evolutionary Strategies (ES) are known to be an effective black-box optimization technique for deep neural networks when the true gradients cannot be computed, such as in Reinforcement Learning. We continue a recent line of research that uses surrogate gradients to improve the gradient estimation of ES. We propose a novel method to optimally incorporate surrogate gradient information. Our approach, unlike previous work, needs no information about the quality of the surrogate gradients and is always guaranteed to find a descent direction that is better than the surrogate gradient. This allows to iteratively use the previous gradient estimate as surrogate gradient for the current search point. We theoretically prove that this yields fast convergence to the true gradient for linear functions and show under simplifying assumptions that it significantly improves gradient estimates for general functions. Finally, we evaluate our approach empirically on MNIST and reinforcement learning tasks and show that it considerably improves the gradient estimation of ES at no extra computational cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge