Improving Gradient Estimation in Evolutionary Strategies With Past Descent Directions

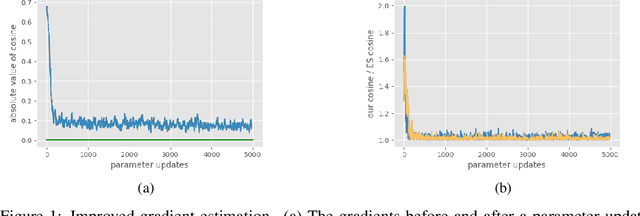
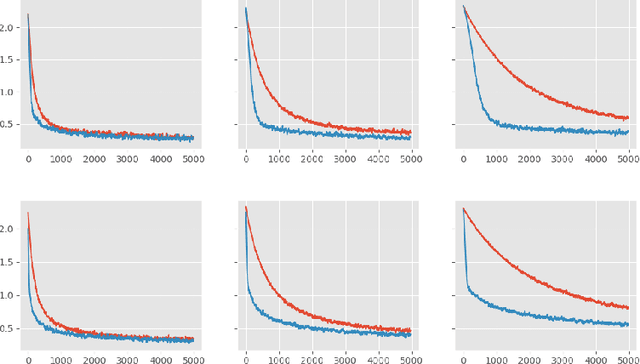
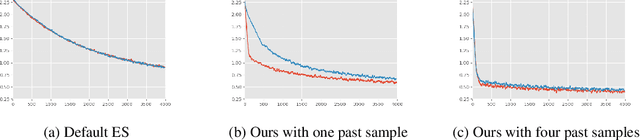
Evolutionary Strategies (ES) are known to be an effective black-box optimization technique for deep neural networks when the true gradients cannot be computed, such as in Reinforcement Learning. We continue a recent line of research that uses surrogate gradients to improve the gradient estimation of ES. We propose a novel method to optimally incorporate surrogate gradient information. Our approach, unlike previous work, needs no information about the quality of the surrogate gradients and is always guaranteed to find a descent direction that is better than the surrogate gradient. This allows to iteratively use the previous gradient estimate as surrogate gradient for the current search point. We theoretically prove that this yields fast convergence to the true gradient for linear functions and show under simplifying assumptions that it significantly improves gradient estimates for general functions. Finally, we evaluate our approach empirically on MNIST and reinforcement learning tasks and show that it considerably improves the gradient estimation of ES at no extra computational cost.

The linear hidden subset problem for the EA with scheduled and adaptive mutation rates

We study unbiased $(1+1)$ evolutionary algorithms on linear functions with an unknown number $n$ of bits with non-zero weight. Static algorithms achieve an optimal runtime of $O(n (\ln n)^{2+\epsilon})$, however, it remained unclear whether more dynamic parameter policies could yield better runtime guarantees. We consider two setups: one where the mutation rate follows a fixed schedule, and one where it may be adapted depending on the history of the run. For the first setup, we give a schedule that achieves a runtime of $(1\pm o(1))\beta n \ln n$, where $\beta \approx 3.552$, which is an asymptotic improvement over the runtime of the static setup. Moreover, we show that no schedule admits a better runtime guarantee and that the optimal schedule is essentially unique. For the second setup, we show that the runtime can be further improved to $(1\pm o(1)) e n \ln n$, which matches the performance of algorithms that know $n$ in advance. Finally, we study the related model of initial segment uncertainty with static position-dependent mutation rates, and derive asymptotically optimal lower bounds. This answers a question by Doerr, Doerr, and K\"otzing.

Approximating Real-Time Recurrent Learning with Random Kronecker Factors

Despite all the impressive advances of recurrent neural networks, sequential data is still in need of better modelling. Truncated backpropagation through time (TBPTT), the learning algorithm most widely used in practice, suffers from the truncation bias, which drastically limits its ability to learn long-term dependencies.The Real-Time Recurrent Learning algorithm (RTRL) addresses this issue, but its high computational requirements make it infeasible in practice. The Unbiased Online Recurrent Optimization algorithm (UORO) approximates RTRL with a smaller runtime and memory cost, but with the disadvantage of obtaining noisy gradients that also limit its practical applicability. In this paper we propose the Kronecker Factored RTRL (KF-RTRL) algorithm that uses a Kronecker product decomposition to approximate the gradients for a large class of RNNs. We show that KF-RTRL is an unbiased and memory efficient online learning algorithm. Our theoretical analysis shows that, under reasonable assumptions, the noise introduced by our algorithm is not only stable over time but also asymptotically much smaller than the one of the UORO algorithm. We also confirm these theoretical results experimentally. Further, we show empirically that the KF-RTRL algorithm captures long-term dependencies and almost matches the performance of TBPTT on real world tasks by training Recurrent Highway Networks on a synthetic string memorization task and on the Penn TreeBank task, respectively. These results indicate that RTRL based approaches might be a promising future alternative to TBPTT.

Fast-Slow Recurrent Neural Networks

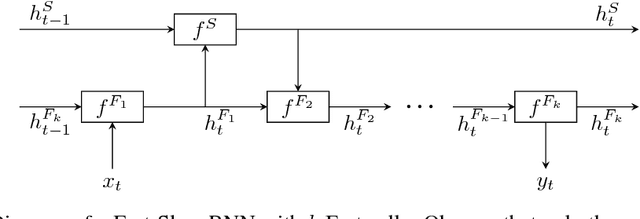
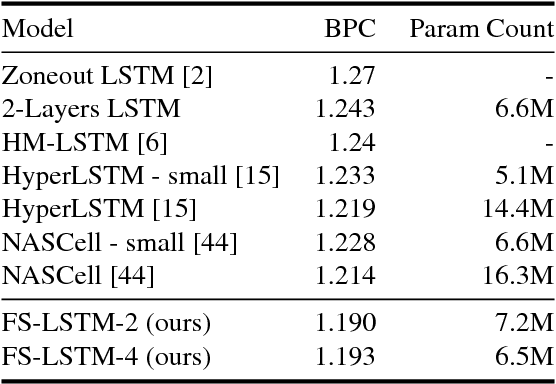
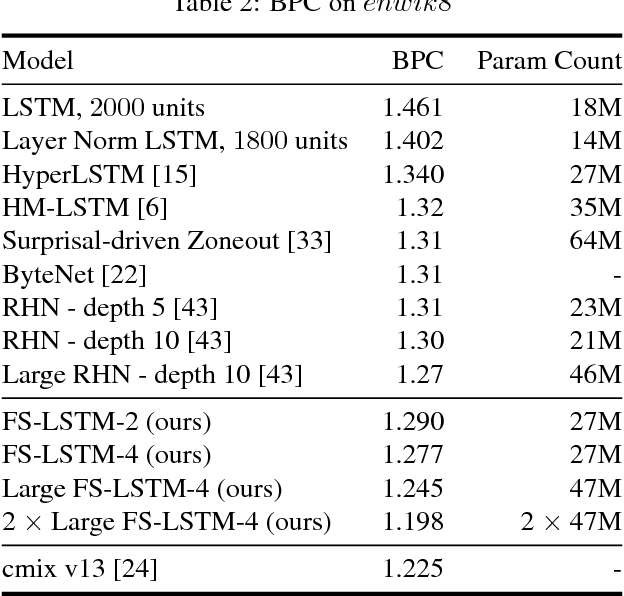
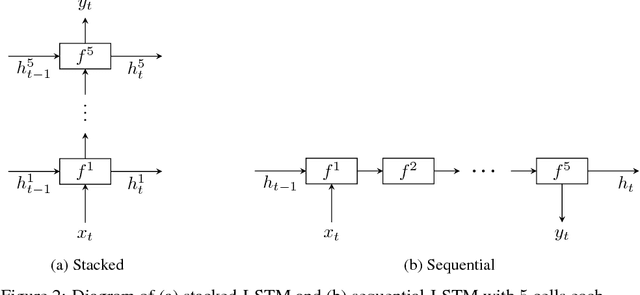
Processing sequential data of variable length is a major challenge in a wide range of applications, such as speech recognition, language modeling, generative image modeling and machine translation. Here, we address this challenge by proposing a novel recurrent neural network (RNN) architecture, the Fast-Slow RNN (FS-RNN). The FS-RNN incorporates the strengths of both multiscale RNNs and deep transition RNNs as it processes sequential data on different timescales and learns complex transition functions from one time step to the next. We evaluate the FS-RNN on two character level language modeling data sets, Penn Treebank and Hutter Prize Wikipedia, where we improve state of the art results to $1.19$ and $1.25$ bits-per-character (BPC), respectively. In addition, an ensemble of two FS-RNNs achieves $1.20$ BPC on Hutter Prize Wikipedia outperforming the best known compression algorithm with respect to the BPC measure. We also present an empirical investigation of the learning and network dynamics of the FS-RNN, which explains the improved performance compared to other RNN architectures. Our approach is general as any kind of RNN cell is a possible building block for the FS-RNN architecture, and thus can be flexibly applied to different tasks.