Towards an AI co-scientist

Scientific discovery relies on scientists generating novel hypotheses that undergo rigorous experimental validation. To augment this process, we introduce an AI co-scientist, a multi-agent system built on Gemini 2.0. The AI co-scientist is intended to help uncover new, original knowledge and to formulate demonstrably novel research hypotheses and proposals, building upon prior evidence and aligned to scientist-provided research objectives and guidance. The system's design incorporates a generate, debate, and evolve approach to hypothesis generation, inspired by the scientific method and accelerated by scaling test-time compute. Key contributions include: (1) a multi-agent architecture with an asynchronous task execution framework for flexible compute scaling; (2) a tournament evolution process for self-improving hypotheses generation. Automated evaluations show continued benefits of test-time compute, improving hypothesis quality. While general purpose, we focus development and validation in three biomedical areas: drug repurposing, novel target discovery, and explaining mechanisms of bacterial evolution and anti-microbial resistance. For drug repurposing, the system proposes candidates with promising validation findings, including candidates for acute myeloid leukemia that show tumor inhibition in vitro at clinically applicable concentrations. For novel target discovery, the AI co-scientist proposed new epigenetic targets for liver fibrosis, validated by anti-fibrotic activity and liver cell regeneration in human hepatic organoids. Finally, the AI co-scientist recapitulated unpublished experimental results via a parallel in silico discovery of a novel gene transfer mechanism in bacterial evolution. These results, detailed in separate, co-timed reports, demonstrate the potential to augment biomedical and scientific discovery and usher an era of AI empowered scientists.

Replacing Human Audio with Synthetic Audio for On-device Unspoken Punctuation Prediction

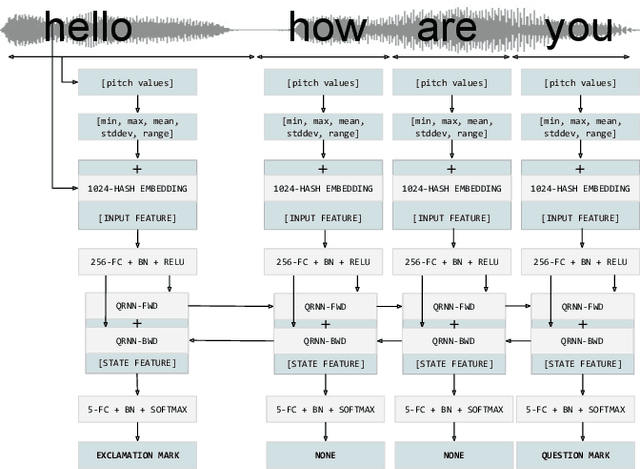
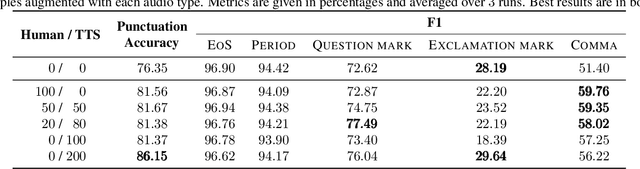
We present a novel multi-modal unspoken punctuation prediction system for the English language which combines acoustic and text features. We demonstrate for the first time, that by relying exclusively on synthetic data generated using a prosody-aware text-to-speech system, we can outperform a model trained with expensive human audio recordings on the unspoken punctuation prediction problem. Our model architecture is well suited for on-device use. This is achieved by leveraging hash-based embeddings of automatic speech recognition text output in conjunction with acoustic features as input to a quasi-recurrent neural network, keeping the model size small and latency low.

Decoupling Hierarchical Recurrent Neural Networks With Locally Computable Losses

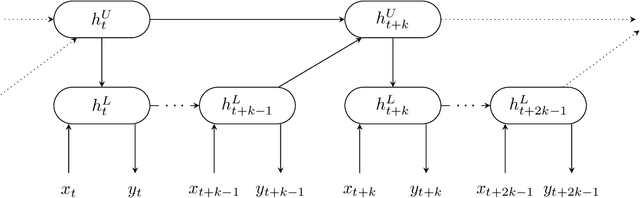
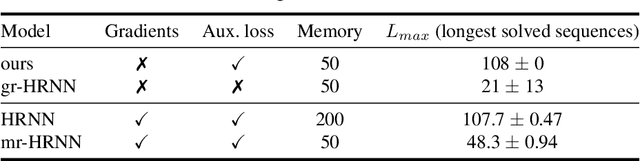
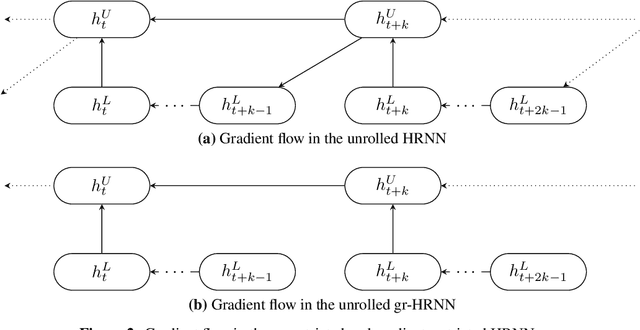
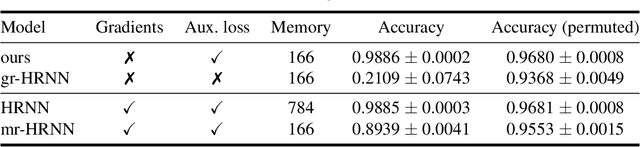
Learning long-term dependencies is a key long-standing challenge of recurrent neural networks (RNNs). Hierarchical recurrent neural networks (HRNNs) have been considered a promising approach as long-term dependencies are resolved through shortcuts up and down the hierarchy. Yet, the memory requirements of Truncated Backpropagation Through Time (TBPTT) still prevent training them on very long sequences. In this paper, we empirically show that in (deep) HRNNs, propagating gradients back from higher to lower levels can be replaced by locally computable losses, without harming the learning capability of the network, over a wide range of tasks. This decoupling by local losses reduces the memory requirements of training by a factor exponential in the depth of the hierarchy in comparison to standard TBPTT.

The linear hidden subset problem for the EA with scheduled and adaptive mutation rates

We study unbiased $(1+1)$ evolutionary algorithms on linear functions with an unknown number $n$ of bits with non-zero weight. Static algorithms achieve an optimal runtime of $O(n (\ln n)^{2+\epsilon})$, however, it remained unclear whether more dynamic parameter policies could yield better runtime guarantees. We consider two setups: one where the mutation rate follows a fixed schedule, and one where it may be adapted depending on the history of the run. For the first setup, we give a schedule that achieves a runtime of $(1\pm o(1))\beta n \ln n$, where $\beta \approx 3.552$, which is an asymptotic improvement over the runtime of the static setup. Moreover, we show that no schedule admits a better runtime guarantee and that the optimal schedule is essentially unique. For the second setup, we show that the runtime can be further improved to $(1\pm o(1)) e n \ln n$, which matches the performance of algorithms that know $n$ in advance. Finally, we study the related model of initial segment uncertainty with static position-dependent mutation rates, and derive asymptotically optimal lower bounds. This answers a question by Doerr, Doerr, and K\"otzing.