Decoupling Hierarchical Recurrent Neural Networks With Locally Computable Losses
Paper and Code
Oct 11, 2019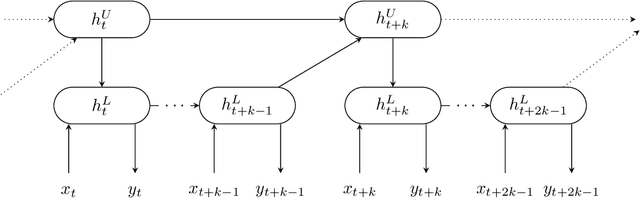
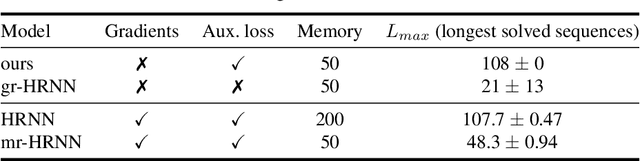
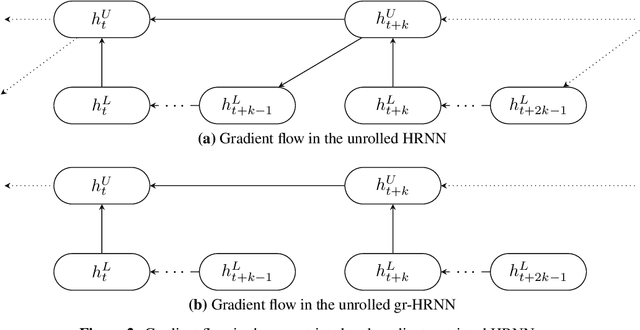
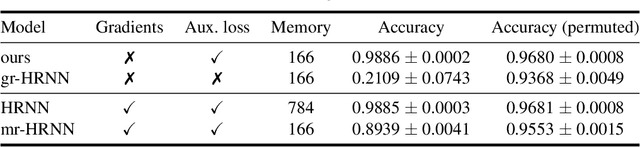
Learning long-term dependencies is a key long-standing challenge of recurrent neural networks (RNNs). Hierarchical recurrent neural networks (HRNNs) have been considered a promising approach as long-term dependencies are resolved through shortcuts up and down the hierarchy. Yet, the memory requirements of Truncated Backpropagation Through Time (TBPTT) still prevent training them on very long sequences. In this paper, we empirically show that in (deep) HRNNs, propagating gradients back from higher to lower levels can be replaced by locally computable losses, without harming the learning capability of the network, over a wide range of tasks. This decoupling by local losses reduces the memory requirements of training by a factor exponential in the depth of the hierarchy in comparison to standard TBPTT.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge