Humanity's Last Exam

Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.

Empirical Analysis of the Dynamic Binary Value Problem with IOHprofiler

Optimization problems in dynamic environments have recently been the source of several theoretical studies. One of these problems is the monotonic Dynamic Binary Value problem, which theoretically has high discriminatory power between different Genetic Algorithms. Given this theoretical foundation, we integrate several versions of this problem into the IOHprofiler benchmarking framework. Using this integration, we perform several large-scale benchmarking experiments to both recreate theoretical results on moderate dimensional problems and investigate aspects of GA's performance which have not yet been studied theoretically. Our results highlight some of the many synergies between theory and benchmarking and offer a platform through which further research into dynamic optimization problems can be performed.

How Population Diversity Influences the Efficiency of Crossover

Our theoretical understanding of crossover is limited by our ability to analyze how population diversity evolves. In this study, we provide one of the first rigorous analyses of population diversity and optimization time in a setting where large diversity and large population sizes are required to speed up progress. We give a formal and general criterion which amount of diversity is necessary and sufficient to speed up the $(\mu+1)$ Genetic Algorithm on LeadingOnes. We show that the naturally evolving diversity falls short of giving a substantial speed-up for any $\mu=O(\sqrt{n}/\log^2 n)$. On the other hand, we show that even for $\mu=2$, if we simply break ties in favor of diversity then this increases diversity so much that optimization is accelerated by a constant factor.

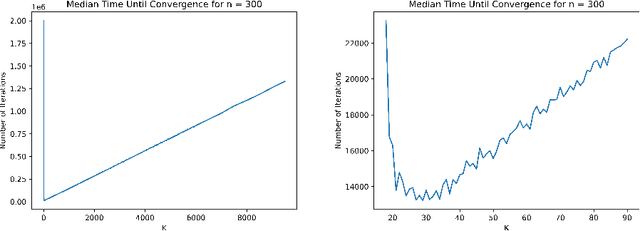
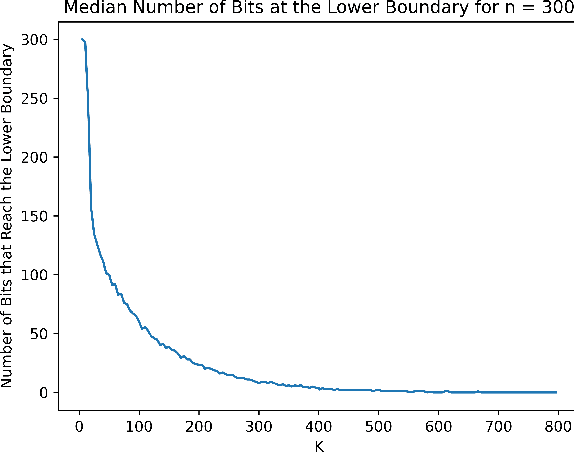
Faster Optimization Through Genetic Drift

The compact Genetic Algorithm (cGA), parameterized by its hypothetical population size $K$, offers a low-memory alternative to evolving a large offspring population of solutions. It evolves a probability distribution, biasing it towards promising samples. For the classical benchmark OneMax, the cGA has to two different modes of operation: a conservative one with small step sizes $\Theta(1/(\sqrt{n}\log n))$, which is slow but prevents genetic drift, and an aggressive one with large step sizes $\Theta(1/\log n)$, in which genetic drift leads to wrong decisions, but those are corrected efficiently. On OneMax, an easy hill-climbing problem, both modes lead to optimization times of $\Theta(n\log n)$ and are thus equally efficient. In this paper we study how both regimes change when we replace OneMax by the harder hill-climbing problem DynamicBinVal. It turns out that the aggressive mode is not affected and still yields quasi-linear runtime $O(n\cdot polylog (n))$. However, the conservative mode becomes substantially slower, yielding a runtime of $\Omega(n^2)$, since genetic drift can only be avoided with smaller step sizes of $O(1/n)$. We complement our theoretical results with simulations.

Self-Adjusting Evolutionary Algorithms Are Slow on Multimodal Landscapes

The one-fifth rule and its generalizations are a classical parameter control mechanism in discrete domains. They have also been transferred to control the offspring population size of the $(1, \lambda)$-EA. This has been shown to work very well for hill-climbing, and combined with a restart mechanism it was recently shown by Hevia Fajardo and Sudholt to improve performance on the multi-modal problem Cliff drastically. In this work we show that the positive results do not extend to other types of local optima. On the distorted OneMax benchmark, the self-adjusting $(1, \lambda)$-EA is slowed down just as elitist algorithms because self-adaptation prevents the algorithm from escaping from local optima. This makes the self-adaptive algorithm considerably worse than good static parameter choices, which do allow to escape from local optima efficiently. We show this theoretically and complement the result with empirical runtime results.

Plus Strategies are Exponentially Slower for Planted Optima of Random Height

We compare the $(1,\lambda)$-EA and the $(1 + \lambda)$-EA on the recently introduced benchmark DisOM, which is the OneMax function with randomly planted local optima. Previous work showed that if all local optima have the same relative height, then the plus strategy never loses more than a factor $O(n\log n)$ compared to the comma strategy. Here we show that even small random fluctuations in the heights of the local optima have a devastating effect for the plus strategy and lead to super-polynomial runtimes. On the other hand, due to their ability to escape local optima, comma strategies are unaffected by the height of the local optima and remain efficient. Our results hold for a broad class of possible distortions and show that the plus strategy, but not the comma strategy, is generally deceived by sparse unstructured fluctuations of a smooth landscape.

A Tight $O$ Runtime Bound for a GA on Jump$_k$ for Realistic Crossover Probabilities

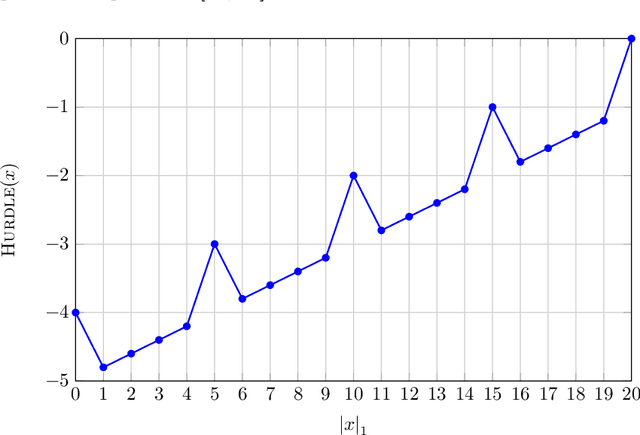
The Jump$_k$ benchmark was the first problem for which crossover was proven to give a speedup over mutation-only evolutionary algorithms. Jansen and Wegener (2002) proved an upper bound of $O({\rm poly}(n) + 4^k/p_c)$ for the ($\mu$+1)~Genetic Algorithm ($(\mu+1)$ GA), but only for unrealistically small crossover probabilities $p_c$. To this date, it remains an open problem to prove similar upper bounds for realistic~$p_c$; the best known runtime bound for $p_c = \Omega(1)$ is $O((n/\chi)^{k-1})$, $\chi$ a positive constant. Using recently developed techniques, we analyse the evolution of the population diversity, measured as sum of pairwise Hamming distances, for a variant of the \muga on Jump$_k$. We show that population diversity converges to an equilibrium of near-perfect diversity. This yields an improved and tight time bound of $O(\mu n \log(k) + 4^k/p_c)$ for a range of~$k$ under the mild assumptions $p_c = O(1/k)$ and $\mu \in \Omega(kn)$. For all constant~$k$ the restriction is satisfied for some $p_c = \Omega(1)$. Our work partially solves a problem that has been open for more than 20 years.

Hardest Monotone Functions for Evolutionary Algorithms

The study of hardest and easiest fitness landscapes is an active area of research. Recently, Kaufmann, Larcher, Lengler and Zou conjectured that for the self-adjusting $(1,\lambda)$-EA, Adversarial Dynamic BinVal (ADBV) is the hardest dynamic monotone function to optimize. We introduce the function Switching Dynamic BinVal (SDBV) which coincides with ADBV whenever the number of remaining zeros in the search point is strictly less than $n/2$, where $n$ denotes the dimension of the search space. We show, using a combinatorial argument, that for the $(1+1)$-EA with any mutation rate $p \in [0,1]$, SDBV is drift-minimizing among the class of dynamic monotone functions. Our construction provides the first explicit example of an instance of the partially-ordered evolutionary algorithm (PO-EA) model with parameterized pessimism introduced by Colin, Doerr and F\'erey, building on work of Jansen. We further show that the $(1+1)$-EA optimizes SDBV in $\Theta(n^{3/2})$ generations. Our simulations demonstrate matching runtimes for both static and self-adjusting $(1,\lambda)$ and $(1+\lambda)$-EA. We further show, using an example of fixed dimension, that drift-minimization does not equal maximal runtime.

Comma Selection Outperforms Plus Selection on OneMax with Randomly Planted Optima

It is an ongoing debate whether and how comma selection in evolutionary algorithms helps to escape local optima. We propose a new benchmark function to investigate the benefits of comma selection: OneMax with randomly planted local optima, generated by frozen noise. We show that comma selection (the $(1,\lambda)$ EA) is faster than plus selection (the $(1+\lambda)$ EA) on this benchmark, in a fixed-target scenario, and for offspring population sizes $\lambda$ for which both algorithms behave differently. For certain parameters, the $(1,\lambda)$ EA finds the target in $\Theta(n \ln n)$ evaluations, with high probability (w.h.p.), while the $(1+\lambda)$ EA) w.h.p. requires almost $\Theta((n\ln n)^2)$ evaluations. We further show that the advantage of comma selection is not arbitrarily large: w.h.p. comma selection outperforms plus selection at most by a factor of $O(n \ln n)$ for most reasonable parameter choices. We develop novel methods for analysing frozen noise and give powerful and general fixed-target results with tail bounds that are of independent interest.

Analysing Equilibrium States for Population Diversity

Population diversity is crucial in evolutionary algorithms as it helps with global exploration and facilitates the use of crossover. Despite many runtime analyses showing advantages of population diversity, we have no clear picture of how diversity evolves over time. We study how population diversity of $(\mu+1)$ algorithms, measured by the sum of pairwise Hamming distances, evolves in a fitness-neutral environment. We give an exact formula for the drift of population diversity and show that it is driven towards an equilibrium state. Moreover, we bound the expected time for getting close to the equilibrium state. We find that these dynamics, including the location of the equilibrium, are unaffected by surprisingly many algorithmic choices. All unbiased mutation operators with the same expected number of bit flips have the same effect on the expected diversity. Many crossover operators have no effect at all, including all binary unbiased, respectful operators. We review crossover operators from the literature and identify crossovers that are neutral towards the evolution of diversity and crossovers that are not.