Andre Opris
Towards a Rigorous Understanding of the Population Dynamics of the NSGA-III: Tight Runtime Bounds
Nov 10, 2025Abstract:Evolutionary algorithms are widely used for solving multi-objective optimization problems. A prominent example is NSGA-III, which is particularly well suited for solving problems involving more than three objectives, distinguishing it from the classical NSGA-II. Despite its empirical success, the theoretical understanding of NSGA III remains very limited, especially with respect to runtime analysis. A central open problem concerns its population dynamics, which involve controlling the maximum number of individuals sharing the same fitness value during the exploration process. In this paper, we make a significant step towards such an understanding by proving tight runtime bounds for NSGA-III on the bi-objective OneMinMax ($2$-OMM) problem. Firstly, we prove that NSGA-III requires $Ω(n^2 \log(n) / μ)$ generations in expectation to optimize $2$-OMM assuming the population size $μ$ satisfies $n+1 \leq μ=O(\log(n)^c(n+1))$ where $n$ denotes the problem size and $c<1$ is a constant. Apart from~\cite{opris2025multimodal}, this is the first proven lower runtime bound for NSGA-III on a classical benchmark problem. Complementing this, we secondly improve the best known upper bound of NSGA-III on the $m$-objective OneMinMax problem ($m$-OMM) of $O(n \log(n))$ generations by a factor of $μ/(2n/m + 1)^{m/2}$ for a constant number $m$ of objectives and population size $(2n/m + 1)^{m/2} \leq μ\in O(\sqrt{\log(n)} (2n/m + 1)^{m/2})$. This yields tight runtime bounds in the case $m = 2$, and the surprising result that NSGA-III beats NSGA-II by a factor of $μ/n$ in the expected runtime.
Tight Runtime Guarantees From Understanding the Population Dynamics of the GSEMO Multi-Objective Evolutionary Algorithm
May 02, 2025Abstract:The global simple evolutionary multi-objective optimizer (GSEMO) is a simple, yet often effective multi-objective evolutionary algorithm (MOEA). By only maintaining non-dominated solutions, it has a variable population size that automatically adjusts to the needs of the optimization process. The downside of the dynamic population size is that the population dynamics of this algorithm are harder to understand, resulting, e.g., in the fact that only sporadic tight runtime analyses exist. In this work, we significantly enhance our understanding of the dynamics of the GSEMO, in particular, for the classic CountingOnesCountingZeros (COCZ) benchmark. From this, we prove a lower bound of order $\Omega(n^2 \log n)$, for the first time matching the seminal upper bounds known for over twenty years. We also show that the GSEMO finds any constant fraction of the Pareto front in time $O(n^2)$, improving over the previous estimate of $O(n^2 \log n)$ for the time to find the first Pareto optimum. Our methods extend to other classic benchmarks and yield, e.g., the first $\Omega(n^{k+1})$ lower bound for the OJZJ benchmark in the case that the gap parameter is $k \in \{2,3\}$. We are therefore optimistic that our new methods will be useful in future mathematical analyses of MOEAs.
A First Runtime Analysis of NSGA-III on a Many-Objective Multimodal Problem: Provable Exponential Speedup via Stochastic Population Update
May 02, 2025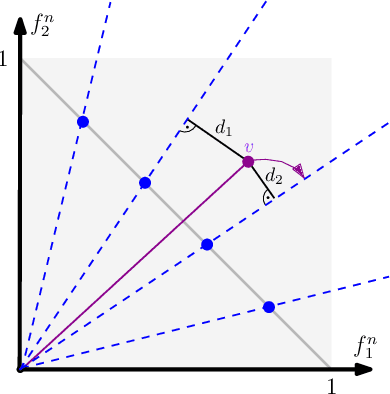
Abstract:The NSGA-III is a prominent algorithm in evolutionary many-objective optimization. It is well-suited for optimizing functions with more than three objectives, setting it apart from the classic NSGA-II. However, theoretical insights about NSGA-III of when and why it performs well are still in its early development. This paper addresses this point and conducts a rigorous runtime analysis of NSGA-III on the many-objective \textsc{OneJumpZeroJump} benchmark (\textsc{OjZj} for short), providing the first runtime bounds where the number of objectives is constant. We show that NSGA-III finds the Pareto front of \textsc{OjZj} in time $O(n^{k+d/2}+ \mu n \ln(n))$ where $n$ is the problem size, $d$ is the number of objectives, $k$ is the gap size, a problem specific parameter, if its population size $\mu \in 2^{O(n)}$ is at least $(2n/d+1)^{d/2}$. Notably, NSGA-III is faster than NSGA-II by a factor of $\mu/n^{d/2}$ for some $\mu \in \omega(n^{d/2})$. We also show that a stochastic population update, proposed by Bian et al., provably guarantees a speedup of order $\Theta((k/b)^{k-1})$ in the runtime where $b>0$ is a constant. To our knowledge, this is the first rigorous runtime analysis of NSGA-III on \textsc{OjZj}. Proving these bounds requires a much deeper understanding of the population dynamics of NSGA-III than previous papers achieved.
A Many Objective Problem Where Crossover is Provably Indispensable
Dec 24, 2024
Abstract:This paper addresses theory in evolutionary multiobjective optimisation (EMO) and focuses on the role of crossover operators in many-objective optimisation. The advantages of using crossover are hardly understood and rigorous runtime analyses with crossover are lagging far behind its use in practice, specifically in the case of more than two objectives. We present a many-objective problem class together with a theoretical runtime analysis of the widely used NSGA-III to demonstrate that crossover can yield an exponential speedup on the runtime. In particular, this algorithm can find the Pareto set in expected polynomial time when using crossover while without crossover it requires exponential time to even find a single Pareto-optimal point. To our knowledge, this is the first rigorous runtime analysis in many-objective optimisation demonstrating an exponential performance gap when using crossover for more than two objectives.
Theoretical Analysis of Quality Diversity Algorithms for a Classical Path Planning Problem
Dec 16, 2024
Abstract:Quality diversity (QD) algorithms have shown to provide sets of high quality solutions for challenging problems in robotics, games, and combinatorial optimisation. So far, theoretical foundational explaining their good behaviour in practice lack far behind their practical success. We contribute to the theoretical understanding of these algorithms and study the behaviour of QD algorithms for a classical planning problem seeking several solutions. We study the all-pairs-shortest-paths (APSP) problem which gives a natural formulation of the behavioural space based on all pairs of nodes of the given input graph that can be used by Map-Elites QD algorithms. Our results show that Map-Elites QD algorithms are able to compute a shortest path for each pair of nodes efficiently in parallel. Furthermore, we examine parent selection techniques for crossover that exhibit significant speed ups compared to the standard QD approach.
Illustrating the Efficiency of Popular Evolutionary Multi-Objective Algorithms Using Runtime Analysis
May 22, 2024
Abstract:Runtime analysis has recently been applied to popular evolutionary multi-objective (EMO) algorithms like NSGA-II in order to establish a rigorous theoretical foundation. However, most analyses showed that these algorithms have the same performance guarantee as the simple (G)SEMO algorithm. To our knowledge, there are no runtime analyses showing an advantage of a popular EMO algorithm over the simple algorithm for deterministic problems. We propose such a problem and use it to showcase the superiority of popular EMO algorithms over (G)SEMO: OneTrapZeroTrap is a straightforward generalization of the well-known Trap function to two objectives. We prove that, while GSEMO requires at least $n^n$ expected fitness evaluations to optimise OneTrapZeroTrap, popular EMO algorithms NSGA-II, NSGA-III and SMS-EMOA, all enhanced with a mild diversity mechanism of avoiding genotype duplication, only require $O(n \log n)$ expected fitness evaluations. Our analysis reveals the importance of the key components in each of these sophisticated algorithms and contributes to a better understanding of their capabilities.
Runtime Analyses of NSGA-III on Many-Objective Problems
Apr 18, 2024Abstract:NSGA-II and NSGA-III are two of the most popular evolutionary multi-objective algorithms used in practice. While NSGA-II is used for few objectives such as 2 and 3, NSGA-III is designed to deal with a larger number of objectives. In a recent breakthrough, Wietheger and Doerr (IJCAI 2023) gave the first runtime analysis for NSGA-III on the 3-objective OneMinMax problem, showing that this state-of-the-art algorithm can be analyzed rigorously. We advance this new line of research by presenting the first runtime analyses of NSGA-III on the popular many-objective benchmark problems mLOTZ, mOMM, and mCOCZ, for an arbitrary constant number $m$ of objectives. Our analysis provides ways to set the important parameters of the algorithm: the number of reference points and the population size, so that a good performance can be guaranteed. We show how these parameters should be scaled with the problem dimension, the number of objectives and the fitness range. To our knowledge, these are the first runtime analyses for NSGA-III for more than 3 objectives.
A Tight $O$ Runtime Bound for a GA on Jump$_k$ for Realistic Crossover Probabilities
Apr 10, 2024
Abstract:The Jump$_k$ benchmark was the first problem for which crossover was proven to give a speedup over mutation-only evolutionary algorithms. Jansen and Wegener (2002) proved an upper bound of $O({\rm poly}(n) + 4^k/p_c)$ for the ($\mu$+1)~Genetic Algorithm ($(\mu+1)$ GA), but only for unrealistically small crossover probabilities $p_c$. To this date, it remains an open problem to prove similar upper bounds for realistic~$p_c$; the best known runtime bound for $p_c = \Omega(1)$ is $O((n/\chi)^{k-1})$, $\chi$ a positive constant. Using recently developed techniques, we analyse the evolution of the population diversity, measured as sum of pairwise Hamming distances, for a variant of the \muga on Jump$_k$. We show that population diversity converges to an equilibrium of near-perfect diversity. This yields an improved and tight time bound of $O(\mu n \log(k) + 4^k/p_c)$ for a range of~$k$ under the mild assumptions $p_c = O(1/k)$ and $\mu \in \Omega(kn)$. For all constant~$k$ the restriction is satisfied for some $p_c = \Omega(1)$. Our work partially solves a problem that has been open for more than 20 years.
Analysing the Robustness of NSGA-II under Noise
Jun 07, 2023Abstract:Runtime analysis has produced many results on the efficiency of simple evolutionary algorithms like the (1+1) EA, and its analogue called GSEMO in evolutionary multiobjective optimisation (EMO). Recently, the first runtime analyses of the famous and highly cited EMO algorithm NSGA-II have emerged, demonstrating that practical algorithms with thousands of applications can be rigorously analysed. However, these results only show that NSGA-II has the same performance guarantees as GSEMO and it is unclear how and when NSGA-II can outperform GSEMO. We study this question in noisy optimisation and consider a noise model that adds large amounts of posterior noise to all objectives with some constant probability $p$ per evaluation. We show that GSEMO fails badly on every noisy fitness function as it tends to remove large parts of the population indiscriminately. In contrast, NSGA-II is able to handle the noise efficiently on \textsc{LeadingOnesTrailingZeroes} when $p<1/2$, as the algorithm is able to preserve useful search points even in the presence of noise. We identify a phase transition at $p=1/2$ where the expected time to cover the Pareto front changes from polynomial to exponential. To our knowledge, this is the first proof that NSGA-II can outperform GSEMO and the first runtime analysis of NSGA-II in noisy optimisation.
Analysing Equilibrium States for Population Diversity
Apr 19, 2023Abstract:Population diversity is crucial in evolutionary algorithms as it helps with global exploration and facilitates the use of crossover. Despite many runtime analyses showing advantages of population diversity, we have no clear picture of how diversity evolves over time. We study how population diversity of $(\mu+1)$ algorithms, measured by the sum of pairwise Hamming distances, evolves in a fitness-neutral environment. We give an exact formula for the drift of population diversity and show that it is driven towards an equilibrium state. Moreover, we bound the expected time for getting close to the equilibrium state. We find that these dynamics, including the location of the equilibrium, are unaffected by surprisingly many algorithmic choices. All unbiased mutation operators with the same expected number of bit flips have the same effect on the expected diversity. Many crossover operators have no effect at all, including all binary unbiased, respectful operators. We review crossover operators from the literature and identify crossovers that are neutral towards the evolution of diversity and crossovers that are not.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge