Scalable Speed-ups for the SMS-EMOA from a Simple Aging Strategy

Different from single-objective evolutionary algorithms, where non-elitism is an established concept, multi-objective evolutionary algorithms almost always select the next population in a greedy fashion. In the only notable exception, Bian, Zhou, Li, and Qian (IJCAI 2023) proposed a stochastic selection mechanism for the SMS-EMOA and proved that it can speed up computing the Pareto front of the bi-objective jump benchmark with problem size $n$ and gap parameter $k$ by a factor of $\max\{1,2^{k/4}/n\}$. While this constitutes the first proven speed-up from non-elitist selection, suggesting a very interesting research direction, it has to be noted that a true speed-up only occurs for $k \ge 4\log_2(n)$, where the runtime is super-polynomial, and that the advantage reduces for larger numbers of objectives as shown in a later work. In this work, we propose a different non-elitist selection mechanism based on aging, which exempts individuals younger than a certain age from a possible removal. This remedies the two shortcomings of stochastic selection: We prove a speed-up by a factor of $\max\{1,\Theta(k)^{k-1}\}$, regardless of the number of objectives. In particular, a positive speed-up can already be observed for constant $k$, the only setting for which polynomial runtimes can be witnessed. Overall, this result supports the use of non-elitist selection schemes, but suggests that aging-based mechanisms can be considerably more powerful than stochastic selection mechanisms.

Proven Approximation Guarantees in Multi-Objective Optimization: SPEA2 Beats NSGA-II

Together with the NSGA-II and SMS-EMOA, the strength Pareto evolutionary algorithm 2 (SPEA2) is one of the most prominent dominance-based multi-objective evolutionary algorithms (MOEAs). Different from the NSGA-II, it does not employ the crowding distance (essentially the distance to neighboring solutions) to compare pairwise non-dominating solutions but a complex system of $\sigma$-distances that builds on the distances to all other solutions. In this work, we give a first mathematical proof showing that this more complex system of distances can be superior. More specifically, we prove that a simple steady-state SPEA2 can compute optimal approximations of the Pareto front of the OneMinMax benchmark in polynomial time. The best proven guarantee for a comparable variant of the NSGA-II only assures approximation ratios of roughly a factor of two, and both mathematical analyses and experiments indicate that optimal approximations are not found efficiently.

Tight Runtime Guarantees From Understanding the Population Dynamics of the GSEMO Multi-Objective Evolutionary Algorithm

The global simple evolutionary multi-objective optimizer (GSEMO) is a simple, yet often effective multi-objective evolutionary algorithm (MOEA). By only maintaining non-dominated solutions, it has a variable population size that automatically adjusts to the needs of the optimization process. The downside of the dynamic population size is that the population dynamics of this algorithm are harder to understand, resulting, e.g., in the fact that only sporadic tight runtime analyses exist. In this work, we significantly enhance our understanding of the dynamics of the GSEMO, in particular, for the classic CountingOnesCountingZeros (COCZ) benchmark. From this, we prove a lower bound of order $\Omega(n^2 \log n)$, for the first time matching the seminal upper bounds known for over twenty years. We also show that the GSEMO finds any constant fraction of the Pareto front in time $O(n^2)$, improving over the previous estimate of $O(n^2 \log n)$ for the time to find the first Pareto optimum. Our methods extend to other classic benchmarks and yield, e.g., the first $\Omega(n^{k+1})$ lower bound for the OJZJ benchmark in the case that the gap parameter is $k \in \{2,3\}$. We are therefore optimistic that our new methods will be useful in future mathematical analyses of MOEAs.

The First Theoretical Approximation Guarantees for the Non-Dominated Sorting Genetic Algorithm III (NSGA-III)

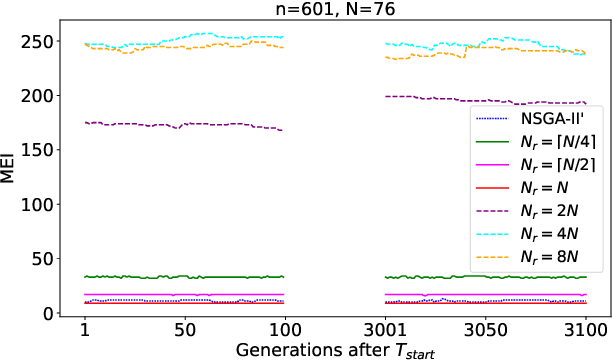
This work conducts a first theoretical analysis studying how well the NSGA-III approximates the Pareto front when the population size $N$ is less than the Pareto front size. We show that when $N$ is at least the number $N_r$ of reference points, then the approximation quality, measured by the maximum empty interval (MEI) indicator, on the OneMinMax benchmark is such that there is no empty interval longer than $\lceil\frac{(5-2\sqrt2)n}{N_r-1}\rceil$. This bound is independent of $N$, which suggests that further increasing the population size does not increase the quality of approximation when $N_r$ is fixed. This is a notable difference to the NSGA-II with sequential survival selection, where increasing the population size improves the quality of the approximations. We also prove two results indicating approximation difficulties when $N<N_r$. These theoretical results suggest that the best setting to approximate the Pareto front is $N_r=N$. In our experiments, we observe that with this setting the NSGA-III computes optimal approximations, very different from the NSGA-II, for which optimal approximations have not been observed so far.

Runtime Analysis of the Compact Genetic Algorithm on the LeadingOnes Benchmark

The compact genetic algorithm (cGA) is one of the simplest estimation-of-distribution algorithms (EDAs). Next to the univariate marginal distribution algorithm (UMDA) -- another simple EDA -- , the cGA has been subject to extensive mathematical runtime analyses, often showcasing a similar or even superior performance to competing approaches. Surprisingly though, up to date and in contrast to the UMDA and many other heuristics, we lack a rigorous runtime analysis of the cGA on the LeadingOnes benchmark -- one of the most studied theory benchmarks in the domain of evolutionary computation. We fill this gap in the literature by conducting a formal runtime analysis of the cGA on LeadingOnes. For the cGA's single parameter -- called the hypothetical population size -- at least polylogarithmically larger than the problem size, we prove that the cGA samples the optimum of LeadingOnes with high probability within a number of function evaluations quasi-linear in the problem size and linear in the hypothetical population size. For the best hypothetical population size, our result matches, up to polylogarithmic factors, the typical quadratic runtime that many randomized search heuristics exhibit on LeadingOnes. Our analysis exhibits some noteworthy differences in the working principles of the two algorithms which were not visible in previous works.

Runtime Analysis for Multi-Objective Evolutionary Algorithms in Unbounded Integer Spaces

Randomized search heuristics have been applied successfully to a plethora of problems. This success is complemented by a large body of theoretical results. Unfortunately, the vast majority of these results regard problems with binary or continuous decision variables -- the theoretical analysis of randomized search heuristics for unbounded integer domains is almost nonexistent. To resolve this shortcoming, we start the runtime analysis of multi-objective evolutionary algorithms, which are among the most successful randomized search heuristics, for unbounded integer search spaces. We analyze single- and full-dimensional mutation operators with three different mutation strengths, namely changes by plus/minus one (unit strength), random changes following a law with exponential tails, and random changes following a power-law. The performance guarantees we prove on a recently proposed natural benchmark problem suggest that unit mutation strengths can be slow when the initial solutions are far from the Pareto front. When setting the expected change right (depending on the benchmark parameter and the distance of the initial solutions), the mutation strength with exponential tails yields the best runtime guarantees in our results -- however, with a wrong choice of this expectation, the performance guarantees quickly become highly uninteresting. With power-law mutation, which is an essentially parameter-less mutation operator, we obtain good results uniformly over all problem parameters and starting points. We complement our mathematical findings with experimental results that suggest that our bounds are not always tight. Most prominently, our experiments indicate that power-law mutation outperforms the one with exponential tails even when the latter uses a near-optimal parametrization. Hence, we suggest to favor power-law mutation for unknown problems in integer spaces.

Speeding Up the NSGA-II With a Simple Tie-Breaking Rule

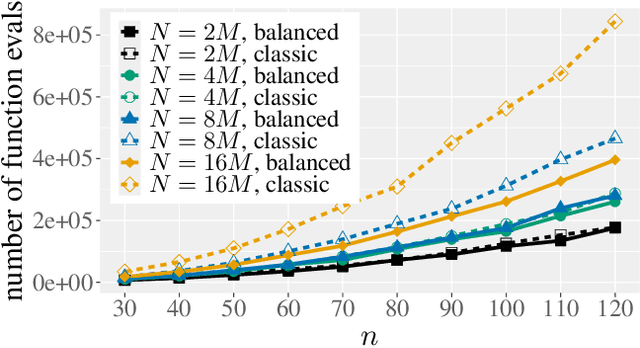
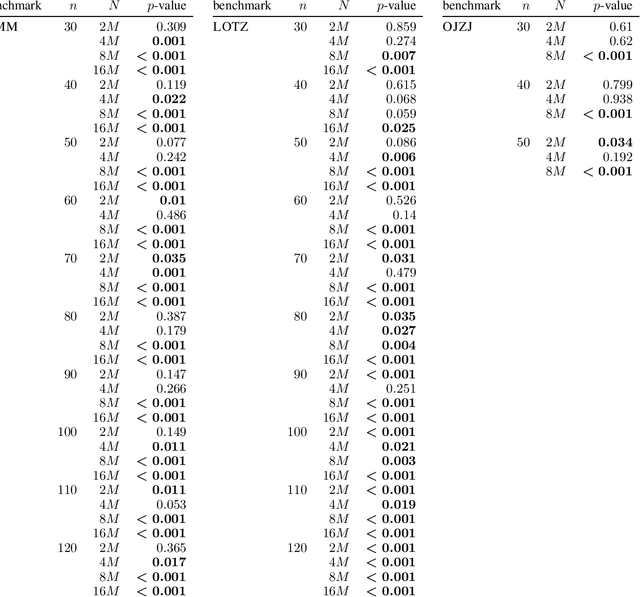
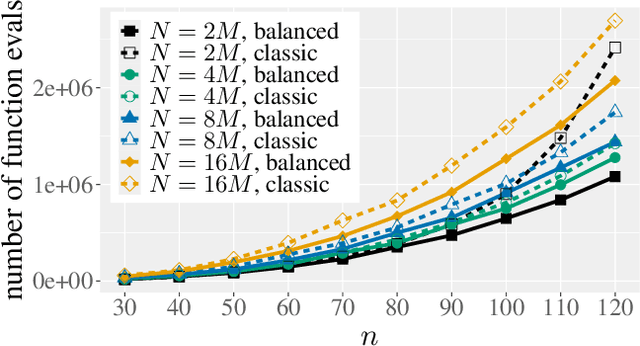
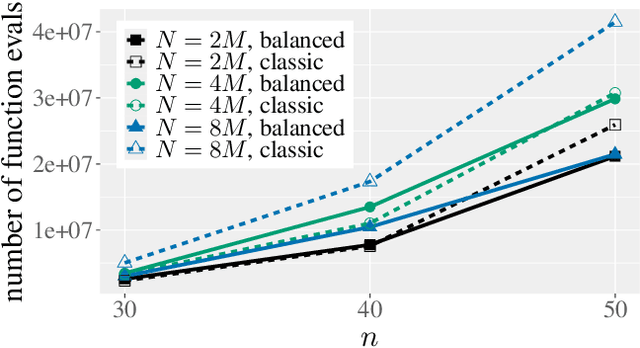
The non-dominated sorting genetic algorithm~II (NSGA-II) is the most popular multi-objective optimization heuristic. Recent mathematical runtime analyses have detected two shortcomings in discrete search spaces, namely, that the NSGA-II has difficulties with more than two objectives and that it is very sensitive to the choice of the population size. To overcome these difficulties, we analyze a simple tie-breaking rule in the selection of the next population. Similar rules have been proposed before, but have found only little acceptance. We prove the effectiveness of our tie-breaking rule via mathematical runtime analyses on the classic OneMinMax, LeadingOnesTrailingZeros, and OneJumpZeroJump benchmarks. We prove that this modified NSGA-II can optimize the three benchmarks efficiently also for many objectives, in contrast to the exponential lower runtime bound previously shown for OneMinMax with three or more objectives. For the bi-objective problems, we show runtime guarantees that do not increase when moderately increasing the population size over the minimum admissible size. For example, for the OneJumpZeroJump problem with representation length $n$ and gap parameter $k$, we show a runtime guarantee of $O(\max\{n^{k+1},Nn\})$ function evaluations when the population size is at least four times the size of the Pareto front. For population sizes larger than the minimal choice $N = \Theta(n)$, this result improves considerably over the $\Theta(Nn^k)$ runtime of the classic NSGA-II.

Difficulties of the NSGA-II with the Many-Objective LeadingOnes Problem

The NSGA-II is the most prominent multi-objective evolutionary algorithm (cited more than 50,000 times). Very recently, a mathematical runtime analysis has proven that this algorithm can have enormous difficulties when the number of objectives is larger than two (Zheng, Doerr. IEEE Transactions on Evolutionary Computation (2024)). However, this result was shown only for the OneMinMax benchmark problem, which has the particularity that all solutions are on the Pareto front, a fact heavily exploited in the proof of this result. In this work, we show a comparable result for the LeadingOnesTrailingZeroes benchmark. This popular benchmark problem appears more natural in that most of its solutions are not on the Pareto front. With a careful analysis of the population dynamics of the NGSA-II optimizing this benchmark, we manage to show that when the population grows on the Pareto front, then it does so much faster by creating known Pareto optima than by spreading out on the Pareto front. Consequently, already when still a constant fraction of the Pareto front is unexplored, the crowding distance becomes the crucial selection mechanism, and thus the same problems arise as in the optimization of OneMinMax. With these and some further arguments, we show that the NSGA-II, with a population size by at most a constant factor larger than the Pareto front, cannot compute the Pareto front in less than exponential time.

Evolutionary Algorithms Are Significantly More Robust to Noise When They Ignore It

Randomized search heuristics (RHSs) are generally believed to be robust to noise. However, almost all mathematical analyses on how RSHs cope with a noisy access to the objective function assume that each solution is re-evaluated whenever it is compared to others. This is unfortunate, both because it wastes computational resources and because it requires the user to foresee that noise is present (as in a noise-free setting, one would never re-evaluate solutions). In this work, we show the need for re-evaluations could be overestimated, and in fact, detrimental. For the classic benchmark problem of how the $(1+1)$ evolutionary algorithm optimizes the LeadingOnes benchmark, we show that without re-evaluations up to constant noise rates can be tolerated, much more than the $O(n^{-2} \log n)$ noise rates that can be tolerated when re-evaluating solutions. This first runtime analysis of an evolutionary algorithm solving a single-objective noisy problem without re-evaluations could indicate that such algorithms cope with noise much better than previously thought, and without the need to foresee the presence of noise.

Overcome the Difficulties of NSGA-II via Truthful Crowding Distance with Theoretical Guarantees

The NSGA-II is proven to encounter difficulties for more than two objectives, and the deduced reason is the crowding distance computed by regarding the different objectives independently. The recent theoretical efficiency of the NSGA-III and the SMS-EMOA also supports the deduced reason as both algorithms consider the dependencies of objectives in the second criterion after the non-dominated sorting but with complicated structure or difficult computation. However, there is still a question of whether a simple modification of the original crowding distance can help. This paper proposes such a variant, called truthful crowding distance. This variant inherits the simple structure of summing the component for each objective. For each objective, it first sorts the set of solutions in order of descending objective values, and uses the smallest normalized L1 distance between the current solution and solutions in the earlier positions of the sorted list as the component. Summing up all components gives the value of truthful crowding distance. We call this NSGA-II variant by NSGA-II-T that replaces the original crowding distance with the truthful one, and that sequentially updates the crowding distance value after each removal. We prove that the NSGA-II-T can efficiently cover the full Pareto front for many-objective mOneMinMax and mOJZJ, in contrast to the exponential runtime of the original NSGA-II. Besides, we also prove that it theoretically achieves a slightly better approximation of the Pareto front for OneMinMax than the original NSGA-II with sequential survival selection. Besides, it is the first NSGA-II variant with a simple structure that performs well for many objectives with theoretical guarantees.