Evolutionary Algorithms Are Significantly More Robust to Noise When They Ignore It
Paper and Code
Aug 31, 2024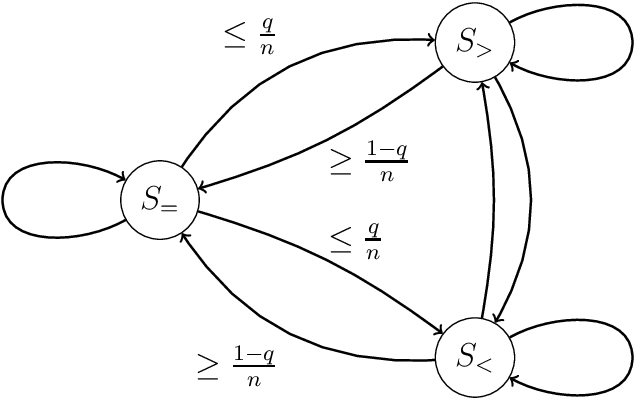



Randomized search heuristics (RHSs) are generally believed to be robust to noise. However, almost all mathematical analyses on how RSHs cope with a noisy access to the objective function assume that each solution is re-evaluated whenever it is compared to others. This is unfortunate, both because it wastes computational resources and because it requires the user to foresee that noise is present (as in a noise-free setting, one would never re-evaluate solutions). In this work, we show the need for re-evaluations could be overestimated, and in fact, detrimental. For the classic benchmark problem of how the $(1+1)$ evolutionary algorithm optimizes the LeadingOnes benchmark, we show that without re-evaluations up to constant noise rates can be tolerated, much more than the $O(n^{-2} \log n)$ noise rates that can be tolerated when re-evaluating solutions. This first runtime analysis of an evolutionary algorithm solving a single-objective noisy problem without re-evaluations could indicate that such algorithms cope with noise much better than previously thought, and without the need to foresee the presence of noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge