Weijie Zheng
Scalable Speed-ups for the SMS-EMOA from a Simple Aging Strategy
May 03, 2025Abstract:Different from single-objective evolutionary algorithms, where non-elitism is an established concept, multi-objective evolutionary algorithms almost always select the next population in a greedy fashion. In the only notable exception, Bian, Zhou, Li, and Qian (IJCAI 2023) proposed a stochastic selection mechanism for the SMS-EMOA and proved that it can speed up computing the Pareto front of the bi-objective jump benchmark with problem size $n$ and gap parameter $k$ by a factor of $\max\{1,2^{k/4}/n\}$. While this constitutes the first proven speed-up from non-elitist selection, suggesting a very interesting research direction, it has to be noted that a true speed-up only occurs for $k \ge 4\log_2(n)$, where the runtime is super-polynomial, and that the advantage reduces for larger numbers of objectives as shown in a later work. In this work, we propose a different non-elitist selection mechanism based on aging, which exempts individuals younger than a certain age from a possible removal. This remedies the two shortcomings of stochastic selection: We prove a speed-up by a factor of $\max\{1,\Theta(k)^{k-1}\}$, regardless of the number of objectives. In particular, a positive speed-up can already be observed for constant $k$, the only setting for which polynomial runtimes can be witnessed. Overall, this result supports the use of non-elitist selection schemes, but suggests that aging-based mechanisms can be considerably more powerful than stochastic selection mechanisms.
The First Theoretical Approximation Guarantees for the Non-Dominated Sorting Genetic Algorithm III (NSGA-III)
Apr 30, 2025

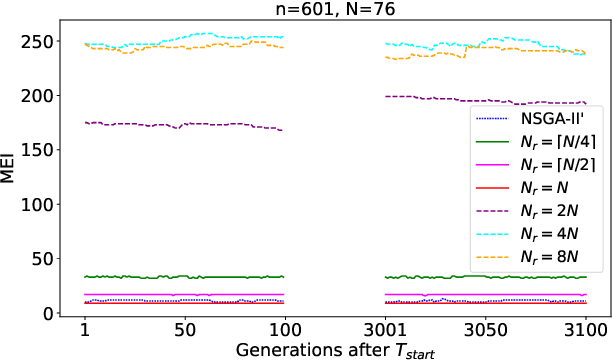

Abstract:This work conducts a first theoretical analysis studying how well the NSGA-III approximates the Pareto front when the population size $N$ is less than the Pareto front size. We show that when $N$ is at least the number $N_r$ of reference points, then the approximation quality, measured by the maximum empty interval (MEI) indicator, on the OneMinMax benchmark is such that there is no empty interval longer than $\lceil\frac{(5-2\sqrt2)n}{N_r-1}\rceil$. This bound is independent of $N$, which suggests that further increasing the population size does not increase the quality of approximation when $N_r$ is fixed. This is a notable difference to the NSGA-II with sequential survival selection, where increasing the population size improves the quality of the approximations. We also prove two results indicating approximation difficulties when $N<N_r$. These theoretical results suggest that the best setting to approximate the Pareto front is $N_r=N$. In our experiments, we observe that with this setting the NSGA-III computes optimal approximations, very different from the NSGA-II, for which optimal approximations have not been observed so far.
Towards Million-Scale Adversarial Robustness Evaluation With Stronger Individual Attacks
Nov 20, 2024



Abstract:As deep learning models are increasingly deployed in safety-critical applications, evaluating their vulnerabilities to adversarial perturbations is essential for ensuring their reliability and trustworthiness. Over the past decade, a large number of white-box adversarial robustness evaluation methods (i.e., attacks) have been proposed, ranging from single-step to multi-step methods and from individual to ensemble methods. Despite these advances, challenges remain in conducting meaningful and comprehensive robustness evaluations, particularly when it comes to large-scale testing and ensuring evaluations reflect real-world adversarial risks. In this work, we focus on image classification models and propose a novel individual attack method, Probability Margin Attack (PMA), which defines the adversarial margin in the probability space rather than the logits space. We analyze the relationship between PMA and existing cross-entropy or logits-margin-based attacks, and show that PMA can outperform the current state-of-the-art individual methods. Building on PMA, we propose two types of ensemble attacks that balance effectiveness and efficiency. Furthermore, we create a million-scale dataset, CC1M, derived from the existing CC3M dataset, and use it to conduct the first million-scale white-box adversarial robustness evaluation of adversarially-trained ImageNet models. Our findings provide valuable insights into the robustness gaps between individual versus ensemble attacks and small-scale versus million-scale evaluations.
Theoretical Advantage of Multiobjective Evolutionary Algorithms for Problems with Different Degrees of Conflict
Aug 08, 2024Abstract:The field of multiobjective evolutionary algorithms (MOEAs) often emphasizes its popularity for optimization problems with conflicting objectives. However, it is still theoretically unknown how MOEAs perform for different degrees of conflict, even for no conflicts, compared with typical approaches outside this field. As the first step to tackle this question, we propose the OneMaxMin$_k$ benchmark class with the degree of the conflict $k\in[0..n]$, a generalized variant of COCZ and OneMinMax. Two typical non-MOEA approaches, scalarization (weighted-sum approach) and $\epsilon$-constraint approach, are considered. We prove that for any set of weights, the set of optima found by scalarization approach cannot cover the full Pareto front. Although the set of the optima of constrained problems constructed via $\epsilon$-constraint approach can cover the full Pareto front, the general used ways (via exterior or nonparameter penalty functions) to solve such constrained problems encountered difficulties. The nonparameter penalty function way cannot construct the set of optima whose function values are the Pareto front, and the exterior way helps (with expected runtime of $O(n\ln n)$ for the randomized local search algorithm for reaching any Pareto front point) but with careful settings of $\epsilon$ and $r$ ($r>1/(\epsilon+1-\lceil \epsilon \rceil)$). In constrast, the generally analyzed MOEAs can efficiently solve OneMaxMin$_k$ without above careful designs. We prove that (G)SEMO, MOEA/D, NSGA-II, and SMS-EMOA can cover the full Pareto front in $O(\max\{k,1\}n\ln n)$ expected number of function evaluations, which is the same asymptotic runtime as the exterior way in $\epsilon$-constraint approach with careful settings. As a side result, our results also give the performance analysis of solving a constrained problem via multiobjective way.
Downstream Transfer Attack: Adversarial Attacks on Downstream Models with Pre-trained Vision Transformers
Aug 03, 2024



Abstract:With the advancement of vision transformers (ViTs) and self-supervised learning (SSL) techniques, pre-trained large ViTs have become the new foundation models for computer vision applications. However, studies have shown that, like convolutional neural networks (CNNs), ViTs are also susceptible to adversarial attacks, where subtle perturbations in the input can fool the model into making false predictions. This paper studies the transferability of such an adversarial vulnerability from a pre-trained ViT model to downstream tasks. We focus on \emph{sample-wise} transfer attacks and propose a novel attack method termed \emph{Downstream Transfer Attack (DTA)}. For a given test image, DTA leverages a pre-trained ViT model to craft the adversarial example and then applies the adversarial example to attack a fine-tuned version of the model on a downstream dataset. During the attack, DTA identifies and exploits the most vulnerable layers of the pre-trained model guided by a cosine similarity loss to craft highly transferable attacks. Through extensive experiments with pre-trained ViTs by 3 distinct pre-training methods, 3 fine-tuning schemes, and across 10 diverse downstream datasets, we show that DTA achieves an average attack success rate (ASR) exceeding 90\%, surpassing existing methods by a huge margin. When used with adversarial training, the adversarial examples generated by our DTA can significantly improve the model's robustness to different downstream transfer attacks.
Overcome the Difficulties of NSGA-II via Truthful Crowding Distance with Theoretical Guarantees
Jul 25, 2024Abstract:The NSGA-II is proven to encounter difficulties for more than two objectives, and the deduced reason is the crowding distance computed by regarding the different objectives independently. The recent theoretical efficiency of the NSGA-III and the SMS-EMOA also supports the deduced reason as both algorithms consider the dependencies of objectives in the second criterion after the non-dominated sorting but with complicated structure or difficult computation. However, there is still a question of whether a simple modification of the original crowding distance can help. This paper proposes such a variant, called truthful crowding distance. This variant inherits the simple structure of summing the component for each objective. For each objective, it first sorts the set of solutions in order of descending objective values, and uses the smallest normalized L1 distance between the current solution and solutions in the earlier positions of the sorted list as the component. Summing up all components gives the value of truthful crowding distance. We call this NSGA-II variant by NSGA-II-T that replaces the original crowding distance with the truthful one, and that sequentially updates the crowding distance value after each removal. We prove that the NSGA-II-T can efficiently cover the full Pareto front for many-objective mOneMinMax and mOJZJ, in contrast to the exponential runtime of the original NSGA-II. Besides, we also prove that it theoretically achieves a slightly better approximation of the Pareto front for OneMinMax than the original NSGA-II with sequential survival selection. Besides, it is the first NSGA-II variant with a simple structure that performs well for many objectives with theoretical guarantees.
Runtime Analysis of the SMS-EMOA for Many-Objective Optimization
Dec 16, 2023
Abstract:The widely used multiobjective optimizer NSGA-II was recently proven to have considerable difficulties in many-objective optimization. In contrast, experimental results in the literature show a good performance of the SMS-EMOA, which can be seen as a steady-state NSGA-II that uses the hypervolume contribution instead of the crowding distance as the second selection criterion. This paper conducts the first rigorous runtime analysis of the SMS-EMOA for many-objective optimization. To this aim, we first propose a many-objective counterpart, the m-objective mOJZJ problem, of the bi-objective OJZJ benchmark, which is the first many-objective multimodal benchmark used in a mathematical runtime analysis. We prove that SMS-EMOA computes the full Pareto front of this benchmark in an expected number of $O(M^2 n^k)$ iterations, where $n$ denotes the problem size (length of the bit-string representation), $k$ the gap size (a difficulty parameter of the problem), and $M=(2n/m-2k+3)^{m/2}$ the size of the Pareto front. This result together with the existing negative result on the original NSGA-II shows that in principle, the general approach of the NSGA-II is suitable for many-objective optimization, but the crowding distance as tie-breaker has deficiencies. We obtain three additional insights on the SMS-EMOA. Different from a recent result for the bi-objective OJZJ benchmark, the stochastic population update often does not help for mOJZJ. It results in a $1/\Theta(\min\{Mk^{1/2}/2^{k/2},1\})$ speed-up, which is $\Theta(1)$ for large $m$ such as $m>k$. On the positive side, we prove that heavy-tailed mutation still results in a speed-up of order $k^{0.5+k-\beta}$. Finally, we conduct the first runtime analyses of the SMS-EMOA on the bi-objective OneMinMax and LOTZ benchmarks and show that it has a performance comparable to the GSEMO and the NSGA-II.
Theoretical Analyses of Evolutionary Algorithms on Time-Linkage OneMax with General Weights
May 11, 2023Abstract:Evolutionary computation has shown its superiority in dynamic optimization, but for the (dynamic) time-linkage problems, some theoretical studies have revealed the possible weakness of evolutionary computation. Since the theoretically analyzed time-linkage problem only considers the influence of an extremely strong negative time-linkage effect, it remains unclear whether the weakness also appears in problems with more general time-linkage effects. Besides, understanding in depth the relationship between time-linkage effect and algorithmic features is important to build up our knowledge of what algorithmic features are good at what kinds of problems. In this paper, we analyze the general time-linkage effect and consider the time-linkage OneMax with general weights whose absolute values reflect the strength and whose sign reflects the positive or negative influence. We prove that except for some small and positive time-linkage effects (that is, for weights $0$ and $1$), randomized local search (RLS) and (1+1)EA cannot converge to the global optimum with a positive probability. More precisely, for the negative time-linkage effect (for negative weights), both algorithms cannot efficiently reach the global optimum and the probability of failing to converge to the global optimum is at least $1-o(1)$. For the not so small positive time-linkage effect (positive weights greater than $1$), such a probability is at most $c+o(1)$ where $c$ is a constant strictly less than $1$.
Runtime Analysis for the NSGA-II: Proving, Quantifying, and Explaining the Inefficiency For Many Objectives
Dec 08, 2022


Abstract:The NSGA-II is one of the most prominent algorithms to solve multi-objective optimization problems. Despite numerous successful applications, several studies have shown that the NSGA-II is less effective for larger numbers of objectives. In this work, we use mathematical runtime analyses to rigorously demonstrate and quantify this phenomenon. We show that even on the simple OneMinMax benchmark, where every solution is Pareto optimal, the NSGA-II also with large population sizes cannot compute the full Pareto front (objective vectors of all Pareto optima) in sub-exponential time when the number of objectives is at least three. Our proofs suggest that the reason for this unexpected behavior lies in the fact that in the computation of the crowding distance, the different objectives are regarded independently. This is not a problem for two objectives, where any sorting of a pair-wise incomparable set of solutions according to one objective is also such a sorting according to the other objective (in the inverse order).
From Understanding Genetic Drift to a Smart-Restart Mechanism for Estimation-of-Distribution Algorithms
Jun 22, 2022



Abstract:Estimation-of-distribution algorithms (EDAs) are optimization algorithms that learn a distribution on the search space from which good solutions can be sampled easily. A key parameter of most EDAs is the sample size (population size). If the population size is too small, the update of the probabilistic model builds on few samples, leading to the undesired effect of genetic drift. Too large population sizes avoid genetic drift, but slow down the process. Building on a recent quantitative analysis of how the population size leads to genetic drift, we design a smart-restart mechanism for EDAs. By stopping runs when the risk for genetic drift is high, it automatically runs the EDA in good parameter regimes. Via a mathematical runtime analysis, we prove a general performance guarantee for this smart-restart scheme. This in particular shows that in many situations where the optimal (problem-specific) parameter values are known, the restart scheme automatically finds these, leading to the asymptotically optimal performance. We also conduct an extensive experimental analysis. On four classic benchmark problems, we clearly observe the critical influence of the population size on the performance, and we find that the smart-restart scheme leads to a performance close to the one obtainable with optimal parameter values. Our results also show that previous theory-based suggestions for the optimal population size can be far from the optimal ones, leading to a performance clearly inferior to the one obtained via the smart-restart scheme. We also conduct experiments with PBIL (cross-entropy algorithm) on two combinatorial optimization problems from the literature, the max-cut problem and the bipartition problem. Again, we observe that the smart-restart mechanism finds much better values for the population size than those suggested in the literature, leading to a much better performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge