Theoretical Analysis of Quality Diversity Algorithms for a Classical Path Planning Problem

Quality diversity (QD) algorithms have shown to provide sets of high quality solutions for challenging problems in robotics, games, and combinatorial optimisation. So far, theoretical foundational explaining their good behaviour in practice lack far behind their practical success. We contribute to the theoretical understanding of these algorithms and study the behaviour of QD algorithms for a classical planning problem seeking several solutions. We study the all-pairs-shortest-paths (APSP) problem which gives a natural formulation of the behavioural space based on all pairs of nodes of the given input graph that can be used by Map-Elites QD algorithms. Our results show that Map-Elites QD algorithms are able to compute a shortest path for each pair of nodes efficiently in parallel. Furthermore, we examine parent selection techniques for crossover that exhibit significant speed ups compared to the standard QD approach.

Illustrating the Efficiency of Popular Evolutionary Multi-Objective Algorithms Using Runtime Analysis

Runtime analysis has recently been applied to popular evolutionary multi-objective (EMO) algorithms like NSGA-II in order to establish a rigorous theoretical foundation. However, most analyses showed that these algorithms have the same performance guarantee as the simple (G)SEMO algorithm. To our knowledge, there are no runtime analyses showing an advantage of a popular EMO algorithm over the simple algorithm for deterministic problems. We propose such a problem and use it to showcase the superiority of popular EMO algorithms over (G)SEMO: OneTrapZeroTrap is a straightforward generalization of the well-known Trap function to two objectives. We prove that, while GSEMO requires at least $n^n$ expected fitness evaluations to optimise OneTrapZeroTrap, popular EMO algorithms NSGA-II, NSGA-III and SMS-EMOA, all enhanced with a mild diversity mechanism of avoiding genotype duplication, only require $O(n \log n)$ expected fitness evaluations. Our analysis reveals the importance of the key components in each of these sophisticated algorithms and contributes to a better understanding of their capabilities.

Runtime Analyses of NSGA-III on Many-Objective Problems

NSGA-II and NSGA-III are two of the most popular evolutionary multi-objective algorithms used in practice. While NSGA-II is used for few objectives such as 2 and 3, NSGA-III is designed to deal with a larger number of objectives. In a recent breakthrough, Wietheger and Doerr (IJCAI 2023) gave the first runtime analysis for NSGA-III on the 3-objective OneMinMax problem, showing that this state-of-the-art algorithm can be analyzed rigorously. We advance this new line of research by presenting the first runtime analyses of NSGA-III on the popular many-objective benchmark problems mLOTZ, mOMM, and mCOCZ, for an arbitrary constant number $m$ of objectives. Our analysis provides ways to set the important parameters of the algorithm: the number of reference points and the population size, so that a good performance can be guaranteed. We show how these parameters should be scaled with the problem dimension, the number of objectives and the fitness range. To our knowledge, these are the first runtime analyses for NSGA-III for more than 3 objectives.

Analysing the Robustness of NSGA-II under Noise

Runtime analysis has produced many results on the efficiency of simple evolutionary algorithms like the (1+1) EA, and its analogue called GSEMO in evolutionary multiobjective optimisation (EMO). Recently, the first runtime analyses of the famous and highly cited EMO algorithm NSGA-II have emerged, demonstrating that practical algorithms with thousands of applications can be rigorously analysed. However, these results only show that NSGA-II has the same performance guarantees as GSEMO and it is unclear how and when NSGA-II can outperform GSEMO. We study this question in noisy optimisation and consider a noise model that adds large amounts of posterior noise to all objectives with some constant probability $p$ per evaluation. We show that GSEMO fails badly on every noisy fitness function as it tends to remove large parts of the population indiscriminately. In contrast, NSGA-II is able to handle the noise efficiently on \textsc{LeadingOnesTrailingZeroes} when $p<1/2$, as the algorithm is able to preserve useful search points even in the presence of noise. We identify a phase transition at $p=1/2$ where the expected time to cover the Pareto front changes from polynomial to exponential. To our knowledge, this is the first proof that NSGA-II can outperform GSEMO and the first runtime analysis of NSGA-II in noisy optimisation.

A Proof that Using Crossover Can Guarantee Exponential Speed-Ups in Evolutionary Multi-Objective Optimisation

Evolutionary algorithms are popular algorithms for multiobjective optimisation (also called Pareto optimisation) as they use a population to store trade-offs between different objectives. Despite their popularity, the theoretical foundation of multiobjective evolutionary optimisation (EMO) is still in its early development. Fundamental questions such as the benefits of the crossover operator are still not fully understood. We provide a theoretical analysis of well-known EMO algorithms GSEMO and NSGA-II to showcase the possible advantages of crossover. We propose a class of problems on which these EMO algorithms using crossover find the Pareto set in expected polynomial time. In sharp contrast, they and many other EMO algorithms without crossover require exponential time to even find a single Pareto-optimal point. This is the first example of an exponential performance gap through the use of crossover for the widely used NSGA-II algorithm.

Runtime Analysis of Fitness-Proportionate Selection on Linear Functions

This paper extends the runtime analysis of non-elitist evolutionary algorithms (EAs) with fitness-proportionate selection from the simple OneMax function to the linear functions. Not only does our analysis cover a larger class of fitness functions, it also holds for a wider range of mutation rates. We show that with overwhelmingly high probability, no linear function can be optimised in less than exponential time, assuming bitwise mutation rate $\Theta(1/n)$ and population size $\lambda=n^k$ for any constant $k>2$. In contrast to this negative result, we also show that for any linear function with polynomially bounded weights, the EA achieves a polynomial expected runtime if the mutation rate is reduced to $\Theta(1/n^2)$ and the population size is sufficiently large. Furthermore, the EA with mutation rate $\chi/n=\Theta(1/n)$ and modest population size $\lambda=\Omega(\ln n)$ optimises the scaled fitness function $e^{(\chi+\varepsilon)f(x)}$ for any linear function $f$ and any $\varepsilon>0$ in expected time $O(n\lambda\ln\lambda+n^2)$. These upper bounds also extend to some additively decomposed fitness functions, such as the Royal Road functions. We expect that the obtained results may be useful not only for the development of the theory of evolutionary algorithms, but also for biological applications, such as the directed evolution.

Level-Based Analysis of the Univariate Marginal Distribution Algorithm

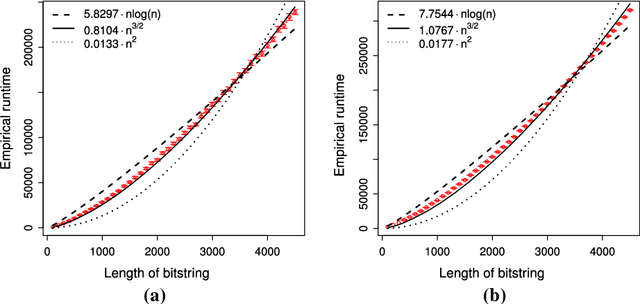
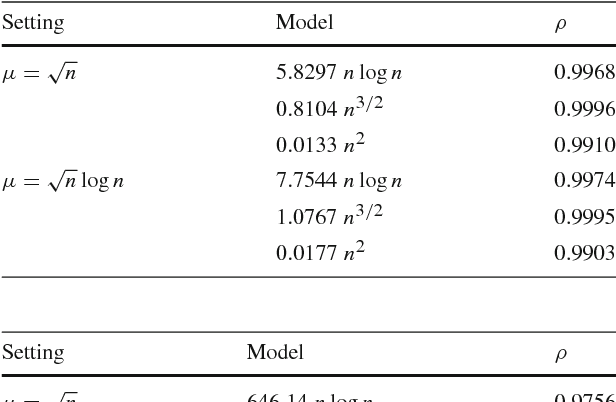
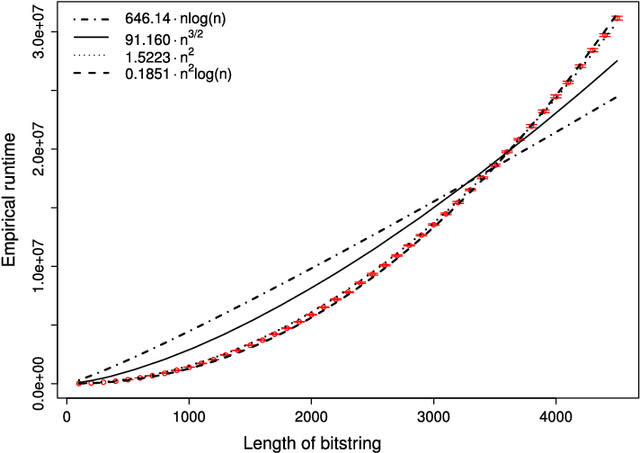
Estimation of Distribution Algorithms (EDAs) are stochastic heuristics that search for optimal solutions by learning and sampling from probabilistic models. Despite their popularity in real-world applications, there is little rigorous understanding of their performance. Even for the Univariate Marginal Distribution Algorithm (UMDA) -- a simple population-based EDA assuming independence between decision variables -- the optimisation time on the linear problem OneMax was until recently undetermined. The incomplete theoretical understanding of EDAs is mainly due to lack of appropriate analytical tools. We show that the recently developed level-based theorem for non-elitist populations combined with anti-concentration results yield upper bounds on the expected optimisation time of the UMDA. This approach results in the bound $\mathcal{O}(n\lambda\log \lambda+n^2)$ on two problems, LeadingOnes and BinVal, for population sizes $\lambda>\mu=\Omega(\log n)$, where $\mu$ and $\lambda$ are parameters of the algorithm. We also prove that the UMDA with population sizes $\mu\in \mathcal{O}(\sqrt{n}) \cap \Omega(\log n)$ optimises OneMax in expected time $\mathcal{O}(\lambda n)$, and for larger population sizes $\mu=\Omega(\sqrt{n}\log n)$, in expected time $\mathcal{O}(\lambda\sqrt{n})$. The facility and generality of our arguments suggest that this is a promising approach to derive bounds on the expected optimisation time of EDAs.

Level-based Analysis of Genetic Algorithms and other Search Processes

Understanding how the time-complexity of evolutionary algorithms (EAs) depend on their parameter settings and characteristics of fitness landscapes is a fundamental problem in evolutionary computation. Most rigorous results were derived using a handful of key analytic techniques, including drift analysis. However, since few of these techniques apply effortlessly to population-based EAs, most time-complexity results concern simplified EAs, such as the (1+1) EA. This paper describes the level-based theorem, a new technique tailored to population-based processes. It applies to any non-elitist process where offspring are sampled independently from a distribution depending only on the current population. Given conditions on this distribution, our technique provides upper bounds on the expected time until the process reaches a target state. We demonstrate the technique on several pseudo-Boolean functions, the sorting problem, and approximation of optimal solutions in combinatorial optimisation. The conditions of the theorem are often straightforward to verify, even for Genetic Algorithms and Estimation of Distribution Algorithms which were considered highly non-trivial to analyse. Finally, we prove that the theorem is nearly optimal for the processes considered. Given the information the theorem requires about the process, a much tighter bound cannot be proved.

Escaping Local Optima using Crossover with Emergent or Reinforced Diversity

Population diversity is essential for avoiding premature convergence in Genetic Algorithms (GAs) and for the effective use of crossover. Yet the dynamics of how diversity emerges in populations are not well understood. We use rigorous runtime analysis to gain insight into population dynamics and GA performance for the ($\mu$+1) GA and the $\text{Jump}_k$ test function. We show that the interplay of crossover and mutation may serve as a catalyst leading to a sudden burst of diversity. This leads to improvements of the expected optimisation time of order $\Omega(n/\log n)$ compared to mutation-only algorithms like (1+1) EA. Moreover, increasing the mutation rate by an arbitrarily small constant factor can facilitate the generation of diversity, leading to speedups of order $\Omega(n)$. We also compare seven commonly used diversity mechanisms and evaluate their impact on runtime bounds for the ($\mu$+1) GA. All previous results in this context only hold for unrealistically low crossover probability $p_c=O(k/n)$, while we give analyses for the setting of constant $p_c < 1$ in all but one case. For the typical case of constant $k > 2$ and constant $p_c$, we can compare the resulting expected runtimes for different diversity mechanisms assuming an optimal choice of $\mu$: $O(n^{k-1})$ for duplicate elimination/minim., $O(n^2\log n)$ for maximising the convex hull, $O(n\log n)$ for deterministic crowding (assuming $p_c = k/n$), $O(n\log n)$ for maximising Hamming distance, $O(n\log n)$ for fitness sharing, $O(n\log n)$ for single-receiver island model. This proves a sizeable advantage of all variants of the ($\mu$+1) GA compared to (1+1) EA, which requires time $\Theta(n^k)$. Experiments complement our theoretical findings and further highlight the benefits of crossover and diversity on $\text{Jump}_k$.

Populations can be essential in tracking dynamic optima

Real-world optimisation problems are often dynamic. Previously good solutions must be updated or replaced due to changes in objectives and constraints. It is often claimed that evolutionary algorithms are particularly suitable for dynamic optimisation because a large population can contain different solutions that may be useful in the future. However, rigorous theoretical demonstrations for how populations in dynamic optimisation can be essential are sparse and restricted to special cases. This paper provides theoretical explanations of how populations can be essential in evolutionary dynamic optimisation in a general and natural setting. We describe a natural class of dynamic optimisation problems where a sufficiently large population is necessary to keep track of moving optima reliably. We establish a relationship between the population-size and the probability that the algorithm loses track of the optimum.