Level-Based Analysis of the Univariate Marginal Distribution Algorithm

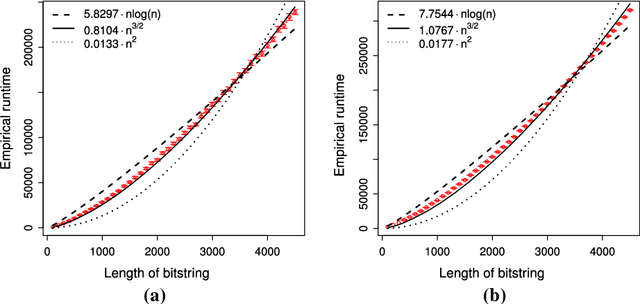
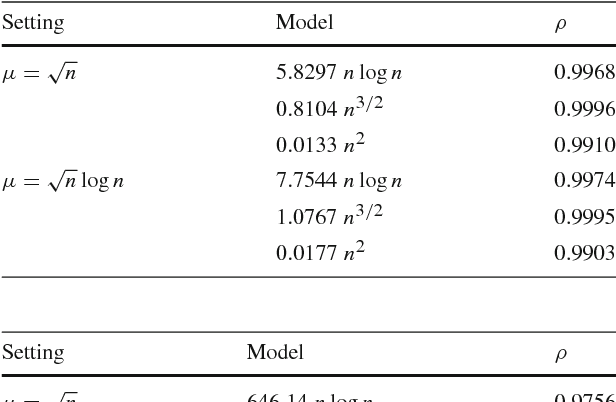
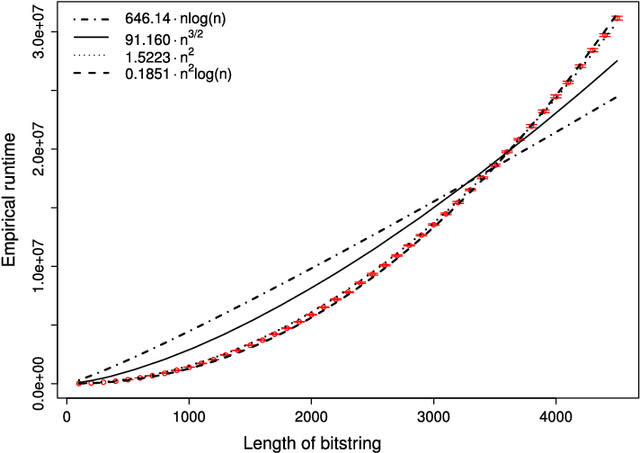
Estimation of Distribution Algorithms (EDAs) are stochastic heuristics that search for optimal solutions by learning and sampling from probabilistic models. Despite their popularity in real-world applications, there is little rigorous understanding of their performance. Even for the Univariate Marginal Distribution Algorithm (UMDA) -- a simple population-based EDA assuming independence between decision variables -- the optimisation time on the linear problem OneMax was until recently undetermined. The incomplete theoretical understanding of EDAs is mainly due to lack of appropriate analytical tools. We show that the recently developed level-based theorem for non-elitist populations combined with anti-concentration results yield upper bounds on the expected optimisation time of the UMDA. This approach results in the bound $\mathcal{O}(n\lambda\log \lambda+n^2)$ on two problems, LeadingOnes and BinVal, for population sizes $\lambda>\mu=\Omega(\log n)$, where $\mu$ and $\lambda$ are parameters of the algorithm. We also prove that the UMDA with population sizes $\mu\in \mathcal{O}(\sqrt{n}) \cap \Omega(\log n)$ optimises OneMax in expected time $\mathcal{O}(\lambda n)$, and for larger population sizes $\mu=\Omega(\sqrt{n}\log n)$, in expected time $\mathcal{O}(\lambda\sqrt{n})$. The facility and generality of our arguments suggest that this is a promising approach to derive bounds on the expected optimisation time of EDAs.