On the Limitations of the Univariate Marginal Distribution Algorithm to Deception and Where Bivariate EDAs might help

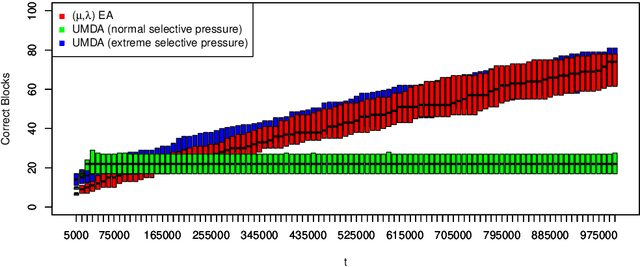
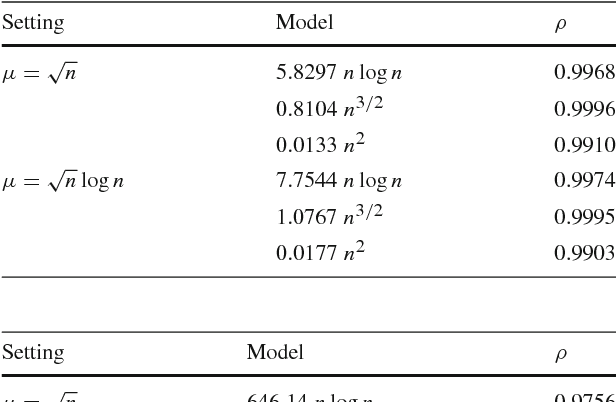
We introduce a new benchmark problem called Deceptive Leading Blocks (DLB) to rigorously study the runtime of the Univariate Marginal Distribution Algorithm (UMDA) in the presence of epistasis and deception. We show that simple Evolutionary Algorithms (EAs) outperform the UMDA unless the selective pressure $\mu/\lambda$ is extremely high, where $\mu$ and $\lambda$ are the parent and offspring population sizes, respectively. More precisely, we show that the UMDA with a parent population size of $\mu=\Omega(\log n)$ has an expected runtime of $e^{\Omega(\mu)}$ on the DLB problem assuming any selective pressure $\frac{\mu}{\lambda} \geq \frac{14}{1000}$, as opposed to the expected runtime of $\mathcal{O}(n\lambda\log \lambda+n^3)$ for the non-elitist $(\mu,\lambda)~\text{EA}$ with $\mu/\lambda\leq 1/e$. These results illustrate inherent limitations of univariate EDAs against deception and epistasis, which are common characteristics of real-world problems. In contrast, empirical evidence reveals the efficiency of the bi-variate MIMIC algorithm on the DLB problem. Our results suggest that one should consider EDAs with more complex probabilistic models when optimising problems with some degree of epistasis and deception.

Runtime Analysis of the Univariate Marginal Distribution Algorithm under Low Selective Pressure and Prior Noise

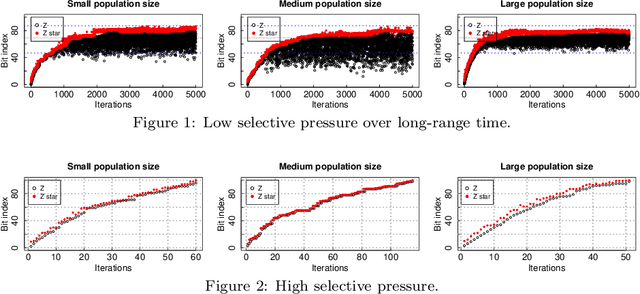
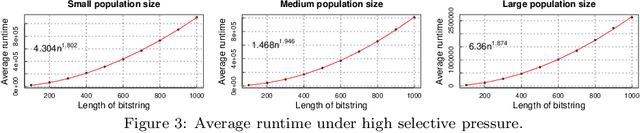
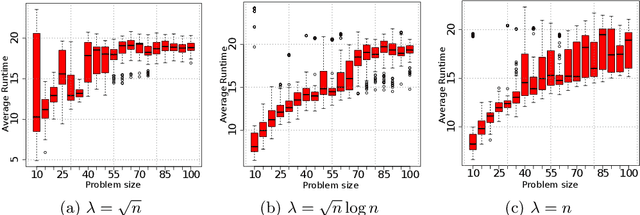
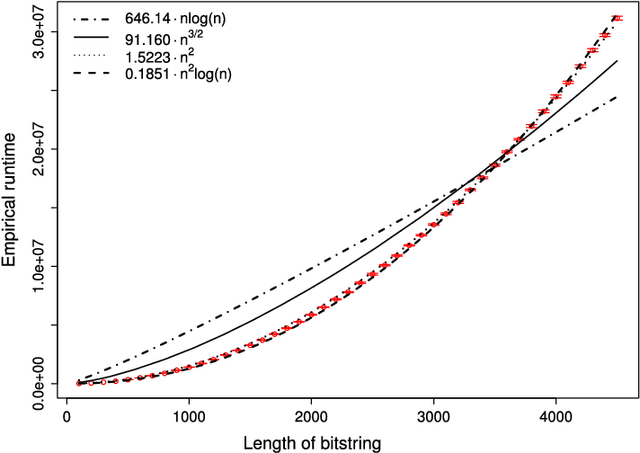
We perform a rigorous runtime analysis for the Univariate Marginal Distribution Algorithm on the LeadingOnes function, a well-known benchmark function in the theory community of evolutionary computation with a high correlation between decision variables. For a problem instance of size $n$, the currently best known upper bound on the expected runtime is $\mathcal{O}(n\lambda\log\lambda+n^2)$ (Dang and Lehre, GECCO 2015), while a lower bound necessary to understand how the algorithm copes with variable dependencies is still missing. Motivated by this, we show that the algorithm requires a $e^{\Omega(\mu)}$ runtime with high probability and in expectation if the selective pressure is low; otherwise, we obtain a lower bound of $\Omega(\frac{n\lambda}{\log(\lambda-\mu)})$ on the expected runtime. Furthermore, we for the first time consider the algorithm on the function under a prior noise model and obtain an $\mathcal{O}(n^2)$ expected runtime for the optimal parameter settings. In the end, our theoretical results are accompanied by empirical findings, not only matching with rigorous analyses but also providing new insights into the behaviour of the algorithm.

Level-Based Analysis of the Univariate Marginal Distribution Algorithm

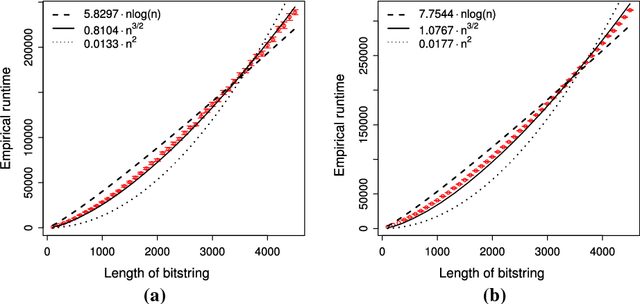
Estimation of Distribution Algorithms (EDAs) are stochastic heuristics that search for optimal solutions by learning and sampling from probabilistic models. Despite their popularity in real-world applications, there is little rigorous understanding of their performance. Even for the Univariate Marginal Distribution Algorithm (UMDA) -- a simple population-based EDA assuming independence between decision variables -- the optimisation time on the linear problem OneMax was until recently undetermined. The incomplete theoretical understanding of EDAs is mainly due to lack of appropriate analytical tools. We show that the recently developed level-based theorem for non-elitist populations combined with anti-concentration results yield upper bounds on the expected optimisation time of the UMDA. This approach results in the bound $\mathcal{O}(n\lambda\log \lambda+n^2)$ on two problems, LeadingOnes and BinVal, for population sizes $\lambda>\mu=\Omega(\log n)$, where $\mu$ and $\lambda$ are parameters of the algorithm. We also prove that the UMDA with population sizes $\mu\in \mathcal{O}(\sqrt{n}) \cap \Omega(\log n)$ optimises OneMax in expected time $\mathcal{O}(\lambda n)$, and for larger population sizes $\mu=\Omega(\sqrt{n}\log n)$, in expected time $\mathcal{O}(\lambda\sqrt{n})$. The facility and generality of our arguments suggest that this is a promising approach to derive bounds on the expected optimisation time of EDAs.

Level-Based Analysis of the Population-Based Incremental Learning Algorithm

The Population-Based Incremental Learning (PBIL) algorithm uses a convex combination of the current model and the empirical model to construct the next model, which is then sampled to generate offspring. The Univariate Marginal Distribution Algorithm (UMDA) is a special case of the PBIL, where the current model is ignored. Dang and Lehre (GECCO 2015) showed that UMDA can optimise LeadingOnes efficiently. The question still remained open if the PBIL performs equally well. Here, by applying the level-based theorem in addition to Dvoretzky--Kiefer--Wolfowitz inequality, we show that the PBIL optimises function LeadingOnes in expected time $\mathcal{O}(n\lambda \log \lambda + n^2)$ for a population size $\lambda = \Omega(\log n)$, which matches the bound of the UMDA. Finally, we show that the result carries over to BinVal, giving the fist runtime result for the PBIL on the BinVal problem.

Memetic Algorithms Beat Evolutionary Algorithms on the Class of Hurdle Problems

Memetic algorithms are popular hybrid search heuristics that integrate local search into the search process of an evolutionary algorithm in order to combine the advantages of rapid exploitation and global optimisation. However, these algorithms are not well understood and the field is lacking a solid theoretical foundation that explains when and why memetic algorithms are effective. We provide a rigorous runtime analysis of a simple memetic algorithm, the $(1+1)$ MA, on the Hurdle problem class, a landscape class of tuneable difficulty that shows a "big valley structure", a characteristic feature of many hard problems from combinatorial optimisation. The only parameter of this class is the hurdle width w, which describes the length of fitness valleys that have to be overcome. We show that the $(1+1)$ EA requires $\Theta(n^w)$ expected function evaluations to find the optimum, whereas the $(1+1)$ MA with best-improvement and first-improvement local search can find the optimum in $\Theta(n^2+n^3/w^2)$ and $\Theta(n^3/w^2)$ function evaluations, respectively. Surprisingly, while increasing the hurdle width makes the problem harder for evolutionary algorithms, the problem becomes easier for memetic algorithms. We discuss how these findings can explain and illustrate the success of memetic algorithms for problems with big valley structures.

Improved Runtime Bounds for the Univariate Marginal Distribution Algorithm via Anti-Concentration

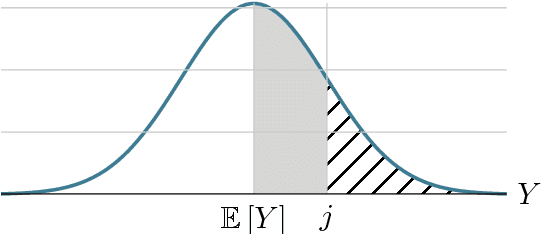
Unlike traditional evolutionary algorithms which produce offspring via genetic operators, Estimation of Distribution Algorithms (EDAs) sample solutions from probabilistic models which are learned from selected individuals. It is hoped that EDAs may improve optimisation performance on epistatic fitness landscapes by learning variable interactions. However, hardly any rigorous results are available to support claims about the performance of EDAs, even for fitness functions without epistasis. The expected runtime of the Univariate Marginal Distribution Algorithm (UMDA) on OneMax was recently shown to be in $\mathcal{O}\left(n\lambda\log \lambda\right)$ by Dang and Lehre (GECCO 2015). Later, Krejca and Witt (FOGA 2017) proved the lower bound $\Omega\left(\lambda\sqrt{n}+n\log n\right)$ via an involved drift analysis. We prove a $\mathcal{O}\left(n\lambda\right)$ bound, given some restrictions on the population size. This implies the tight bound $\Theta\left(n\log n\right)$ when $\lambda=\mathcal{O}\left(\log n\right)$, matching the runtime of classical EAs. Our analysis uses the level-based theorem and anti-concentration properties of the Poisson-Binomial distribution. We expect that these generic methods will facilitate further analysis of EDAs.