Improved Runtime Bounds for the Univariate Marginal Distribution Algorithm via Anti-Concentration
Paper and Code
Feb 02, 2018
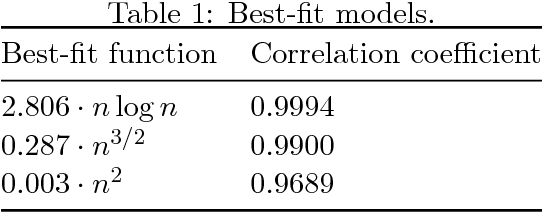
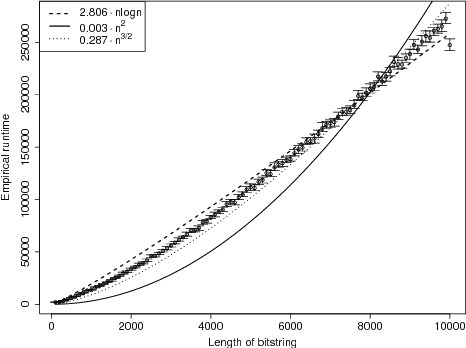
Unlike traditional evolutionary algorithms which produce offspring via genetic operators, Estimation of Distribution Algorithms (EDAs) sample solutions from probabilistic models which are learned from selected individuals. It is hoped that EDAs may improve optimisation performance on epistatic fitness landscapes by learning variable interactions. However, hardly any rigorous results are available to support claims about the performance of EDAs, even for fitness functions without epistasis. The expected runtime of the Univariate Marginal Distribution Algorithm (UMDA) on OneMax was recently shown to be in $\mathcal{O}\left(n\lambda\log \lambda\right)$ by Dang and Lehre (GECCO 2015). Later, Krejca and Witt (FOGA 2017) proved the lower bound $\Omega\left(\lambda\sqrt{n}+n\log n\right)$ via an involved drift analysis. We prove a $\mathcal{O}\left(n\lambda\right)$ bound, given some restrictions on the population size. This implies the tight bound $\Theta\left(n\log n\right)$ when $\lambda=\mathcal{O}\left(\log n\right)$, matching the runtime of classical EAs. Our analysis uses the level-based theorem and anti-concentration properties of the Poisson-Binomial distribution. We expect that these generic methods will facilitate further analysis of EDAs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge