Runtime analysis of a coevolutionary algorithm on impartial combinatorial games

Due to their complex dynamics, combinatorial games are a key test case and application for algorithms that train game playing agents. Among those algorithms that train using self-play are coevolutionary algorithms (CoEAs). CoEAs evolve a population of individuals by iteratively selecting the strongest based on their interactions against contemporaries, and using those selected as parents for the following generation (via randomised mutation and crossover). However, the successful application of CoEAs for game playing is difficult due to pathological behaviours such as cycling, an issue especially critical for games with intransitive payoff landscapes. Insight into how to design CoEAs to avoid such behaviours can be provided by runtime analysis. In this paper, we push the scope of runtime analysis to combinatorial games, proving a general upper bound for the number of simulated games needed for UMDA (a type of CoEA) to discover (with high probability) an optimal strategy for an impartial combinatorial game. This result applies to any impartial combinatorial game, and for many games the implied bound is polynomial or quasipolynomial as a function of the number of game positions. After proving the main result, we provide several applications to simple well-known games: Nim, Chomp, Silver Dollar, and Turning Turtles. As the first runtime analysis for CoEAs on combinatorial games, this result is a critical step towards a comprehensive theoretical framework for coevolution.

Overcoming Binary Adversarial Optimisation with Competitive Coevolution

Co-evolutionary algorithms (CoEAs), which pair candidate designs with test cases, are frequently used in adversarial optimisation, particularly for binary test-based problems where designs and tests yield binary outcomes. The effectiveness of designs is determined by their performance against tests, and the value of tests is based on their ability to identify failing designs, often leading to more sophisticated tests and improved designs. However, CoEAs can exhibit complex, sometimes pathological behaviours like disengagement. Through runtime analysis, we aim to rigorously analyse whether CoEAs can efficiently solve test-based adversarial optimisation problems in an expected polynomial runtime. This paper carries out the first rigorous runtime analysis of $(1,\lambda)$ CoEA for binary test-based adversarial optimisation problems. In particular, we introduce a binary test-based benchmark problem called \Diagonal problem and initiate the first runtime analysis of competitive CoEA on this problem. The mathematical analysis shows that the $(1,\lambda)$-CoEA can efficiently find an $\varepsilon$ approximation to the optimal solution of the \Diagonal problem, i.e. in expected polynomial runtime assuming sufficiently low mutation rates and large offspring population size. On the other hand, the standard $(1,\lambda)$-EA fails to find an $\varepsilon$ approximation to the optimal solution of the \Diagonal problem in polynomial runtime. This suggests the promising potential of coevolution for solving binary adversarial optimisation problems.

Concentration Tail-Bound Analysis of Coevolutionary and Bandit Learning Algorithms

Runtime analysis, as a branch of the theory of AI, studies how the number of iterations algorithms take before finding a solution (its runtime) depends on the design of the algorithm and the problem structure. Drift analysis is a state-of-the-art tool for estimating the runtime of randomised algorithms, such as evolutionary and bandit algorithms. Drift refers roughly to the expected progress towards the optimum per iteration. This paper considers the problem of deriving concentration tail-bounds on the runtime/regret of algorithms. It provides a novel drift theorem that gives precise exponential tail-bounds given positive, weak, zero and even negative drift. Previously, such exponential tail bounds were missing in the case of weak, zero, or negative drift. Our drift theorem can be used to prove a strong concentration of the runtime/regret of algorithms in AI. For example, we prove that the regret of the \rwab bandit algorithm is highly concentrated, while previous analyses only considered the expected regret. This means that the algorithm obtains the optimum within a given time frame with high probability, i.e. a form of algorithm reliability. Moreover, our theorem implies that the time needed by the co-evolutionary algorithm RLS-PD to obtain a Nash equilibrium in a \bilinear max-min-benchmark problem is highly concentrated. However, we also prove that the algorithm forgets the Nash equilibrium, and the time until this occurs is highly concentrated. This highlights a weakness in the RLS-PD which should be addressed by future work.

Non-Elitist Evolutionary Multi-Objective Optimisation: Proof-of-Principle Results

Elitism, which constructs the new population by preserving best solutions out of the old population and newly-generated solutions, has been a default way for population update since its introduction into multi-objective evolutionary algorithms (MOEAs) in the late 1990s. In this paper, we take an opposite perspective to conduct the population update in MOEAs by simply discarding elitism. That is, we treat the newly-generated solutions as the new population directly (so that all selection pressure comes from mating selection). We propose a simple non-elitist MOEA (called NE-MOEA) that only uses Pareto dominance sorting to compare solutions, without involving any diversity-related selection criterion. Preliminary experimental results show that NE-MOEA can compete with well-known elitist MOEAs (NSGA-II, SMS-EMOA and NSGA-III) on several combinatorial problems. Lastly, we discuss limitations of the proposed non-elitist algorithm and suggest possible future research directions.

Runtime Analysis of Competitive co-Evolutionary Algorithms for Maximin Optimisation of a Bilinear Function

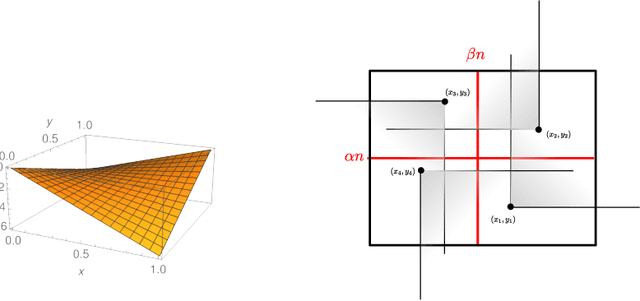
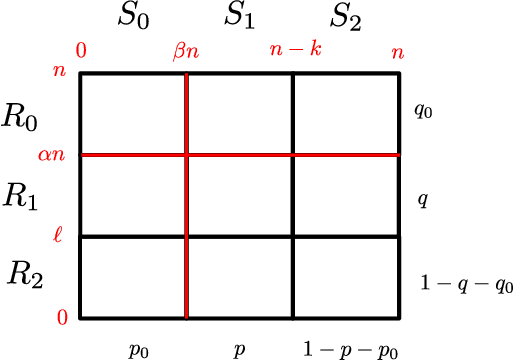
Co-evolutionary algorithms have a wide range of applications, such as in hardware design, evolution of strategies for board games, and patching software bugs. However, these algorithms are poorly understood and applications are often limited by pathological behaviour, such as loss of gradient, relative over-generalisation, and mediocre objective stasis. It is an open challenge to develop a theory that can predict when co-evolutionary algorithms find solutions efficiently and reliable. This paper provides a first step in developing runtime analysis for population-based competitive co-evolutionary algorithms. We provide a mathematical framework for describing and reasoning about the performance of co-evolutionary processes. An example application of the framework shows a scenario where a simple co-evolutionary algorithm obtains a solution in polynomial expected time. Finally, we describe settings where the co-evolutionary algorithm needs exponential time with overwhelmingly high probability to obtain a solution.

Self-adaptation in non-Elitist Evolutionary Algorithms on Discrete Problems with Unknown Structure

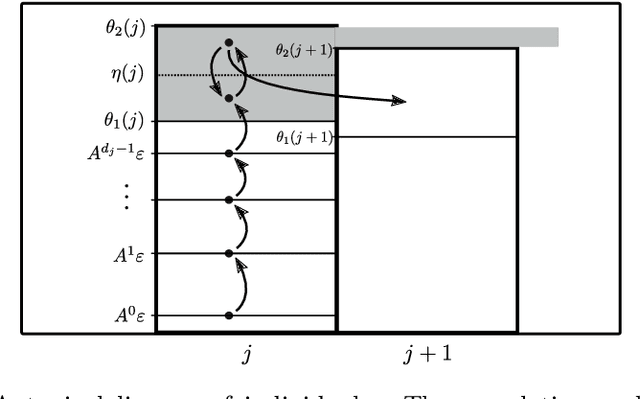
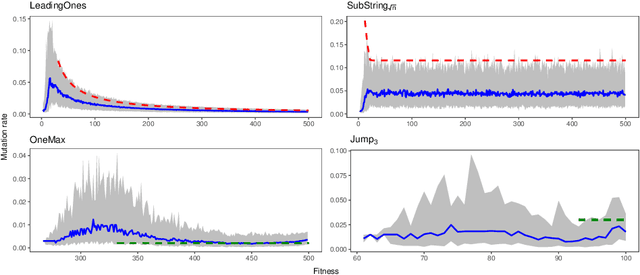
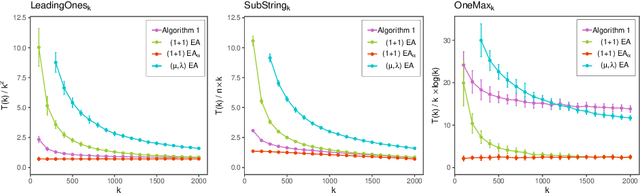
A key challenge to make effective use of evolutionary algorithms is to choose appropriate settings for their parameters. However, the appropriate parameter setting generally depends on the structure of the optimisation problem, which is often unknown to the user. Non-deterministic parameter control mechanisms adjust parameters using information obtained from the evolutionary process. Self-adaptation -- where parameter settings are encoded in the chromosomes of individuals and evolve through mutation and crossover -- is a popular parameter control mechanism in evolutionary strategies. However, there is little theoretical evidence that self-adaptation is effective, and self-adaptation has largely been ignored by the discrete evolutionary computation community. Here we show through a theoretical runtime analysis that a non-elitist, discrete evolutionary algorithm which self-adapts its mutation rate not only outperforms EAs which use static mutation rates on \leadingones, but also improves asymptotically on an EA using a state-of-the-art control mechanism. The structure of this problem depends on a parameter $k$, which is \emph{a priori} unknown to the algorithm, and which is needed to appropriately set a fixed mutation rate. The self-adaptive EA achieves the same asymptotic runtime as if this parameter was known to the algorithm beforehand, which is an asymptotic speedup for this problem compared to all other EAs previously studied. An experimental study of how the mutation-rates evolve show that they respond adequately to a diverse range of problem structures. These results suggest that self-adaptation should be adopted more broadly as a parameter control mechanism in discrete, non-elitist evolutionary algorithms.

Runtime Analysis of Fitness-Proportionate Selection on Linear Functions

This paper extends the runtime analysis of non-elitist evolutionary algorithms (EAs) with fitness-proportionate selection from the simple OneMax function to the linear functions. Not only does our analysis cover a larger class of fitness functions, it also holds for a wider range of mutation rates. We show that with overwhelmingly high probability, no linear function can be optimised in less than exponential time, assuming bitwise mutation rate $\Theta(1/n)$ and population size $\lambda=n^k$ for any constant $k>2$. In contrast to this negative result, we also show that for any linear function with polynomially bounded weights, the EA achieves a polynomial expected runtime if the mutation rate is reduced to $\Theta(1/n^2)$ and the population size is sufficiently large. Furthermore, the EA with mutation rate $\chi/n=\Theta(1/n)$ and modest population size $\lambda=\Omega(\ln n)$ optimises the scaled fitness function $e^{(\chi+\varepsilon)f(x)}$ for any linear function $f$ and any $\varepsilon>0$ in expected time $O(n\lambda\ln\lambda+n^2)$. These upper bounds also extend to some additively decomposed fitness functions, such as the Royal Road functions. We expect that the obtained results may be useful not only for the development of the theory of evolutionary algorithms, but also for biological applications, such as the directed evolution.

On the Limitations of the Univariate Marginal Distribution Algorithm to Deception and Where Bivariate EDAs might help

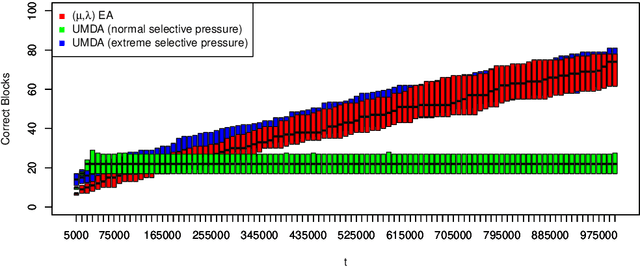
We introduce a new benchmark problem called Deceptive Leading Blocks (DLB) to rigorously study the runtime of the Univariate Marginal Distribution Algorithm (UMDA) in the presence of epistasis and deception. We show that simple Evolutionary Algorithms (EAs) outperform the UMDA unless the selective pressure $\mu/\lambda$ is extremely high, where $\mu$ and $\lambda$ are the parent and offspring population sizes, respectively. More precisely, we show that the UMDA with a parent population size of $\mu=\Omega(\log n)$ has an expected runtime of $e^{\Omega(\mu)}$ on the DLB problem assuming any selective pressure $\frac{\mu}{\lambda} \geq \frac{14}{1000}$, as opposed to the expected runtime of $\mathcal{O}(n\lambda\log \lambda+n^3)$ for the non-elitist $(\mu,\lambda)~\text{EA}$ with $\mu/\lambda\leq 1/e$. These results illustrate inherent limitations of univariate EDAs against deception and epistasis, which are common characteristics of real-world problems. In contrast, empirical evidence reveals the efficiency of the bi-variate MIMIC algorithm on the DLB problem. Our results suggest that one should consider EDAs with more complex probabilistic models when optimising problems with some degree of epistasis and deception.

Runtime Analysis of the Univariate Marginal Distribution Algorithm under Low Selective Pressure and Prior Noise

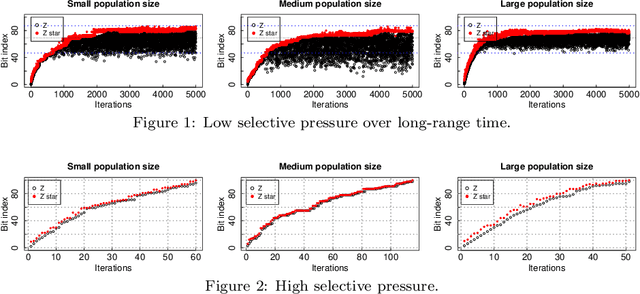
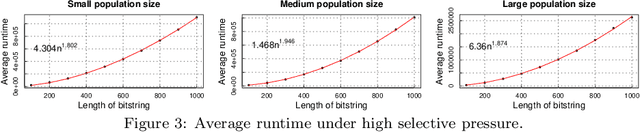
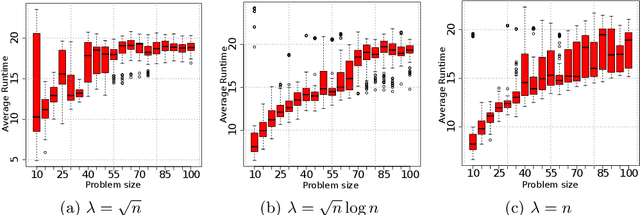
We perform a rigorous runtime analysis for the Univariate Marginal Distribution Algorithm on the LeadingOnes function, a well-known benchmark function in the theory community of evolutionary computation with a high correlation between decision variables. For a problem instance of size $n$, the currently best known upper bound on the expected runtime is $\mathcal{O}(n\lambda\log\lambda+n^2)$ (Dang and Lehre, GECCO 2015), while a lower bound necessary to understand how the algorithm copes with variable dependencies is still missing. Motivated by this, we show that the algorithm requires a $e^{\Omega(\mu)}$ runtime with high probability and in expectation if the selective pressure is low; otherwise, we obtain a lower bound of $\Omega(\frac{n\lambda}{\log(\lambda-\mu)})$ on the expected runtime. Furthermore, we for the first time consider the algorithm on the function under a prior noise model and obtain an $\mathcal{O}(n^2)$ expected runtime for the optimal parameter settings. In the end, our theoretical results are accompanied by empirical findings, not only matching with rigorous analyses but also providing new insights into the behaviour of the algorithm.

Parallel Black-Box Complexity with Tail Bounds

We propose a new black-box complexity model for search algorithms evaluating $\lambda$ search points in parallel. The parallel unary unbiased black-box complexity gives lower bounds on the number of function evaluations every parallel unary unbiased black-box algorithm needs to optimise a given problem. It captures the inertia caused by offspring populations in evolutionary algorithms and the total computational effort in parallel metaheuristics. We present complexity results for LeadingOnes and OneMax. Our main result is a general performance limit: we prove that on every function every $\lambda$-parallel unary unbiased algorithm needs at least $\Omega(\frac{\lambda n}{\ln \lambda} + n \log n)$ evaluations to find any desired target set of up to exponential size, with an overwhelming probability. This yields lower bounds for the typical optimisation time on unimodal and multimodal problems, for the time to find any local optimum, and for the time to even get close to any optimum. The power and versatility of this approach is shown for a wide range of illustrative problems from combinatorial optimisation. Our performance limits can guide parameter choice and algorithm design; we demonstrate the latter by presenting an optimal $\lambda$-parallel algorithm for OneMax that uses parallelism most effectively.