Brendan Case
Self-adaptation in non-Elitist Evolutionary Algorithms on Discrete Problems with Unknown Structure
Apr 01, 2020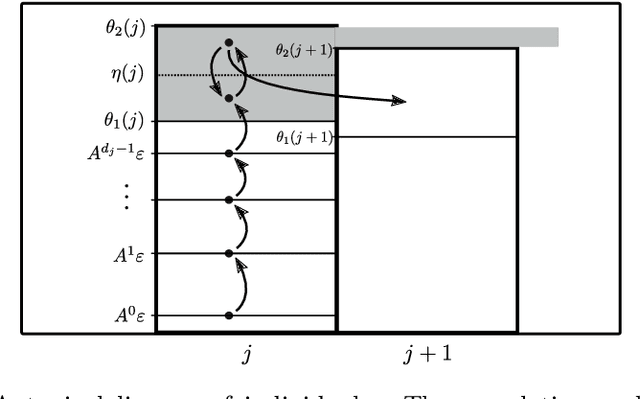
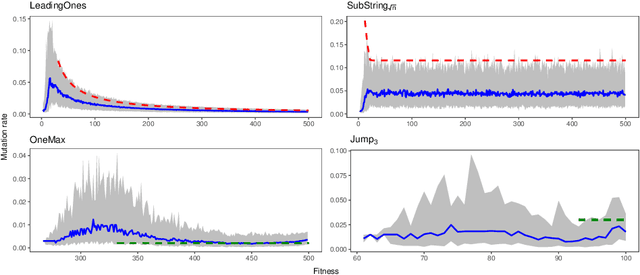
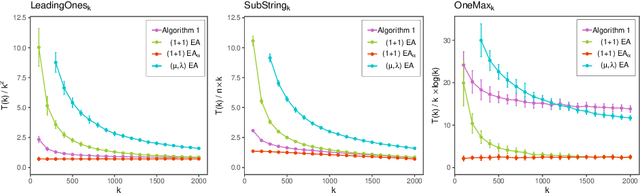
Abstract:A key challenge to make effective use of evolutionary algorithms is to choose appropriate settings for their parameters. However, the appropriate parameter setting generally depends on the structure of the optimisation problem, which is often unknown to the user. Non-deterministic parameter control mechanisms adjust parameters using information obtained from the evolutionary process. Self-adaptation -- where parameter settings are encoded in the chromosomes of individuals and evolve through mutation and crossover -- is a popular parameter control mechanism in evolutionary strategies. However, there is little theoretical evidence that self-adaptation is effective, and self-adaptation has largely been ignored by the discrete evolutionary computation community. Here we show through a theoretical runtime analysis that a non-elitist, discrete evolutionary algorithm which self-adapts its mutation rate not only outperforms EAs which use static mutation rates on \leadingones, but also improves asymptotically on an EA using a state-of-the-art control mechanism. The structure of this problem depends on a parameter $k$, which is \emph{a priori} unknown to the algorithm, and which is needed to appropriately set a fixed mutation rate. The self-adaptive EA achieves the same asymptotic runtime as if this parameter was known to the algorithm beforehand, which is an asymptotic speedup for this problem compared to all other EAs previously studied. An experimental study of how the mutation-rates evolve show that they respond adequately to a diverse range of problem structures. These results suggest that self-adaptation should be adopted more broadly as a parameter control mechanism in discrete, non-elitist evolutionary algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge