On the Limitations of the Univariate Marginal Distribution Algorithm to Deception and Where Bivariate EDAs might help
Paper and Code
Jul 29, 2019
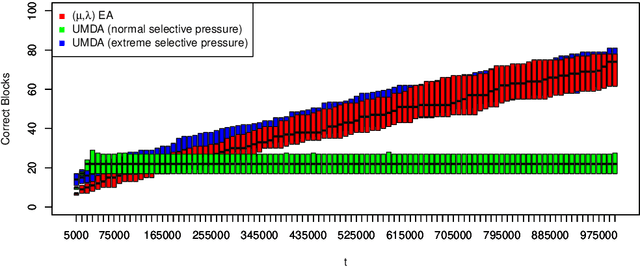
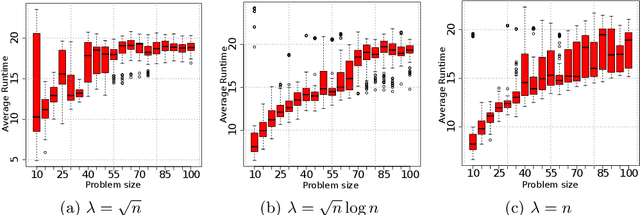
We introduce a new benchmark problem called Deceptive Leading Blocks (DLB) to rigorously study the runtime of the Univariate Marginal Distribution Algorithm (UMDA) in the presence of epistasis and deception. We show that simple Evolutionary Algorithms (EAs) outperform the UMDA unless the selective pressure $\mu/\lambda$ is extremely high, where $\mu$ and $\lambda$ are the parent and offspring population sizes, respectively. More precisely, we show that the UMDA with a parent population size of $\mu=\Omega(\log n)$ has an expected runtime of $e^{\Omega(\mu)}$ on the DLB problem assuming any selective pressure $\frac{\mu}{\lambda} \geq \frac{14}{1000}$, as opposed to the expected runtime of $\mathcal{O}(n\lambda\log \lambda+n^3)$ for the non-elitist $(\mu,\lambda)~\text{EA}$ with $\mu/\lambda\leq 1/e$. These results illustrate inherent limitations of univariate EDAs against deception and epistasis, which are common characteristics of real-world problems. In contrast, empirical evidence reveals the efficiency of the bi-variate MIMIC algorithm on the DLB problem. Our results suggest that one should consider EDAs with more complex probabilistic models when optimising problems with some degree of epistasis and deception.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge