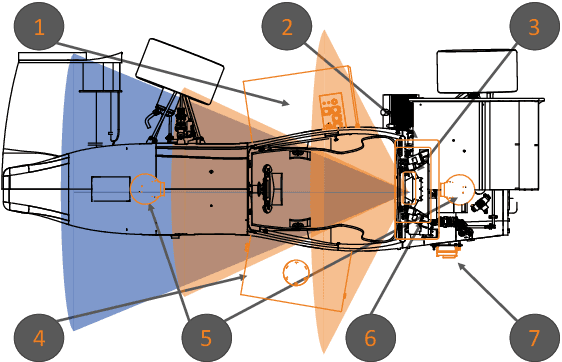
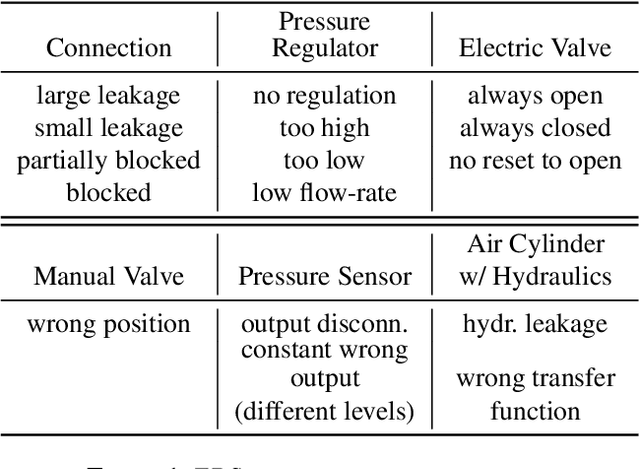
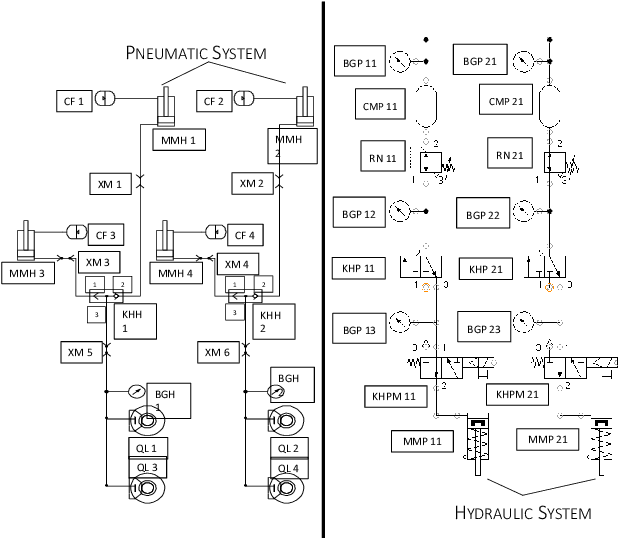
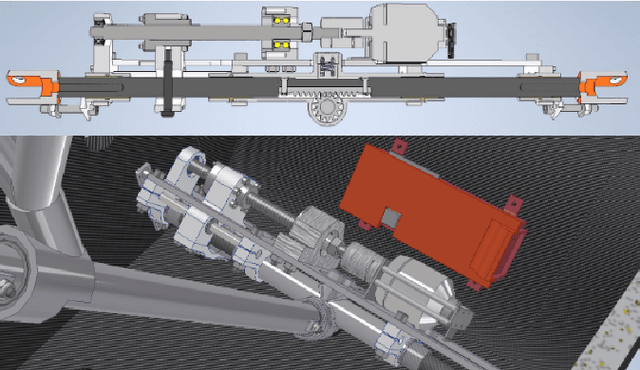
Winning Through Simplicity: Autonomous Car Design for Formula Student

This paper presents the design of an autonomous race car that is self-designed, self-developed, and self-built by the Elefant Racing team at the University of Bayreuth. The system is created to compete in the Formula Student Driverless competition. Its primary focus is on the Acceleration track, a straight 75-meter-long course, and the Skidpad track, which comprises two circles forming an eight. Additionally, it is experimentally capable of competing in the Autocross and Trackdrive events, which feature tracks with previously unknown straights and curves. The paper details the hardware, software and sensor setup employed during the 2020/2021 season. Despite being developed by a small team with limited computer science expertise, the design won the Formula Student East Engineering Design award. Emphasizing simplicity and efficiency, the team employed streamlined techniques to achieve their success.

Analysis of the EA on LeadingOnes with Constraints

Understanding how evolutionary algorithms perform on constrained problems has gained increasing attention in recent years. In this paper, we study how evolutionary algorithms optimize constrained versions of the classical LeadingOnes problem. We first provide a run time analysis for the classical (1+1) EA on the LeadingOnes problem with a deterministic cardinality constraint, giving $\Theta(n (n-B)\log(B) + n^2)$ as the tight bound. Our results show that the behaviour of the algorithm is highly dependent on the constraint bound of the uniform constraint. Afterwards, we consider the problem in the context of stochastic constraints and provide insights using experimental studies on how the ($\mu$+1) EA is able to deal with these constraints in a sampling-based setting.

Temporal Network Creation Games

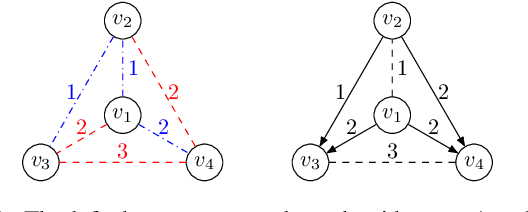
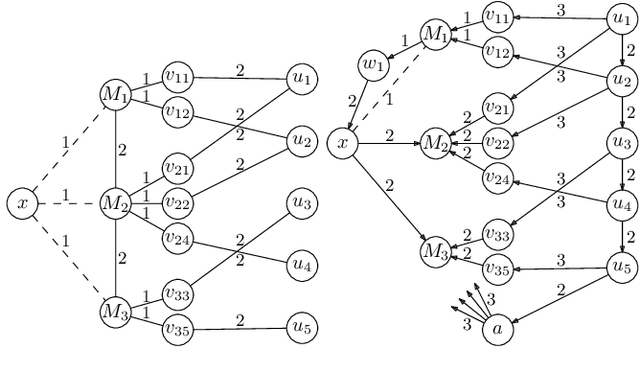
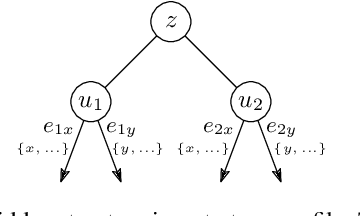
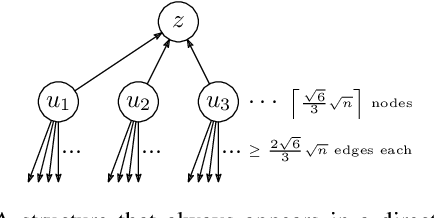
Most networks are not static objects, but instead they change over time. This observation has sparked rigorous research on temporal graphs within the last years. In temporal graphs, we have a fixed set of nodes and the connections between them are only available at certain time steps. This gives rise to a plethora of algorithmic problems on such graphs, most prominently the problem of finding temporal spanners, i.e., the computation of subgraphs that guarantee all pairs reachability via temporal paths. To the best of our knowledge, only centralized approaches for the solution of this problem are known. However, many real-world networks are not shaped by a central designer but instead they emerge and evolve by the interaction of many strategic agents. This observation is the driving force of the recent intensive research on game-theoretic network formation models. In this work we bring together these two recent research directions: temporal graphs and game-theoretic network formation. As a first step into this new realm, we focus on a simplified setting where a complete temporal host graph is given and the agents, corresponding to its nodes, selfishly create incident edges to ensure that they can reach all other nodes via temporal paths in the created network. This yields temporal spanners as equilibria of our game. We prove results on the convergence to and the existence of equilibrium networks, on the complexity of finding best agent strategies, and on the quality of the equilibria. By taking these first important steps, we uncover challenging open problems that call for an in-depth exploration of the creation of temporal graphs by strategic agents.

Evolutionary Diversity Optimisation in Constructing Satisfying Assignments

Computing diverse solutions for a given problem, in particular evolutionary diversity optimisation (EDO), is a hot research topic in the evolutionary computation community. This paper studies the Boolean satisfiability problem (SAT) in the context of EDO. SAT is of great importance in computer science and differs from the other problems studied in EDO literature, such as KP and TSP. SAT is heavily constrained, and the conventional evolutionary operators are inefficient in generating SAT solutions. Our approach avails of the following characteristics of SAT: 1) the possibility of adding more constraints (clauses) to the problem to forbid solutions or to fix variables, and 2) powerful solvers in the literature, such as minisat. We utilise such a solver to construct a diverse set of solutions. Moreover, maximising diversity provides us with invaluable information about the solution space of a given SAT problem, such as how large the feasible region is. In this study, we introduce evolutionary algorithms (EAs) employing a well-known SAT solver to maximise diversity among a set of SAT solutions explicitly. The experimental investigations indicate the introduced algorithms' capability to maximise diversity among the SAT solutions.

Single-Peaked Jump Schelling Games

Schelling games model the wide-spread phenomenon of residential segregation in metropolitan areas from a game-theoretic point of view. In these games agents of different types each strategically select a node on a given graph that models the residential area to maximize their individual utility. The latter solely depends on the types of the agents on neighboring nodes and it has been a standard assumption to consider utility functions that are monotone in the number of same-type neighbors. This simplifying assumption has recently been challenged since sociological poll results suggest that real-world agents actually favor diverse neighborhoods. We contribute to the recent endeavor of investigating residential segregation models with realistic agent behavior by studying Jump Schelling Games with agents having a single-peaked utility function. In such games, there are empty nodes in the graph and agents can strategically jump to such nodes to improve their utility. We investigate the existence of equilibria and show that they exist under specific conditions. Contrasting this, we prove that even on simple topologies like paths or rings such stable states are not guaranteed to exist. Regarding the game dynamics, we show that improving response cycles exist independently of the position of the peak in the utility function. Moreover, we show high almost tight bounds on the Price of Anarchy and the Price of Stability with respect to the recently proposed degree of integration, which counts the number of agents with a diverse neighborhood and which serves as a proxy for measuring the segregation strength. Last but not least, we show that computing a beneficial state with high integration is NP-complete and, as a novel conceptual contribution, we also show that it is NP-hard to decide if an equilibrium state can be found via improving response dynamics starting from a given initial state.

Fair Correlation Clustering in Forests

The study of algorithmic fairness received growing attention recently. This stems from the awareness that bias in the input data for machine learning systems may result in discriminatory outputs. For clustering tasks, one of the most central notions of fairness is the formalization by Chierichetti, Kumar, Lattanzi, and Vassilvitskii [NeurIPS 2017]. A clustering is said to be fair, if each cluster has the same distribution of manifestations of a sensitive attribute as the whole input set. This is motivated by various applications where the objects to be clustered have sensitive attributes that should not be over- or underrepresented. We discuss the applicability of this fairness notion to Correlation Clustering. The existing literature on the resulting Fair Correlation Clustering problem either presents approximation algorithms with poor approximation guarantees or severely limits the possible distributions of the sensitive attribute (often only two manifestations with a 1:1 ratio are considered). Our goal is to understand if there is hope for better results in between these two extremes. To this end, we consider restricted graph classes which allow us to characterize the distributions of sensitive attributes for which this form of fairness is tractable from a complexity point of view. While existing work on Fair Correlation Clustering gives approximation algorithms, we focus on exact solutions and investigate whether there are efficiently solvable instances. The unfair version of Correlation Clustering is trivial on forests, but adding fairness creates a surprisingly rich picture of complexities. We give an overview of the distributions and types of forests where Fair Correlation Clustering turns from tractable to intractable. The most surprising insight to us is the fact that the cause of the hardness of Fair Correlation Clustering is not the strictness of the fairness condition.

Theoretical Study of Optimizing Rugged Landscapes with the cGA

Estimation of distribution algorithms (EDAs) provide a distribution - based approach for optimization which adapts its probability distribution during the run of the algorithm. We contribute to the theoretical understanding of EDAs and point out that their distribution approach makes them more suitable to deal with rugged fitness landscapes than classical local search algorithms. Concretely, we make the OneMax function rugged by adding noise to each fitness value. The cGA can nevertheless find solutions with n(1 - \epsilon) many 1s, even for high variance of noise. In contrast to this, RLS and the (1+1) EA, with high probability, only find solutions with n(1/2+o(1)) many 1s, even for noise with small variance.

Deep Distance Sensitivity Oracles

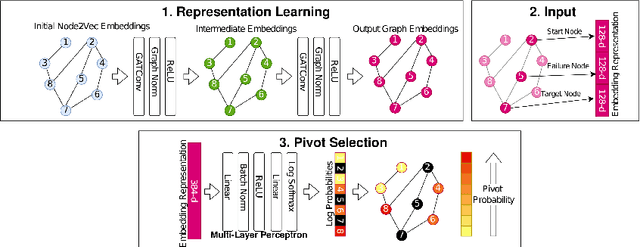
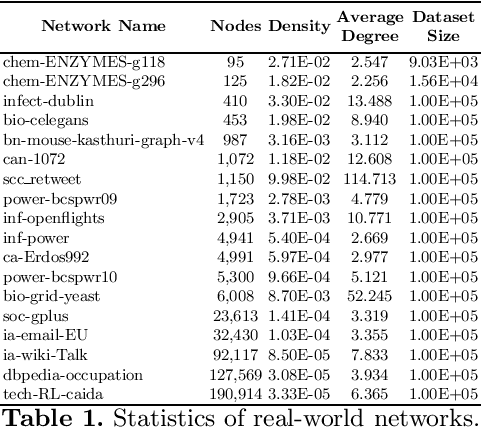
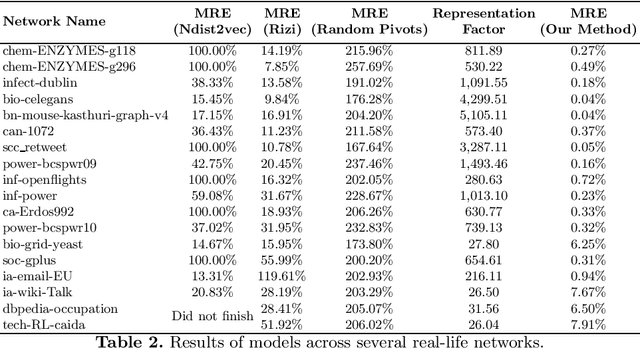
One of the most fundamental graph problems is finding a shortest path from a source to a target node. While in its basic forms the problem has been studied extensively and efficient algorithms are known, it becomes significantly harder as soon as parts of the graph are susceptible to failure. Although one can recompute a shortest replacement path after every outage, this is rather inefficient both in time and/or storage. One way to overcome this problem is to shift computational burden from the queries into a pre-processing step, where a data structure is computed that allows for fast querying of replacement paths, typically referred to as a Distance Sensitivity Oracle (DSO). While DSOs have been extensively studied in the theoretical computer science community, to the best of our knowledge this is the first work to construct DSOs using deep learning techniques. We show how to use deep learning to utilize a combinatorial structure of replacement paths. More specifically, we utilize the combinatorial structure of replacement paths as a concatenation of shortest paths and use deep learning to find the pivot nodes for stitching shortest paths into replacement paths.

Fast Feature Selection with Fairness Constraints

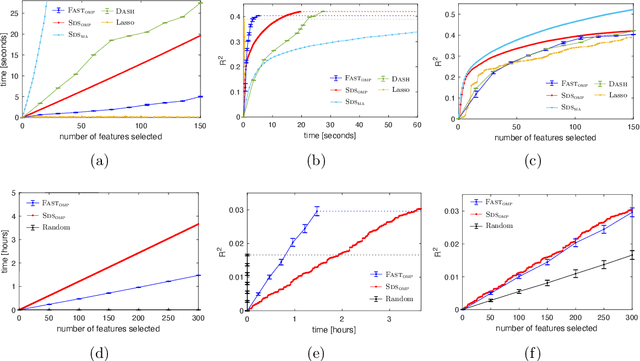
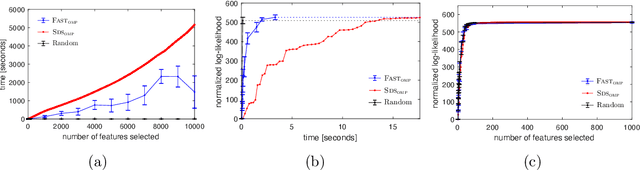
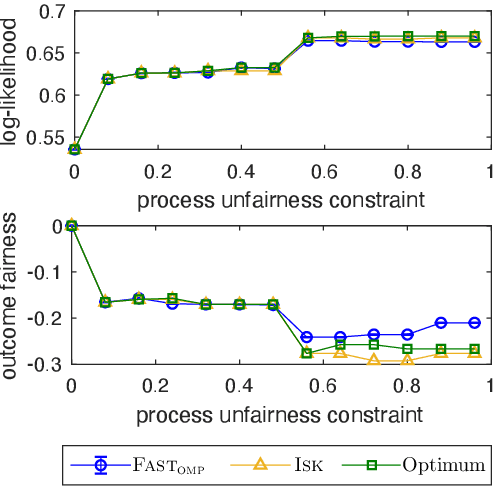
We study the fundamental problem of selecting optimal features for model construction. This problem is computationally challenging on large datasets, even with the use of greedy algorithm variants. To address this challenge, we extend the adaptive query model, recently proposed for the greedy forward selection for submodular functions, to the faster paradigm of Orthogonal Matching Pursuit for non-submodular functions. Our extension also allows the use of downward-closed constraints, which can be used to encode certain fairness criteria into the feature selection process. The proposed algorithm achieves exponentially fast parallel run time in the adaptive query model, scaling much better than prior work. The proposed algorithm also handles certain fairness constraints by design. We prove strong approximation guarantees for the algorithm based on standard assumptions. These guarantees are applicable to many parametric models, including Generalized Linear Models. Finally, we demonstrate empirically that the proposed algorithm competes favorably with state-of-the-art techniques for feature selection, on real-world and synthetic datasets.

What's Wrong with Deep Learning in Tree Search for Combinatorial Optimization

Combinatorial optimization lies at the core of many real-world problems. Especially since the rise of graph neural networks (GNNs), the deep learning community has been developing solvers that derive solutions to NP-hard problems by learning the problem-specific solution structure. However, reproducing the results of these publications proves to be difficult. We make three contributions. First, we present an open-source benchmark suite for the NP-hard Maximum Independent Set problem, in both its weighted and unweighted variants. The suite offers a unified interface to various state-of-the-art traditional and machine learning-based solvers. Second, using our benchmark suite, we conduct an in-depth analysis of the popular guided tree search algorithm by Li et al. [NeurIPS 2018], testing various configurations on small and large synthetic and real-world graphs. By re-implementing their algorithm with a focus on code quality and extensibility, we show that the graph convolution network used in the tree search does not learn a meaningful representation of the solution structure, and can in fact be replaced by random values. Instead, the tree search relies on algorithmic techniques like graph kernelization to find good solutions. Thus, the results from the original publication are not reproducible. Third, we extend the analysis to compare the tree search implementations to other solvers, showing that the classical algorithmic solvers often are faster, while providing solutions of similar quality. Additionally, we analyze a recent solver based on reinforcement learning and observe that for this solver, the GNN is responsible for the competitive solution quality.