ZipNN: Lossless Compression for AI Models

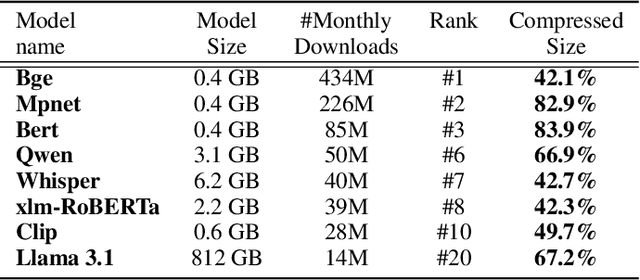
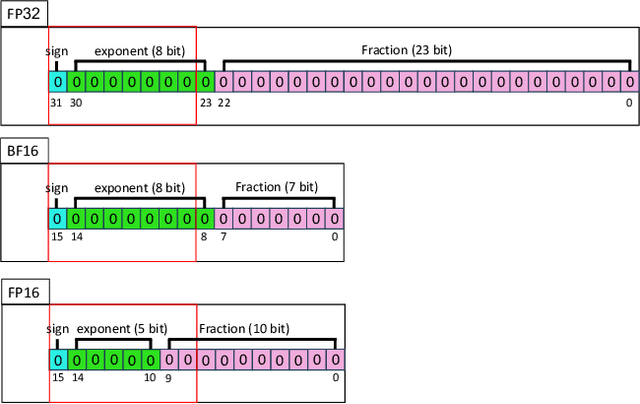
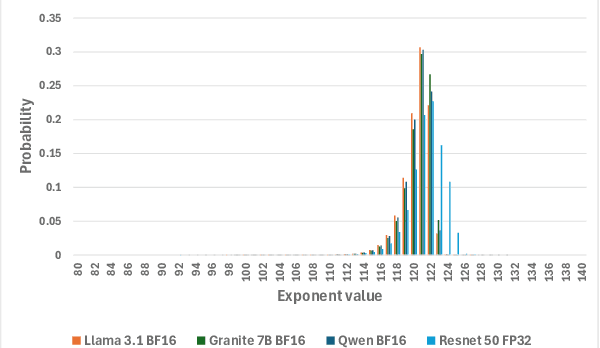
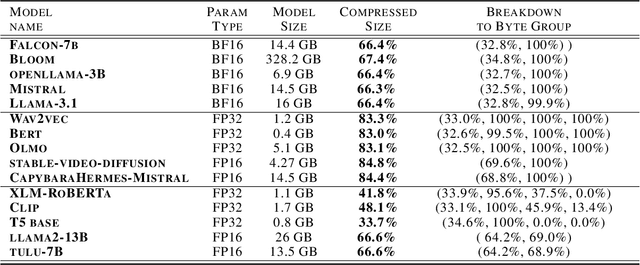
With the growth of model sizes and the scale of their deployment, their sheer size burdens the infrastructure requiring more network and more storage to accommodate these. While there is a vast model compression literature deleting parts of the model weights for faster inference, we investigate a more traditional type of compression - one that represents the model in a compact form and is coupled with a decompression algorithm that returns it to its original form and size - namely lossless compression. We present ZipNN a lossless compression tailored to neural networks. Somewhat surprisingly, we show that specific lossless compression can gain significant network and storage reduction on popular models, often saving 33% and at times reducing over 50% of the model size. We investigate the source of model compressibility and introduce specialized compression variants tailored for models that further increase the effectiveness of compression. On popular models (e.g. Llama 3) ZipNN shows space savings that are over 17% better than vanilla compression while also improving compression and decompression speeds by 62%. We estimate that these methods could save over an ExaByte per month of network traffic downloaded from a large model hub like Hugging Face.

Fast Feature Selection with Fairness Constraints

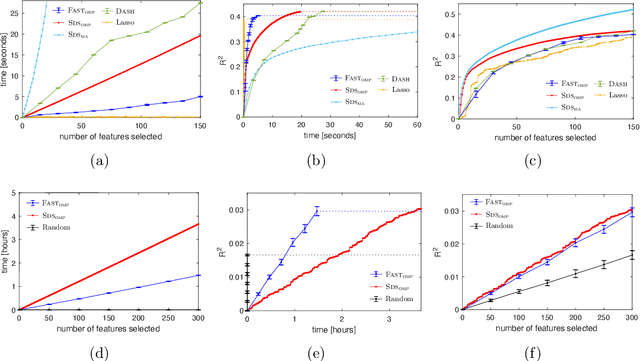
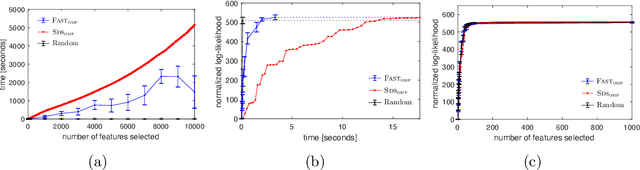
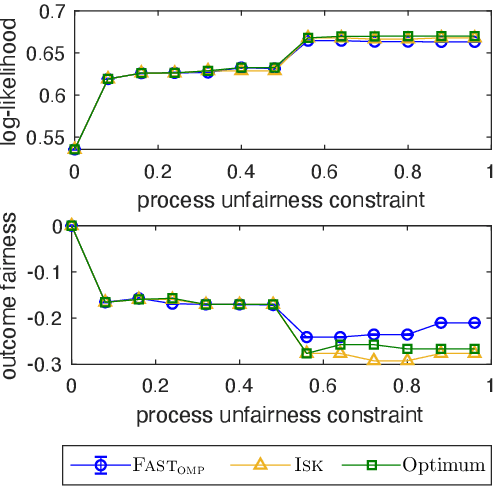
We study the fundamental problem of selecting optimal features for model construction. This problem is computationally challenging on large datasets, even with the use of greedy algorithm variants. To address this challenge, we extend the adaptive query model, recently proposed for the greedy forward selection for submodular functions, to the faster paradigm of Orthogonal Matching Pursuit for non-submodular functions. Our extension also allows the use of downward-closed constraints, which can be used to encode certain fairness criteria into the feature selection process. The proposed algorithm achieves exponentially fast parallel run time in the adaptive query model, scaling much better than prior work. The proposed algorithm also handles certain fairness constraints by design. We prove strong approximation guarantees for the algorithm based on standard assumptions. These guarantees are applicable to many parametric models, including Generalized Linear Models. Finally, we demonstrate empirically that the proposed algorithm competes favorably with state-of-the-art techniques for feature selection, on real-world and synthetic datasets.

Non-Volatile Memory Accelerated Posterior Estimation

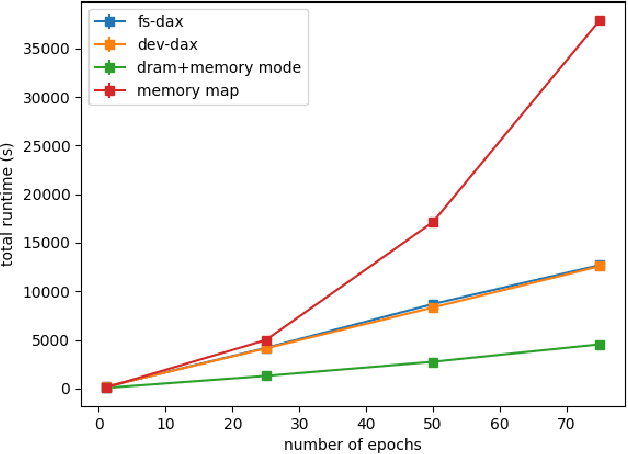
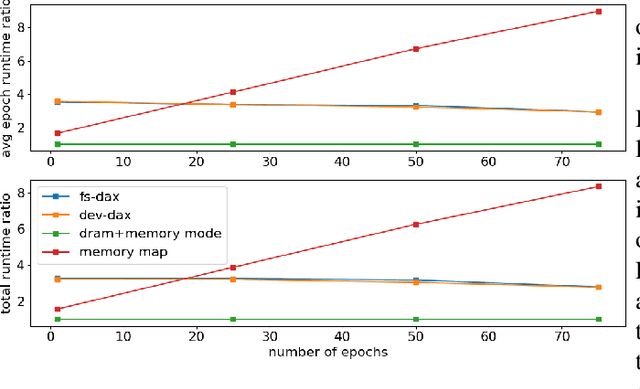
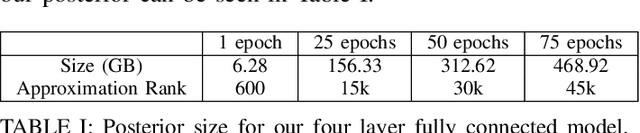
Bayesian inference allows machine learning models to express uncertainty. Current machine learning models use only a single learnable parameter combination when making predictions, and as a result are highly overconfident when their predictions are wrong. To use more learnable parameter combinations efficiently, these samples must be drawn from the posterior distribution. Unfortunately computing the posterior directly is infeasible, so often researchers approximate it with a well known distribution such as a Gaussian. In this paper, we show that through the use of high-capacity persistent storage, models whose posterior distribution was too big to approximate are now feasible, leading to improved predictions in downstream tasks.

Non-Volatile Memory Accelerated Geometric Multi-Scale Resolution Analysis

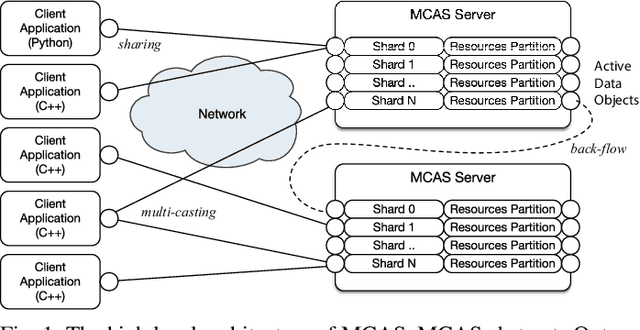
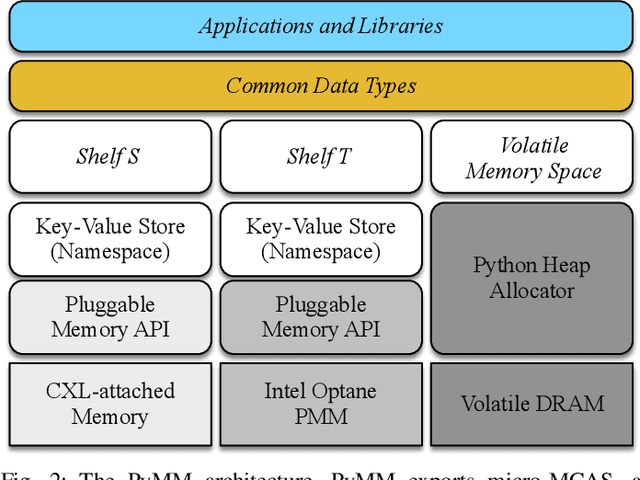
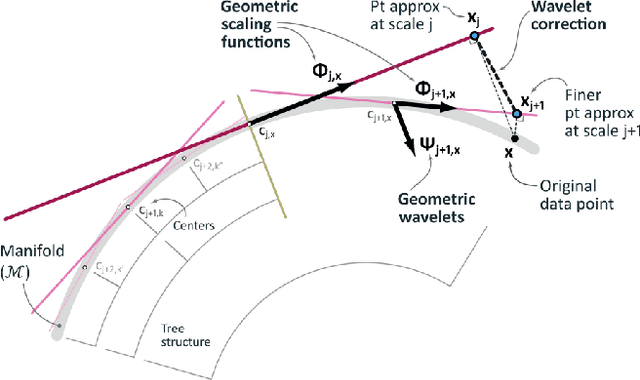
Dimensionality reduction algorithms are standard tools in a researcher's toolbox. Dimensionality reduction algorithms are frequently used to augment downstream tasks such as machine learning, data science, and also are exploratory methods for understanding complex phenomena. For instance, dimensionality reduction is commonly used in Biology as well as Neuroscience to understand data collected from biological subjects. However, dimensionality reduction techniques are limited by the von-Neumann architectures that they execute on. Specifically, data intensive algorithms such as dimensionality reduction techniques often require fast, high capacity, persistent memory which historically hardware has been unable to provide at the same time. In this paper, we present a re-implementation of an existing dimensionality reduction technique called Geometric Multi-Scale Resolution Analysis (GMRA) which has been accelerated via novel persistent memory technology called Memory Centric Active Storage (MCAS). Our implementation uses a specialized version of MCAS called PyMM that provides native support for Python datatypes including NumPy arrays and PyTorch tensors. We compare our PyMM implementation against a DRAM implementation, and show that when data fits in DRAM, PyMM offers competitive runtimes. When data does not fit in DRAM, our PyMM implementation is still able to process the data.