Daniel G. Waddington
Fast Feature Selection with Fairness Constraints
Feb 28, 2022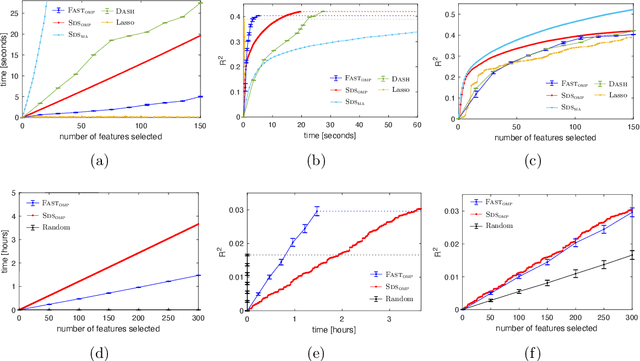
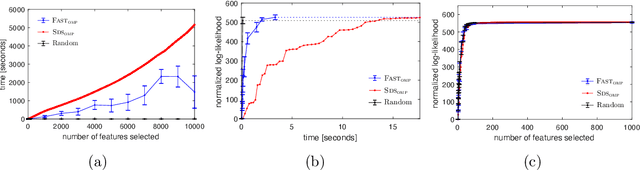
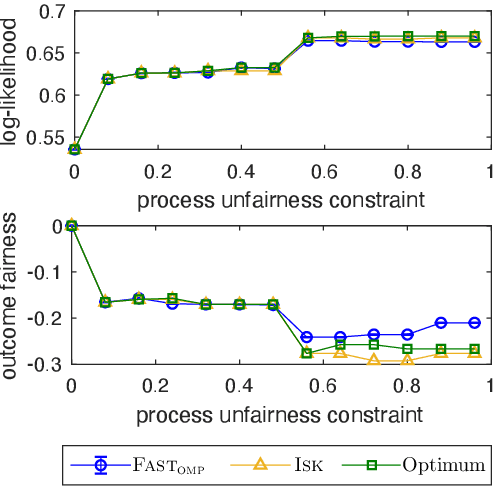
Abstract:We study the fundamental problem of selecting optimal features for model construction. This problem is computationally challenging on large datasets, even with the use of greedy algorithm variants. To address this challenge, we extend the adaptive query model, recently proposed for the greedy forward selection for submodular functions, to the faster paradigm of Orthogonal Matching Pursuit for non-submodular functions. Our extension also allows the use of downward-closed constraints, which can be used to encode certain fairness criteria into the feature selection process. The proposed algorithm achieves exponentially fast parallel run time in the adaptive query model, scaling much better than prior work. The proposed algorithm also handles certain fairness constraints by design. We prove strong approximation guarantees for the algorithm based on standard assumptions. These guarantees are applicable to many parametric models, including Generalized Linear Models. Finally, we demonstrate empirically that the proposed algorithm competes favorably with state-of-the-art techniques for feature selection, on real-world and synthetic datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge