Double Machine Learning for Conditional Moment Restrictions: IV regression, Proximal Causal Learning and Beyond

Solving conditional moment restrictions (CMRs) is a key problem considered in statistics, causal inference, and econometrics, where the aim is to solve for a function of interest that satisfies some conditional moment equalities. Specifically, many techniques for causal inference, such as instrumental variable (IV) regression and proximal causal learning (PCL), are CMR problems. Most CMR estimators use a two-stage approach, where the first-stage estimation is directly plugged into the second stage to estimate the function of interest. However, naively plugging in the first-stage estimator can cause heavy bias in the second stage. This is particularly the case for recently proposed CMR estimators that use deep neural network (DNN) estimators for both stages, where regularisation and overfitting bias is present. We propose DML-CMR, a two-stage CMR estimator that provides an unbiased estimate with fast convergence rate guarantees. We derive a novel learning objective to reduce bias and develop the DML-CMR algorithm following the double/debiased machine learning (DML) framework. We show that our DML-CMR estimator can achieve the minimax optimal convergence rate of $O(N^{-1/2})$ under parameterisation and mild regularity conditions, where $N$ is the sample size. We apply DML-CMR to a range of problems using DNN estimators, including IV regression and proximal causal learning on real-world datasets, demonstrating state-of-the-art performance against existing CMR estimators and algorithms tailored to those problems.

AI Alignment in Medical Imaging: Unveiling Hidden Biases Through Counterfactual Analysis

Machine learning (ML) systems for medical imaging have demonstrated remarkable diagnostic capabilities, but their susceptibility to biases poses significant risks, since biases may negatively impact generalization performance. In this paper, we introduce a novel statistical framework to evaluate the dependency of medical imaging ML models on sensitive attributes, such as demographics. Our method leverages the concept of counterfactual invariance, measuring the extent to which a model's predictions remain unchanged under hypothetical changes to sensitive attributes. We present a practical algorithm that combines conditional latent diffusion models with statistical hypothesis testing to identify and quantify such biases without requiring direct access to counterfactual data. Through experiments on synthetic datasets and large-scale real-world medical imaging datasets, including \textsc{cheXpert} and MIMIC-CXR, we demonstrate that our approach aligns closely with counterfactual fairness principles and outperforms standard baselines. This work provides a robust tool to ensure that ML diagnostic systems generalize well, e.g., across demographic groups, offering a critical step towards AI safety in healthcare. Code: https://github.com/Neferpitou3871/AI-Alignment-Medical-Imaging.

When Should We Orchestrate Multiple Agents?

Strategies for orchestrating the interactions between multiple agents, both human and artificial, can wildly overestimate performance and underestimate the cost of orchestration. We design a framework to orchestrate agents under realistic conditions, such as inference costs or availability constraints. We show theoretically that orchestration is only effective if there are performance or cost differentials between agents. We then empirically demonstrate how orchestration between multiple agents can be helpful for selecting agents in a simulated environment, picking a learning strategy in the infamous Rogers' Paradox from social science, and outsourcing tasks to other agents during a question-answer task in a user study.

Learning Decision Policies with Instrumental Variables through Double Machine Learning

A common issue in learning decision-making policies in data-rich settings is spurious correlations in the offline dataset, which can be caused by hidden confounders. Instrumental variable (IV) regression, which utilises a key unconfounded variable known as the instrument, is a standard technique for learning causal relationships between confounded action, outcome, and context variables. Most recent IV regression algorithms use a two-stage approach, where a deep neural network (DNN) estimator learnt in the first stage is directly plugged into the second stage, in which another DNN is used to estimate the causal effect. Naively plugging the estimator can cause heavy bias in the second stage, especially when regularisation bias is present in the first stage estimator. We propose DML-IV, a non-linear IV regression method that reduces the bias in two-stage IV regressions and effectively learns high-performing policies. We derive a novel learning objective to reduce bias and design the DML-IV algorithm following the double/debiased machine learning (DML) framework. The learnt DML-IV estimator has strong convergence rate and $O(N^{-1/2})$ suboptimality guarantees that match those when the dataset is unconfounded. DML-IV outperforms state-of-the-art IV regression methods on IV regression benchmarks and learns high-performing policies in the presence of instruments.

Doubly Robust Structure Identification from Temporal Data

Learning the causes of time-series data is a fundamental task in many applications, spanning from finance to earth sciences or bio-medical applications. Common approaches for this task are based on vector auto-regression, and they do not take into account unknown confounding between potential causes. However, in settings with many potential causes and noisy data, these approaches may be substantially biased. Furthermore, potential causes may be correlated in practical applications. Moreover, existing algorithms often do not work with cyclic data. To address these challenges, we propose a new doubly robust method for Structure Identification from Temporal Data ( SITD ). We provide theoretical guarantees, showing that our method asymptotically recovers the true underlying causal structure. Our analysis extends to cases where the potential causes have cycles and they may be confounded. We further perform extensive experiments to showcase the superior performance of our method.

Diffusion Based Causal Representation Learning

Causal reasoning can be considered a cornerstone of intelligent systems. Having access to an underlying causal graph comes with the promise of cause-effect estimation and the identification of efficient and safe interventions. However, learning causal representations remains a major challenge, due to the complexity of many real-world systems. Previous works on causal representation learning have mostly focused on Variational Auto-Encoders (VAE). These methods only provide representations from a point estimate, and they are unsuitable to handle high dimensions. To overcome these problems, we proposed a new Diffusion-based Causal Representation Learning (DCRL) algorithm. This algorithm uses diffusion-based representations for causal discovery. DCRL offers access to infinite dimensional latent codes, which encode different levels of information in the latent code. In a first proof of principle, we investigate the use of DCRL for causal representation learning. We further demonstrate experimentally that this approach performs comparably well in identifying the causal structure and causal variables.

DRCFS: Doubly Robust Causal Feature Selection

Knowing the features of a complex system that are highly relevant to a particular target variable is of fundamental interest in many areas of science. Existing approaches are often limited to linear settings, sometimes lack guarantees, and in most cases, do not scale to the problem at hand, in particular to images. We propose DRCFS, a doubly robust feature selection method for identifying the causal features even in nonlinear and high dimensional settings. We provide theoretical guarantees, illustrate necessary conditions for our assumptions, and perform extensive experiments across a wide range of simulated and semi-synthetic datasets. DRCFS significantly outperforms existing state-of-the-art methods, selecting robust features even in challenging highly non-linear and high-dimensional problems.

Optimal Transport for Correctional Learning

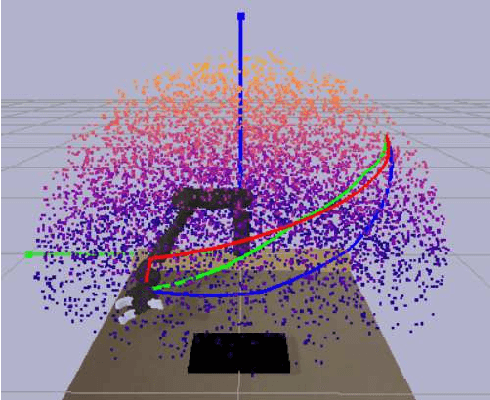
The contribution of this paper is a generalized formulation of correctional learning using optimal transport, which is about how to optimally transport one mass distribution to another. Correctional learning is a framework developed to enhance the accuracy of parameter estimation processes by means of a teacher-student approach. In this framework, an expert agent, referred to as the teacher, modifies the data used by a learning agent, known as the student, to improve its estimation process. The objective of the teacher is to alter the data such that the student's estimation error is minimized, subject to a fixed intervention budget. Compared to existing formulations of correctional learning, our novel optimal transport approach provides several benefits. It allows for the estimation of more complex characteristics as well as the consideration of multiple intervention policies for the teacher. We evaluate our approach on two theoretical examples, and on a human-robot interaction application in which the teacher's role is to improve the robots performance in an inverse reinforcement learning setting.

Learning Counterfactually Invariant Predictors

We propose a method to learn predictors that are invariant under counterfactual changes of certain covariates. This method is useful when the prediction target is causally influenced by covariates that should not affect the predictor output. For instance, an object recognition model may be influenced by position, orientation, or scale of the object itself. We address the problem of training predictors that are explicitly counterfactually invariant to changes of such covariates. We propose a model-agnostic regularization term based on conditional kernel mean embeddings, to enforce counterfactual invariance during training. We prove the soundness of our method, which can handle mixed categorical and continuous multi-variate attributes. Empirical results on synthetic and real-world data demonstrate the efficacy of our method in a variety of settings.

Fast Feature Selection with Fairness Constraints

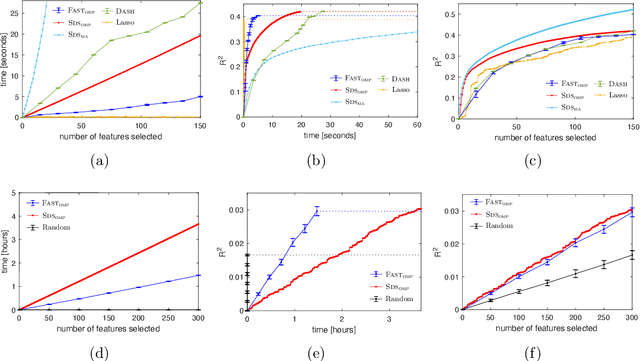
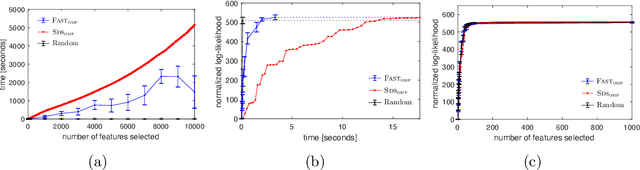
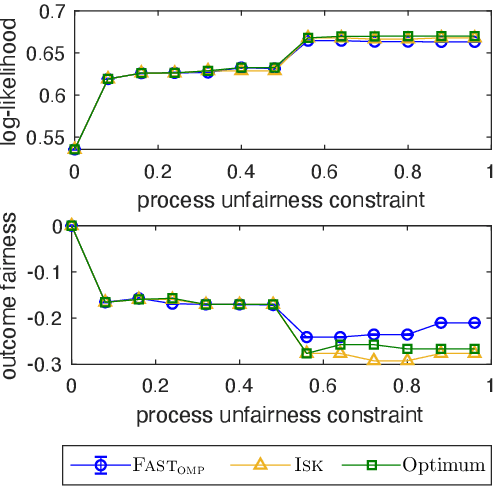
We study the fundamental problem of selecting optimal features for model construction. This problem is computationally challenging on large datasets, even with the use of greedy algorithm variants. To address this challenge, we extend the adaptive query model, recently proposed for the greedy forward selection for submodular functions, to the faster paradigm of Orthogonal Matching Pursuit for non-submodular functions. Our extension also allows the use of downward-closed constraints, which can be used to encode certain fairness criteria into the feature selection process. The proposed algorithm achieves exponentially fast parallel run time in the adaptive query model, scaling much better than prior work. The proposed algorithm also handles certain fairness constraints by design. We prove strong approximation guarantees for the algorithm based on standard assumptions. These guarantees are applicable to many parametric models, including Generalized Linear Models. Finally, we demonstrate empirically that the proposed algorithm competes favorably with state-of-the-art techniques for feature selection, on real-world and synthetic datasets.