When Should We Orchestrate Multiple Agents?

Strategies for orchestrating the interactions between multiple agents, both human and artificial, can wildly overestimate performance and underestimate the cost of orchestration. We design a framework to orchestrate agents under realistic conditions, such as inference costs or availability constraints. We show theoretically that orchestration is only effective if there are performance or cost differentials between agents. We then empirically demonstrate how orchestration between multiple agents can be helpful for selecting agents in a simulated environment, picking a learning strategy in the infamous Rogers' Paradox from social science, and outsourcing tasks to other agents during a question-answer task in a user study.

Large Language Models Must Be Taught to Know What They Don't Know

When using large language models (LLMs) in high-stakes applications, we need to know when we can trust their predictions. Some works argue that prompting high-performance LLMs is sufficient to produce calibrated uncertainties, while others introduce sampling methods that can be prohibitively expensive. In this work, we first argue that prompting on its own is insufficient to achieve good calibration and then show that fine-tuning on a small dataset of correct and incorrect answers can create an uncertainty estimate with good generalization and small computational overhead. We show that a thousand graded examples are sufficient to outperform baseline methods and that training through the features of a model is necessary for good performance and tractable for large open-source models when using LoRA. We also investigate the mechanisms that enable reliable LLM uncertainty estimation, finding that many models can be used as general-purpose uncertainty estimators, applicable not just to their own uncertainties but also the uncertainty of other models. Lastly, we show that uncertainty estimates inform human use of LLMs in human-AI collaborative settings through a user study.

Function-Space Regularization in Neural Networks: A Probabilistic Perspective

Parameter-space regularization in neural network optimization is a fundamental tool for improving generalization. However, standard parameter-space regularization methods make it challenging to encode explicit preferences about desired predictive functions into neural network training. In this work, we approach regularization in neural networks from a probabilistic perspective and show that by viewing parameter-space regularization as specifying an empirical prior distribution over the model parameters, we can derive a probabilistically well-motivated regularization technique that allows explicitly encoding information about desired predictive functions into neural network training. This method -- which we refer to as function-space empirical Bayes (FSEB) -- includes both parameter- and function-space regularization, is mathematically simple, easy to implement, and incurs only minimal computational overhead compared to standard regularization techniques. We evaluate the utility of this regularization technique empirically and demonstrate that the proposed method leads to near-perfect semantic shift detection, highly-calibrated predictive uncertainty estimates, successful task adaption from pre-trained models, and improved generalization under covariate shift.

Should We Learn Most Likely Functions or Parameters?

Standard regularized training procedures correspond to maximizing a posterior distribution over parameters, known as maximum a posteriori (MAP) estimation. However, model parameters are of interest only insomuch as they combine with the functional form of a model to provide a function that can make good predictions. Moreover, the most likely parameters under the parameter posterior do not generally correspond to the most likely function induced by the parameter posterior. In fact, we can re-parametrize a model such that any setting of parameters can maximize the parameter posterior. As an alternative, we investigate the benefits and drawbacks of directly estimating the most likely function implied by the model and the data. We show that this procedure leads to pathological solutions when using neural networks and prove conditions under which the procedure is well-behaved, as well as a scalable approximation. Under these conditions, we find that function-space MAP estimation can lead to flatter minima, better generalization, and improved robustness to overfitting.

PAC-Bayes Compression Bounds So Tight That They Can Explain Generalization

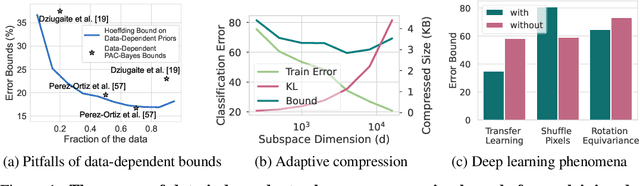
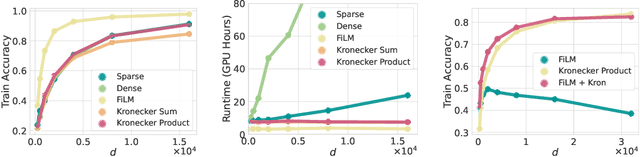
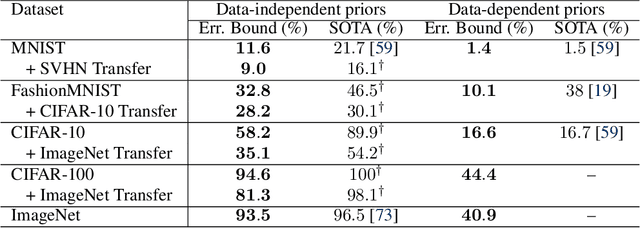
While there has been progress in developing non-vacuous generalization bounds for deep neural networks, these bounds tend to be uninformative about why deep learning works. In this paper, we develop a compression approach based on quantizing neural network parameters in a linear subspace, profoundly improving on previous results to provide state-of-the-art generalization bounds on a variety of tasks, including transfer learning. We use these tight bounds to better understand the role of model size, equivariance, and the implicit biases of optimization, for generalization in deep learning. Notably, we find large models can be compressed to a much greater extent than previously known, encapsulating Occam's razor. We also argue for data-independent bounds in explaining generalization.

Pre-Train Your Loss: Easy Bayesian Transfer Learning with Informative Priors

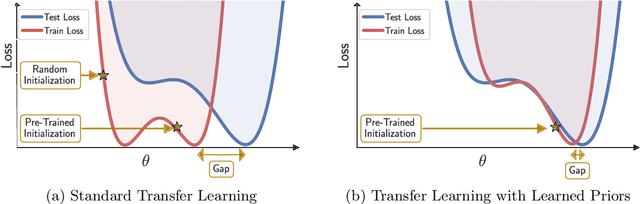
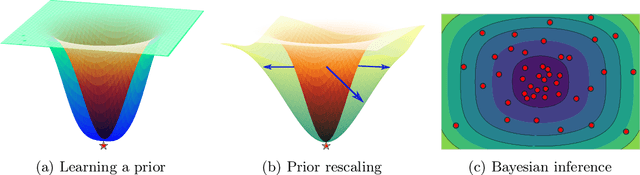
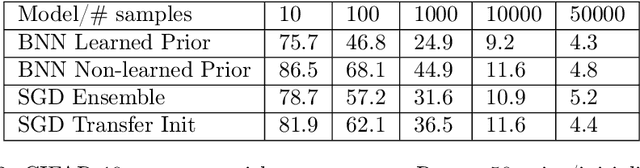
Deep learning is increasingly moving towards a transfer learning paradigm whereby large foundation models are fine-tuned on downstream tasks, starting from an initialization learned on the source task. But an initialization contains relatively little information about the source task. Instead, we show that we can learn highly informative posteriors from the source task, through supervised or self-supervised approaches, which then serve as the basis for priors that modify the whole loss surface on the downstream task. This simple modular approach enables significant performance gains and more data-efficient learning on a variety of downstream classification and segmentation tasks, serving as a drop-in replacement for standard pre-training strategies. These highly informative priors also can be saved for future use, similar to pre-trained weights, and stand in contrast to the zero-mean isotropic uninformative priors that are typically used in Bayesian deep learning.

On Uncertainty, Tempering, and Data Augmentation in Bayesian Classification

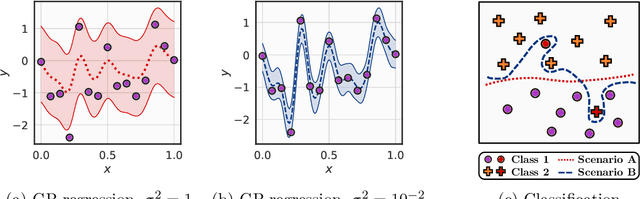
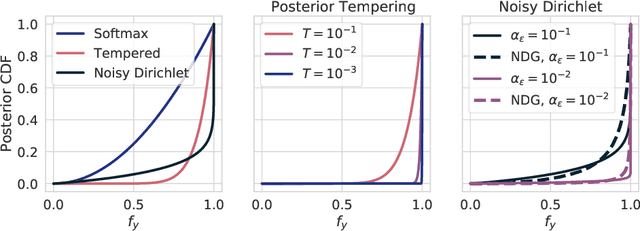
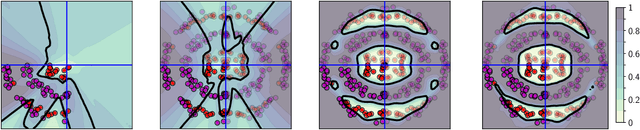
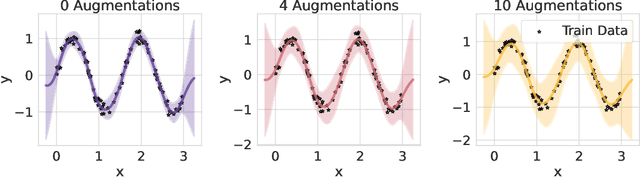
Aleatoric uncertainty captures the inherent randomness of the data, such as measurement noise. In Bayesian regression, we often use a Gaussian observation model, where we control the level of aleatoric uncertainty with a noise variance parameter. By contrast, for Bayesian classification we use a categorical distribution with no mechanism to represent our beliefs about aleatoric uncertainty. Our work shows that explicitly accounting for aleatoric uncertainty significantly improves the performance of Bayesian neural networks. We note that many standard benchmarks, such as CIFAR, have essentially no aleatoric uncertainty. Moreover, we show data augmentation in approximate inference has the effect of softening the likelihood, leading to underconfidence and profoundly misrepresenting our honest beliefs about aleatoric uncertainty. Accordingly, we find that a cold posterior, tempered by a power greater than one, often more honestly reflects our beliefs about aleatoric uncertainty than no tempering -- providing an explicit link between data augmentation and cold posteriors. We show that we can match or exceed the performance of posterior tempering by using a Dirichlet observation model, where we explicitly control the level of aleatoric uncertainty, without any need for tempering.

When are Iterative Gaussian Processes Reliably Accurate?

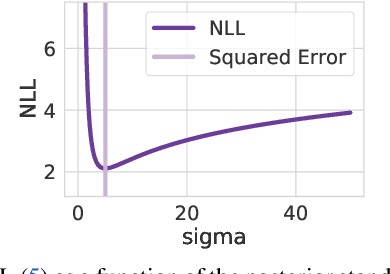
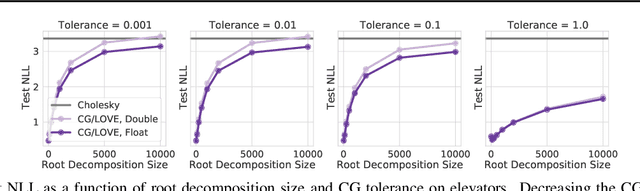
While recent work on conjugate gradient methods and Lanczos decompositions have achieved scalable Gaussian process inference with highly accurate point predictions, in several implementations these iterative methods appear to struggle with numerical instabilities in learning kernel hyperparameters, and poor test likelihoods. By investigating CG tolerance, preconditioner rank, and Lanczos decomposition rank, we provide a particularly simple prescription to correct these issues: we recommend that one should use a small CG tolerance ($\epsilon \leq 0.01$) and a large root decomposition size ($r \geq 5000$). Moreover, we show that L-BFGS-B is a compelling optimizer for Iterative GPs, achieving convergence with fewer gradient updates.

A Simple and Fast Baseline for Tuning Large XGBoost Models

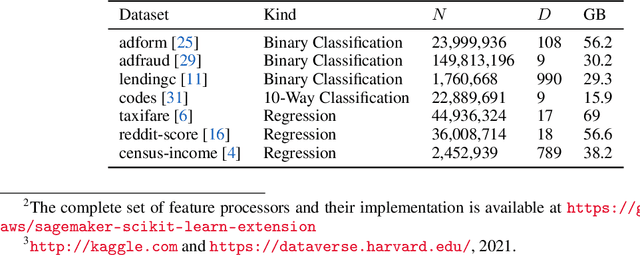
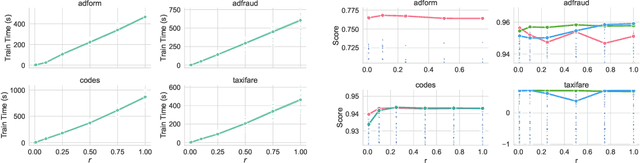
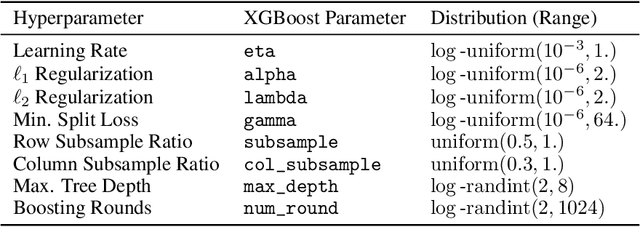
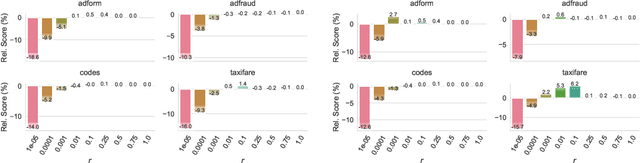
XGBoost, a scalable tree boosting algorithm, has proven effective for many prediction tasks of practical interest, especially using tabular datasets. Hyperparameter tuning can further improve the predictive performance, but unlike neural networks, full-batch training of many models on large datasets can be time consuming. Owing to the discovery that (i) there is a strong linear relation between dataset size & training time, (ii) XGBoost models satisfy the ranking hypothesis, and (iii) lower-fidelity models can discover promising hyperparameter configurations, we show that uniform subsampling makes for a simple yet fast baseline to speed up the tuning of large XGBoost models using multi-fidelity hyperparameter optimization with data subsets as the fidelity dimension. We demonstrate the effectiveness of this baseline on large-scale tabular datasets ranging from $15-70\mathrm{GB}$ in size.

SKIing on Simplices: Kernel Interpolation on the Permutohedral Lattice for Scalable Gaussian Processes

State-of-the-art methods for scalable Gaussian processes use iterative algorithms, requiring fast matrix vector multiplies (MVMs) with the covariance kernel. The Structured Kernel Interpolation (SKI) framework accelerates these MVMs by performing efficient MVMs on a grid and interpolating back to the original space. In this work, we develop a connection between SKI and the permutohedral lattice used for high-dimensional fast bilateral filtering. Using a sparse simplicial grid instead of a dense rectangular one, we can perform GP inference exponentially faster in the dimension than SKI. Our approach, Simplex-GP, enables scaling SKI to high dimensions, while maintaining strong predictive performance. We additionally provide a CUDA implementation of Simplex-GP, which enables significant GPU acceleration of MVM based inference.