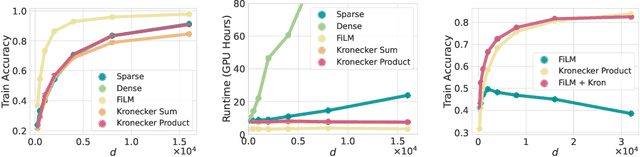
Searching for Efficient Linear Layers over a Continuous Space of Structured Matrices

Dense linear layers are the dominant computational bottleneck in large neural networks, presenting a critical need for more efficient alternatives. Previous efforts focused on a small number of hand-crafted structured matrices and neglected to investigate whether these structures can surpass dense layers in terms of compute-optimal scaling laws when both the model size and training examples are optimally allocated. In this work, we present a unifying framework that enables searching among all linear operators expressible via an Einstein summation. This framework encompasses many previously proposed structures, such as low-rank, Kronecker, Tensor-Train, Block Tensor-Train (BTT), and Monarch, along with many novel structures. To analyze the framework, we develop a taxonomy of all such operators based on their computational and algebraic properties and show that differences in the compute-optimal scaling laws are mostly governed by a small number of variables that we introduce. Namely, a small $\omega$ (which measures parameter sharing) and large $\psi$ (which measures the rank) reliably led to better scaling laws. Guided by the insight that full-rank structures that maximize parameters per unit of compute perform the best, we propose BTT-MoE, a novel Mixture-of-Experts (MoE) architecture obtained by sparsifying computation in the BTT structure. In contrast to the standard sparse MoE for each entire feed-forward network, BTT-MoE learns an MoE in every single linear layer of the model, including the projection matrices in the attention blocks. We find BTT-MoE provides a substantial compute-efficiency gain over dense layers and standard MoE.

Compute Better Spent: Replacing Dense Layers with Structured Matrices

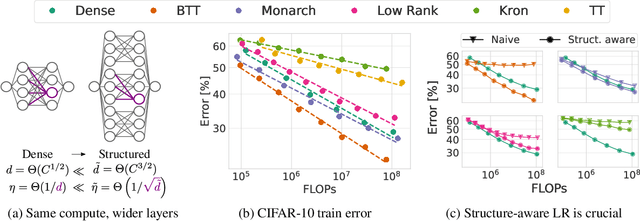
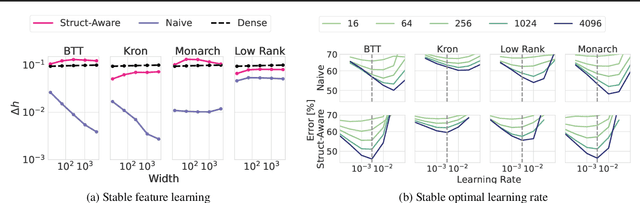
Dense linear layers are the dominant computational bottleneck in foundation models. Identifying more efficient alternatives to dense matrices has enormous potential for building more compute-efficient models, as exemplified by the success of convolutional networks in the image domain. In this work, we systematically explore structured matrices as replacements for dense matrices. We show that different structures often require drastically different initialization scales and learning rates, which are crucial to performance, especially as models scale. Using insights from the Maximal Update Parameterization, we determine the optimal scaling for initialization and learning rates of these unconventional layers. Finally, we measure the scaling laws of different structures to compare how quickly their performance improves with compute. We propose a novel matrix family containing Monarch matrices, the Block Tensor-Train (BTT), which we show performs better than dense matrices for the same compute on multiple tasks. On CIFAR-10/100 with augmentation, BTT achieves exponentially lower training loss than dense when training MLPs and ViTs. BTT matches dense ViT-S/32 performance on ImageNet-1k with 3.8 times less compute and is more efficient than dense for training small GPT-2 language models.

CoLA: Exploiting Compositional Structure for Automatic and Efficient Numerical Linear Algebra

Many areas of machine learning and science involve large linear algebra problems, such as eigendecompositions, solving linear systems, computing matrix exponentials, and trace estimation. The matrices involved often have Kronecker, convolutional, block diagonal, sum, or product structure. In this paper, we propose a simple but general framework for large-scale linear algebra problems in machine learning, named CoLA (Compositional Linear Algebra). By combining a linear operator abstraction with compositional dispatch rules, CoLA automatically constructs memory and runtime efficient numerical algorithms. Moreover, CoLA provides memory efficient automatic differentiation, low precision computation, and GPU acceleration in both JAX and PyTorch, while also accommodating new objects, operations, and rules in downstream packages via multiple dispatch. CoLA can accelerate many algebraic operations, while making it easy to prototype matrix structures and algorithms, providing an appealing drop-in tool for virtually any computational effort that requires linear algebra. We showcase its efficacy across a broad range of applications, including partial differential equations, Gaussian processes, equivariant model construction, and unsupervised learning.

Simple and Fast Group Robustness by Automatic Feature Reweighting

A major challenge to out-of-distribution generalization is reliance on spurious features -- patterns that are predictive of the class label in the training data distribution, but not causally related to the target. Standard methods for reducing the reliance on spurious features typically assume that we know what the spurious feature is, which is rarely true in the real world. Methods that attempt to alleviate this limitation are complex, hard to tune, and lead to a significant computational overhead compared to standard training. In this paper, we propose Automatic Feature Reweighting (AFR), an extremely simple and fast method for updating the model to reduce the reliance on spurious features. AFR retrains the last layer of a standard ERM-trained base model with a weighted loss that emphasizes the examples where the ERM model predicts poorly, automatically upweighting the minority group without group labels. With this simple procedure, we improve upon the best reported results among competing methods trained without spurious attributes on several vision and natural language classification benchmarks, using only a fraction of their compute.

A Stable and Scalable Method for Solving Initial Value PDEs with Neural Networks

Unlike conventional grid and mesh based methods for solving partial differential equations (PDEs), neural networks have the potential to break the curse of dimensionality, providing approximate solutions to problems where using classical solvers is difficult or impossible. While global minimization of the PDE residual over the network parameters works well for boundary value problems, catastrophic forgetting impairs the applicability of this approach to initial value problems (IVPs). In an alternative local-in-time approach, the optimization problem can be converted into an ordinary differential equation (ODE) on the network parameters and the solution propagated forward in time; however, we demonstrate that current methods based on this approach suffer from two key issues. First, following the ODE produces an uncontrolled growth in the conditioning of the problem, ultimately leading to unacceptably large numerical errors. Second, as the ODE methods scale cubically with the number of model parameters, they are restricted to small neural networks, significantly limiting their ability to represent intricate PDE initial conditions and solutions. Building on these insights, we develop Neural IVP, an ODE based IVP solver which prevents the network from getting ill-conditioned and runs in time linear in the number of parameters, enabling us to evolve the dynamics of challenging PDEs with neural networks.

PAC-Bayes Compression Bounds So Tight That They Can Explain Generalization

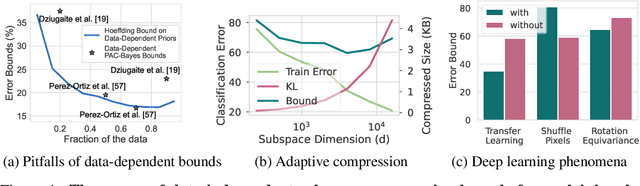
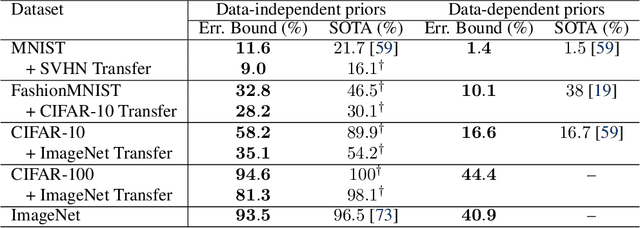
While there has been progress in developing non-vacuous generalization bounds for deep neural networks, these bounds tend to be uninformative about why deep learning works. In this paper, we develop a compression approach based on quantizing neural network parameters in a linear subspace, profoundly improving on previous results to provide state-of-the-art generalization bounds on a variety of tasks, including transfer learning. We use these tight bounds to better understand the role of model size, equivariance, and the implicit biases of optimization, for generalization in deep learning. Notably, we find large models can be compressed to a much greater extent than previously known, encapsulating Occam's razor. We also argue for data-independent bounds in explaining generalization.

Low-Precision Arithmetic for Fast Gaussian Processes

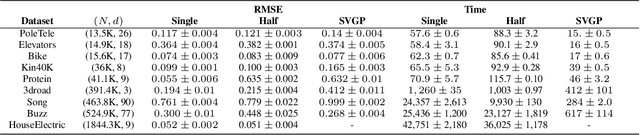
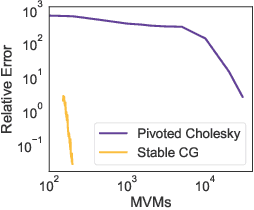
Low-precision arithmetic has had a transformative effect on the training of neural networks, reducing computation, memory and energy requirements. However, despite its promise, low-precision arithmetic has received little attention for Gaussian processes (GPs), largely because GPs require sophisticated linear algebra routines that are unstable in low-precision. We study the different failure modes that can occur when training GPs in half precision. To circumvent these failure modes, we propose a multi-faceted approach involving conjugate gradients with re-orthogonalization, mixed precision, and preconditioning. Our approach significantly improves the numerical stability and practical performance of conjugate gradients in low-precision over a wide range of settings, enabling GPs to train on $1.8$ million data points in $10$ hours on a single GPU, without any sparse approximations.

On the Normalizing Constant of the Continuous Categorical Distribution

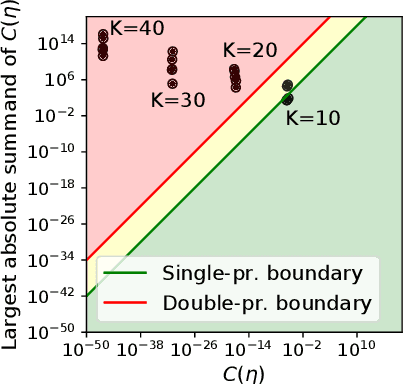
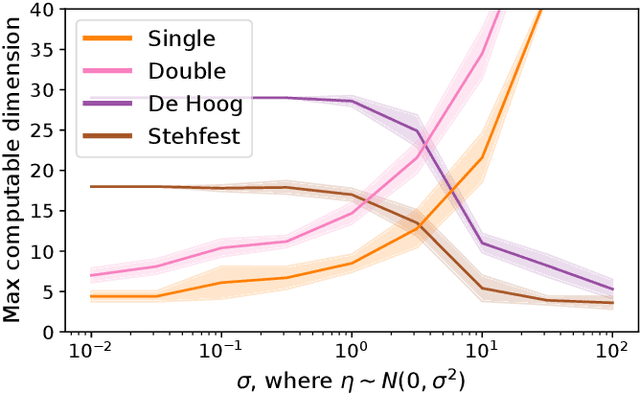
Probability distributions supported on the simplex enjoy a wide range of applications across statistics and machine learning. Recently, a novel family of such distributions has been discovered: the continuous categorical. This family enjoys remarkable mathematical simplicity; its density function resembles that of the Dirichlet distribution, but with a normalizing constant that can be written in closed form using elementary functions only. In spite of this mathematical simplicity, our understanding of the normalizing constant remains far from complete. In this work, we characterize the numerical behavior of the normalizing constant and we present theoretical and methodological advances that can, in turn, help to enable broader applications of the continuous categorical distribution. Our code is available at https://github.com/cunningham-lab/cb_and_cc/.

Bias-Free Scalable Gaussian Processes via Randomized Truncations

Scalable Gaussian Process methods are computationally attractive, yet introduce modeling biases that require rigorous study. This paper analyzes two common techniques: early truncated conjugate gradients (CG) and random Fourier features (RFF). We find that both methods introduce a systematic bias on the learned hyperparameters: CG tends to underfit while RFF tends to overfit. We address these issues using randomized truncation estimators that eliminate bias in exchange for increased variance. In the case of RFF, we show that the bias-to-variance conversion is indeed a trade-off: the additional variance proves detrimental to optimization. However, in the case of CG, our unbiased learning procedure meaningfully outperforms its biased counterpart with minimal additional computation.

Invertible Gaussian Reparameterization: Revisiting the Gumbel-Softmax

The Gumbel-Softmax is a continuous distribution over the simplex that is often used as a relaxation of discrete distributions. Because it can be readily interpreted and easily reparameterized, it enjoys widespread use. Unfortunately, we show that the cost of this aesthetic interpretability is material: the temperature hyperparameter must be set too high, KL estimates are noisy, and as a result, performance suffers. We circumvent the previous issues by proposing a much simpler and more flexible reparameterizable family of distributions that transforms Gaussian noise into a one-hot approximation through an invertible function. This invertible function is composed of a modified softmax and can incorporate diverse transformations that serve different specific purposes. For example, the stick-breaking procedure allows us to extend the reparameterization trick to distributions with countably infinite support, or normalizing flows let us increase the flexibility of the distribution. Our construction improves numerical stability and outperforms the Gumbel-Softmax in a variety of experiments while generating samples that are closer to their discrete counterparts and achieving lower-variance gradients.