Low-Precision Arithmetic for Fast Gaussian Processes
Paper and Code
Jul 14, 2022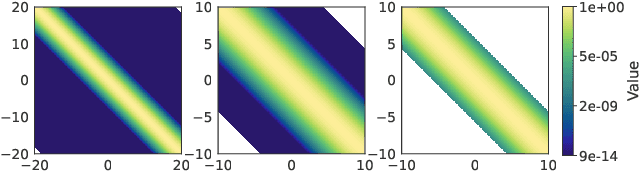
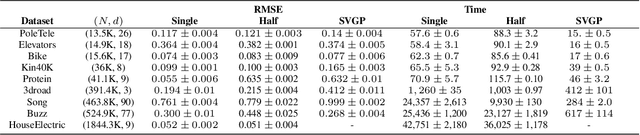

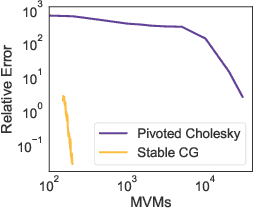
Low-precision arithmetic has had a transformative effect on the training of neural networks, reducing computation, memory and energy requirements. However, despite its promise, low-precision arithmetic has received little attention for Gaussian processes (GPs), largely because GPs require sophisticated linear algebra routines that are unstable in low-precision. We study the different failure modes that can occur when training GPs in half precision. To circumvent these failure modes, we propose a multi-faceted approach involving conjugate gradients with re-orthogonalization, mixed precision, and preconditioning. Our approach significantly improves the numerical stability and practical performance of conjugate gradients in low-precision over a wide range of settings, enabling GPs to train on $1.8$ million data points in $10$ hours on a single GPU, without any sparse approximations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge