Data Augmentation for Compositional Data: Advancing Predictive Models of the Microbiome

Data augmentation plays a key role in modern machine learning pipelines. While numerous augmentation strategies have been studied in the context of computer vision and natural language processing, less is known for other data modalities. Our work extends the success of data augmentation to compositional data, i.e., simplex-valued data, which is of particular interest in the context of the human microbiome. Drawing on key principles from compositional data analysis, such as the Aitchison geometry of the simplex and subcompositions, we define novel augmentation strategies for this data modality. Incorporating our data augmentations into standard supervised learning pipelines results in consistent performance gains across a wide range of standard benchmark datasets. In particular, we set a new state-of-the-art for key disease prediction tasks including colorectal cancer, type 2 diabetes, and Crohn's disease. In addition, our data augmentations enable us to define a novel contrastive learning model, which improves on previous representation learning approaches for microbiome compositional data. Our code is available at https://github.com/cunningham-lab/AugCoDa.

On the Normalizing Constant of the Continuous Categorical Distribution

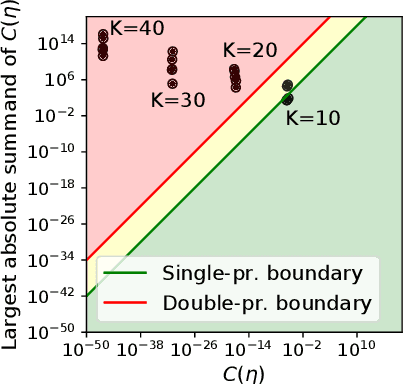
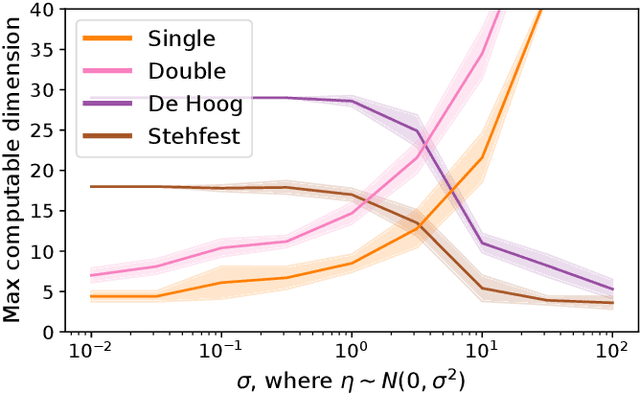
Probability distributions supported on the simplex enjoy a wide range of applications across statistics and machine learning. Recently, a novel family of such distributions has been discovered: the continuous categorical. This family enjoys remarkable mathematical simplicity; its density function resembles that of the Dirichlet distribution, but with a normalizing constant that can be written in closed form using elementary functions only. In spite of this mathematical simplicity, our understanding of the normalizing constant remains far from complete. In this work, we characterize the numerical behavior of the normalizing constant and we present theoretical and methodological advances that can, in turn, help to enable broader applications of the continuous categorical distribution. Our code is available at https://github.com/cunningham-lab/cb_and_cc/.

Uses and Abuses of the Cross-Entropy Loss: Case Studies in Modern Deep Learning

Modern deep learning is primarily an experimental science, in which empirical advances occasionally come at the expense of probabilistic rigor. Here we focus on one such example; namely the use of the categorical cross-entropy loss to model data that is not strictly categorical, but rather takes values on the simplex. This practice is standard in neural network architectures with label smoothing and actor-mimic reinforcement learning, amongst others. Drawing on the recently discovered continuous-categorical distribution, we propose probabilistically-inspired alternatives to these models, providing an approach that is more principled and theoretically appealing. Through careful experimentation, including an ablation study, we identify the potential for outperformance in these models, thereby highlighting the importance of a proper probabilistic treatment, as well as illustrating some of the failure modes thereof.

The continuous categorical: a novel simplex-valued exponential family

Simplex-valued data appear throughout statistics and machine learning, for example in the context of transfer learning and compression of deep networks. Existing models for this class of data rely on the Dirichlet distribution or other related loss functions; here we show these standard choices suffer systematically from a number of limitations, including bias and numerical issues that frustrate the use of flexible network models upstream of these distributions. We resolve these limitations by introducing a novel exponential family of distributions for modeling simplex-valued data - the continuous categorical, which arises as a nontrivial multivariate generalization of the recently discovered continuous Bernoulli. Unlike the Dirichlet and other typical choices, the continuous categorical results in a well-behaved probabilistic loss function that produces unbiased estimators, while preserving the mathematical simplicity of the Dirichlet. As well as exploring its theoretical properties, we introduce sampling methods for this distribution that are amenable to the reparameterization trick, and evaluate their performance. Lastly, we demonstrate that the continuous categorical outperforms standard choices empirically, across a simulation study, an applied example on multi-party elections, and a neural network compression task.