Computation-Aware Gaussian Processes: Model Selection And Linear-Time Inference

Model selection in Gaussian processes scales prohibitively with the size of the training dataset, both in time and memory. While many approximations exist, all incur inevitable approximation error. Recent work accounts for this error in the form of computational uncertainty, which enables -- at the cost of quadratic complexity -- an explicit tradeoff between computation and precision. Here we extend this development to model selection, which requires significant enhancements to the existing approach, including linear-time scaling in the size of the dataset. We propose a novel training loss for hyperparameter optimization and demonstrate empirically that the resulting method can outperform SGPR, CGGP and SVGP, state-of-the-art methods for GP model selection, on medium to large-scale datasets. Our experiments show that model selection for computation-aware GPs trained on 1.8 million data points can be done within a few hours on a single GPU. As a result of this work, Gaussian processes can be trained on large-scale datasets without significantly compromising their ability to quantify uncertainty -- a fundamental prerequisite for optimal decision-making.

Theoretical Limitations of Ensembles in the Age of Overparameterization

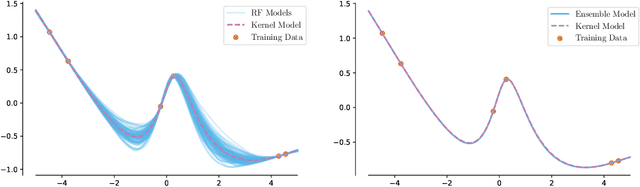
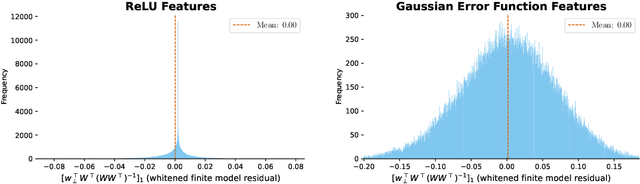
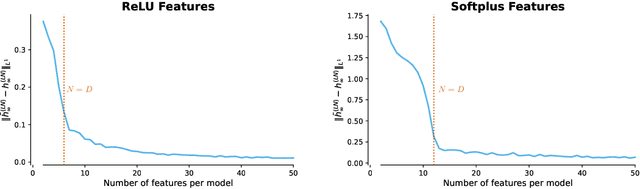
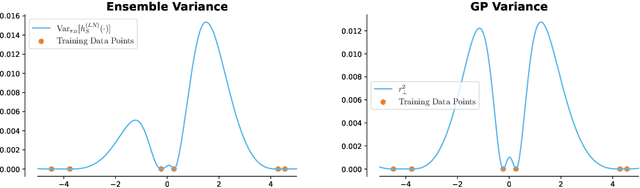
Classic tree-based ensembles generalize better than any single decision tree. In contrast, recent empirical studies find that modern ensembles of (overparameterized) neural networks may not provide any inherent generalization advantage over single but larger neural networks. This paper clarifies how modern overparameterized ensembles differ from their classic underparameterized counterparts, using ensembles of random feature (RF) regressors as a basis for developing theory. In contrast to the underparameterized regime, where ensembling typically induces regularization and increases generalization, we prove that infinite ensembles of overparameterized RF regressors become pointwise equivalent to (single) infinite-width RF regressors. This equivalence, which is exact for ridgeless models and approximate for small ridge penalties, implies that overparameterized ensembles and single large models exhibit nearly identical generalization. As a consequence, we can characterize the predictive variance amongst ensemble members, and demonstrate that it quantifies the expected effects of increasing capacity rather than capturing any conventional notion of uncertainty. Our results challenge common assumptions about the advantages of ensembles in overparameterized settings, prompting a reconsideration of how well intuitions from underparameterized ensembles transfer to deep ensembles and the overparameterized regime.

Estimating the Hallucination Rate of Generative AI

This work is about estimating the hallucination rate for in-context learning (ICL) with Generative AI. In ICL, a conditional generative model (CGM) is prompted with a dataset and asked to make a prediction based on that dataset. The Bayesian interpretation of ICL assumes that the CGM is calculating a posterior predictive distribution over an unknown Bayesian model of a latent parameter and data. With this perspective, we define a \textit{hallucination} as a generated prediction that has low-probability under the true latent parameter. We develop a new method that takes an ICL problem -- that is, a CGM, a dataset, and a prediction question -- and estimates the probability that a CGM will generate a hallucination. Our method only requires generating queries and responses from the model and evaluating its response log probability. We empirically evaluate our method on synthetic regression and natural language ICL tasks using large language models.

Approximation-Aware Bayesian Optimization

High-dimensional Bayesian optimization (BO) tasks such as molecular design often require 10,000 function evaluations before obtaining meaningful results. While methods like sparse variational Gaussian processes (SVGPs) reduce computational requirements in these settings, the underlying approximations result in suboptimal data acquisitions that slow the progress of optimization. In this paper we modify SVGPs to better align with the goals of BO: targeting informed data acquisition rather than global posterior fidelity. Using the framework of utility-calibrated variational inference, we unify GP approximation and data acquisition into a joint optimization problem, thereby ensuring optimal decisions under a limited computational budget. Our approach can be used with any decision-theoretic acquisition function and is compatible with trust region methods like TuRBO. We derive efficient joint objectives for the expected improvement and knowledge gradient acquisition functions in both the standard and batch BO settings. Our approach outperforms standard SVGPs on high-dimensional benchmark tasks in control and molecular design.

LoRA Learns Less and Forgets Less

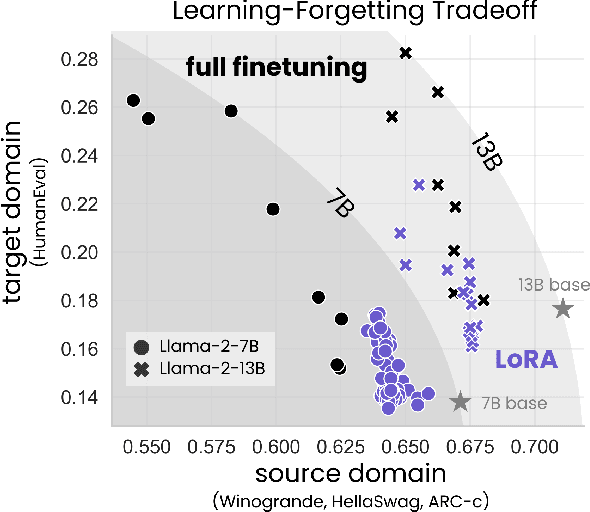
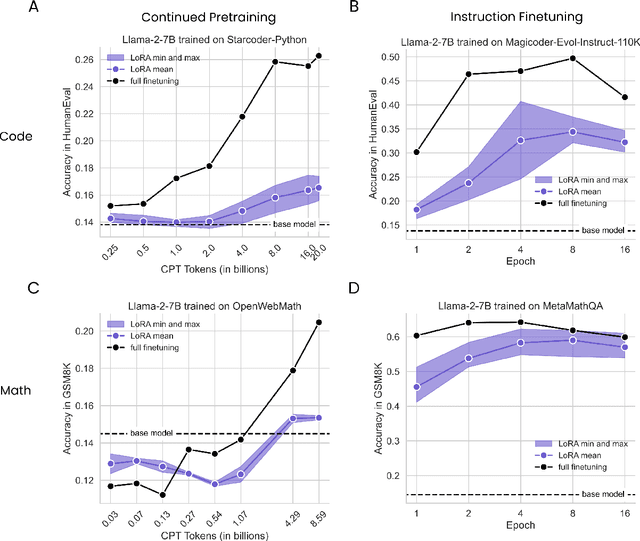
Low-Rank Adaptation (LoRA) is a widely-used parameter-efficient finetuning method for large language models. LoRA saves memory by training only low rank perturbations to selected weight matrices. In this work, we compare the performance of LoRA and full finetuning on two target domains, programming and mathematics. We consider both the instruction finetuning ($\approx$100K prompt-response pairs) and continued pretraining ($\approx$10B unstructured tokens) data regimes. Our results show that, in most settings, LoRA substantially underperforms full finetuning. Nevertheless, LoRA exhibits a desirable form of regularization: it better maintains the base model's performance on tasks outside the target domain. We show that LoRA provides stronger regularization compared to common techniques such as weight decay and dropout; it also helps maintain more diverse generations. We show that full finetuning learns perturbations with a rank that is 10-100X greater than typical LoRA configurations, possibly explaining some of the reported gaps. We conclude by proposing best practices for finetuning with LoRA.

Practical and Asymptotically Exact Conditional Sampling in Diffusion Models

Diffusion models have been successful on a range of conditional generation tasks including molecular design and text-to-image generation. However, these achievements have primarily depended on task-specific conditional training or error-prone heuristic approximations. Ideally, a conditional generation method should provide exact samples for a broad range of conditional distributions without requiring task-specific training. To this end, we introduce the Twisted Diffusion Sampler, or TDS. TDS is a sequential Monte Carlo (SMC) algorithm that targets the conditional distributions of diffusion models. The main idea is to use twisting, an SMC technique that enjoys good computational efficiency, to incorporate heuristic approximations without compromising asymptotic exactness. We first find in simulation and on MNIST image inpainting and class-conditional generation tasks that TDS provides a computational statistical trade-off, yielding more accurate approximations with many particles but with empirical improvements over heuristics with as few as two particles. We then turn to motif-scaffolding, a core task in protein design, using a TDS extension to Riemannian diffusion models. On benchmark test cases, TDS allows flexible conditioning criteria and often outperforms the state of the art.

Pathologies of Predictive Diversity in Deep Ensembles

Classical results establish that ensembles of small models benefit when predictive diversity is encouraged, through bagging, boosting, and similar. Here we demonstrate that this intuition does not carry over to ensembles of deep neural networks used for classification, and in fact the opposite can be true. Unlike regression models or small (unconfident) classifiers, predictions from large (confident) neural networks concentrate in vertices of the probability simplex. Thus, decorrelating these points necessarily moves the ensemble prediction away from vertices, harming confidence and moving points across decision boundaries. Through large scale experiments, we demonstrate that diversity-encouraging regularizers hurt the performance of high-capacity deep ensembles used for classification. Even more surprisingly, discouraging predictive diversity can be beneficial. Together this work strongly suggests that the best strategy for deep ensembles is utilizing more accurate, but likely less diverse, component models.

Posterior Collapse and Latent Variable Non-identifiability

Variational autoencoders model high-dimensional data by positing low-dimensional latent variables that are mapped through a flexible distribution parametrized by a neural network. Unfortunately, variational autoencoders often suffer from posterior collapse: the posterior of the latent variables is equal to its prior, rendering the variational autoencoder useless as a means to produce meaningful representations. Existing approaches to posterior collapse often attribute it to the use of neural networks or optimization issues due to variational approximation. In this paper, we consider posterior collapse as a problem of latent variable non-identifiability. We prove that the posterior collapses if and only if the latent variables are non-identifiable in the generative model. This fact implies that posterior collapse is not a phenomenon specific to the use of flexible distributions or approximate inference. Rather, it can occur in classical probabilistic models even with exact inference, which we also demonstrate. Based on these results, we propose a class of latent-identifiable variational autoencoders, deep generative models which enforce identifiability without sacrificing flexibility. This model class resolves the problem of latent variable non-identifiability by leveraging bijective Brenier maps and parameterizing them with input convex neural networks, without special variational inference objectives or optimization tricks. Across synthetic and real datasets, latent-identifiable variational autoencoders outperform existing methods in mitigating posterior collapse and providing meaningful representations of the data.

Denoising Deep Generative Models

Likelihood-based deep generative models have recently been shown to exhibit pathological behaviour under the manifold hypothesis as a consequence of using high-dimensional densities to model data with low-dimensional structure. In this paper we propose two methodologies aimed at addressing this problem. Both are based on adding Gaussian noise to the data to remove the dimensionality mismatch during training, and both provide a denoising mechanism whose goal is to sample from the model as though no noise had been added to the data. Our first approach is based on Tweedie's formula, and the second on models which take the variance of added noise as a conditional input. We show that surprisingly, while well motivated, these approaches only sporadically improve performance over not adding noise, and that other methods of addressing the dimensionality mismatch are more empirically adequate.

Posterior and Computational Uncertainty in Gaussian Processes

Gaussian processes scale prohibitively with the size of the dataset. In response, many approximation methods have been developed, which inevitably introduce approximation error. This additional source of uncertainty, due to limited computation, is entirely ignored when using the approximate posterior. Therefore in practice, GP models are often as much about the approximation method as they are about the data. Here, we develop a new class of methods that provides consistent estimation of the combined uncertainty arising from both the finite number of data observed and the finite amount of computation expended. The most common GP approximations map to an instance in this class, such as methods based on the Cholesky factorization, conjugate gradients, and inducing points. For any method in this class, we prove (i) convergence of its posterior mean in the associated RKHS, (ii) decomposability of its combined posterior covariance into mathematical and computational covariances, and (iii) that the combined variance is a tight worst-case bound for the squared error between the method's posterior mean and the latent function. Finally, we empirically demonstrate the consequences of ignoring computational uncertainty and show how implicitly modeling it improves generalization performance on benchmark datasets.